Subsections
Modulação de impulsos
Introdução
Hoje em dia a maior parte da informação encontra-se sob forma discreta, apesar de parte dessa informação ser na origem analógica ela é discretizada e quantificada na fonte. Como exemplos podemos citar a voz no caso do telefone, a música, a imagem, etc...O mais curioso é que quer a informação já discreta na origem quer a analógica discretizada devem ser adaptadas ao canal de transmissão que, ele, é essencialmente analógico por natureza. Este processo de adaptação ao canal de transmissão é chamado modulação. Já vimos exemplos de modulação analógica no capítulo 5.
Começaremos por descrever a técnica de base, de longe a mais utilizada hoje em dia, que é a modulação de impulsos (pulse modulation -PM). Nesta técnica uma série de impulsos emitidos a uma determinada cadência modulam uma sequência de símbolos que constituem ''uma imagem'' da mensagem a transmitir. De uma forma geral trata-se de associar os k
mathend000# digitos binários à saída do codificador a M = 2k
mathend000# sinais (ou níveis) possíveis. Esta é chamada a fase de mapeamento (ou sinalização), durante a qual cada um dos M
mathend000# níveis se encontra associado a um sinal sm(t)
mathend000# de um conjunto de
{sm(t);m = 1,..., M}
mathend000# sinais possíveis. Apesar de, teoricamente, cada um dos sinais sm(t)
mathend000# poder ter qualquer forma, na prática, por questões de facilidade de implementação a família de sinais é escolhida como uma variante de uma forma de base, que é normalmente chamada ``forma de pulso'' ou pulse shape. A escolha da ``forma de pulso'' depende essencialmente de dois factores:
- do espectro desejado para o sinal a emitir no meio físico, porque é ele que vai ser determinante na ocupação do espectro de frequências disponíveis para uma dada transmissão;
- da capacidade de ser distinguindo no receptor minimizando assim a probabilidade de erro no decisor.
A técnica de PM será primeiramente descrita em banda base, i.e., numa banda de frequências que inclui a componente contínua (zero Hz). Em seguida falaremos do caso em banda passante onde o sinal PM ele próprio modulará uma portadora sinusoidal (caso análogo ao caso da modulação analógica).
Generalidades
Retomemos o esquema de blocos de um sistema de comunicações da figura 1.1, mas com um maior detalhe interno de cada um dos três grandes blocos - figura 7.1.
Figura 7.1:
sistema de transmissão em banda base.
|
|
Nos dois sub-blocos do transmissor - o codificador e o filtro de transmissão - encontra-se agora a sequência de bits de entrada Bn
mathend000# que é aplicada ao codificador e onde é, por sua vez, transformada numa sequência de símbolos Ak
mathend000# de saída. A sequência de bits pode assumir os valores `0' ou `1' enquanto a sequência de símbolos pode tomar qualquer valor de um alfabeto escolhido. Uma das características principais do codificador é de que a relação entre Bn
mathend000# e Ak
mathend000# pode não ser de um para um. Isto significa que dois bits diferentes podem ser representados pelo mesmo símbolo e inversamente podem existir símbolos que não correspondem a nenhum dos bits de entrada. É por essa razão que a taxa de transmissão da sequência de bits é simbolizada pelo índice n
mathend000# e chamada taxa de bit (ou bit rate) Rb = 1/Tb
mathend000# (Tb
mathend000# é o intervalo de amostagem da sequência de bits) e a taxa de transmissão dos símbolos é simbolizada pelo índice k
mathend000# e é chamada taxa de símbolo (ou symbol rate) Rs = 1/Ts
mathend000# (onde Ts
mathend000# é o intervalo de amostragem da sequência de símbolos). Na prática os dois casos
1/Tb > 1/Ts
mathend000# ou
1/Tb < 1/Ts
mathend000# são possíveis. Normalmente se a taxa de bit for superior à taxa de símbolo dizemos que há compressão, no caso contrário dizemos que existe redundância. Neste capítulo assumiremos que não existe nem redundância nem compressão, que Rb = Rs
mathend000# e que os símbolos saídos do codificador são independentes e idênticamente distribuidos formando um processo aleatório branco.
O segundo sub-bloco do transmissor é o filtro de transmissão ou modulador que tem por papel o de receber à entrada uma sequência de símbolos discretos e gerar à saída um sinal analógico - sinal modulado. A primeira etapa da modulação consiste em atribuir um nível
{Am;m = 1,..., M}
mathend000# a cada símbolo do alfabeto de dimensão M
mathend000#. Em seguida, cada um dos símbolos possíveis é colocado à entrada do filtro de saída do modulador e encontra-se à saída convoluido pela resposta impulsiva deste, seja g(t)
mathend000#,
s(t) = 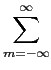 Amg(t - mTs), Amg(t - mTs), |
(7-2.01) |
onde Ts
mathend000# é o período de símbolo e g(t)
mathend000# é a ``forma de pulso''. Finalmente, a última etapa consiste em deslocar o sinal resultante na frequência portadora do canal de transmissão, seja fc
mathend000# Hz (não representado na figura 7.1). Todo este processo pode ser visto como o de atribuir um sinal sm(t)
mathend000# em banda, a cada símbolo do alfabeto e é por isso chamada etapa de sinalização.
Como já foi referido no capítulo 3, o canal de transmissão pode ser considerado em muitos casos práticos, como sendo representado por um filtro linear invariante, cuja resposta impulsiva é b(t)
mathend000# e o ruído de observação n(t)
mathend000# é considerado do tipo aditivo. Assim o sinal à saída do canal, ou à entrada do receptor, é dado por
r(t) =  b( b( ) )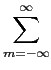 Amg(t - mTs - Amg(t - mTs -  )d )d + n(t). + n(t). |
(7-2.02) |
Esta equação pode ser rescrita como
r(t) = 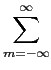 Amh(t - mTs) + n(t), Amh(t - mTs) + n(t), |
(7-2.03) |
onde
| h(t) = b(t) * g(t), |
(7-2.04) |
é chamado o impulso recebido, i.e., a ``forma de pulso'' depois de filtrada pelo canal de transmissão.
O terceiro bloco da figura 7.1 é o receptor. O receptor recebe à entrada um sinal contínuo r(t)
mathend000# que é, num sistema real, antes do mais colocado em banda base (não representado na figura). O primeiro sub-bloco do receptor é o filtro de recepção, designado pela sua resposta impulsiva f (t)
mathend000#. Este filtro de recepção é um dos componentes mais importantes e também, frequentemente, um dos mais complexos de todo o sistema de comunicações. É importante que este filtro esteja perfeitamente sintonizado com o filtro do emissor por um lado e com o tipo de canal de transmissão por outro. O sinal q(t)
mathend000# à saída do filtro receptor escreve-se,
| q(t) |
= |
f (t) * r(t) |
|
| |
= |
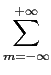 Amp(t - mTs) + u(t), Amp(t - mTs) + u(t), |
(7-2.05) |
onde
p(t) = f (t) * b(t) * g(t)
mathend000# e o ruído
u(t) = f (t) * n(t)
mathend000#. Não é difícil perceber que para que o sinal q(t)
mathend000# tome o valor do símbolo Ak
mathend000# no instante t = kTs
mathend000# é preciso que
q(kTs) = 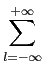 Amp[(k - m)Ts] + u(kTs) Amp[(k - m)Ts] + u(kTs) |
(7-2.06) |
seja igual a Ak
mathend000#, que só é possível se: 1)
p[(k - m)Ts] = 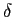 (k - m)
mathend000# e 2) que u(kTs) = 0
mathend000#. A escolha dos vários blocos do sistema de forma a respeitar estas duas condições é o tema do capítulo 7.4. A seguir ao sub-bloco do filtro receptor encontra-se um amostrador que deve ser pilotado a uma cadência síncrona com o intervalo de símbolo Ts
mathend000#, o que por vezes coloca algumas dificuldades na prática quando o emissor e o receptor se encontram a grande distância um do outro e/ou são muito diferentes entre si. O sub-bloco a seguir é o decisor que na prática identifica o valor qk
mathend000# à sua entrada com o símbolo estimado correspondente
(k - m)
mathend000# e 2) que u(kTs) = 0
mathend000#. A escolha dos vários blocos do sistema de forma a respeitar estas duas condições é o tema do capítulo 7.4. A seguir ao sub-bloco do filtro receptor encontra-se um amostrador que deve ser pilotado a uma cadência síncrona com o intervalo de símbolo Ts
mathend000#, o que por vezes coloca algumas dificuldades na prática quando o emissor e o receptor se encontram a grande distância um do outro e/ou são muito diferentes entre si. O sub-bloco a seguir é o decisor que na prática identifica o valor qk
mathend000# à sua entrada com o símbolo estimado correspondente 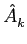 mathend000# entre os possíveis
{Am;m = 1,..., M}
mathend000# à sua saída. Finalmente, o último sub-bloco é o descodificador que, através da operação inversa realizada no emissor, recebe à entrada o stream de símbolos estimados
mathend000# entre os possíveis
{Am;m = 1,..., M}
mathend000# à sua saída. Finalmente, o último sub-bloco é o descodificador que, através da operação inversa realizada no emissor, recebe à entrada o stream de símbolos estimados 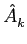 mathend000# e produz à saída o stream de bits estimado
mathend000# e produz à saída o stream de bits estimado 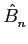 mathend000#.
mathend000#.
Medidas de desempenho
Como já tivemos a ocasião de referir uma das medidas de desempenho de um determinado sistema de comunicação é a taxa de bit (ou bit rate) que permite realizar num determinado canal de transmissão. Assim é, por exemplo, frequente referir que um determinado modem tem uma taxa de transmissão de 1200, 2400 ou 9600 bits/s. Obviamente quando mais elevada é a bit rate, maior é o desempenho, apesar de não ser referida a taxa de erro obtida para este desempenho. Pressupõe-se que esta seja suficientemente baixa, o que é subjectivo. Os erros de detecção podem ser tornados arbitrariamente baixos aumentando a complexidade do emissor/receptor. Evitaremos entrar neste campo de compromisso entre bit rate versus complexidade.
Outra medida de desempenho normalmente aceite é definida pela bit rate por largura de banda. Noutras palavras, uma bit rate mais alta requer uma banda mais larga, portanto um sistema será tanto mais eficiente quanto maior for a sua, chamada, eficiência espectral dada por
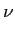 = = 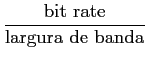 , , |
(7-3.01) |
que se mede em bits/s/Hz.
Por exemplo, um sistema com um alfabeto
{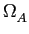 }
mathend000# de dimensão,
|
}
mathend000# de dimensão,
|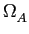 |
mathend000# admite uma taxa de transmissão de
log2|
|
mathend000# admite uma taxa de transmissão de
log2|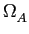 |
mathend000# bits por cada símbolo, no caso simples em que existe uma relação um para um entre grupos de bits e cada símbolo. Assim, a bit rate será, neste caso, dada por
log2|
|
mathend000# bits por cada símbolo, no caso simples em que existe uma relação um para um entre grupos de bits e cada símbolo. Assim, a bit rate será, neste caso, dada por
log2|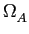 |/Ts
mathend000# (1/Ts
mathend000# é a symbol rate) e por isso a eficiência espectral escreve-se
|/Ts
mathend000# (1/Ts
mathend000# é a symbol rate) e por isso a eficiência espectral escreve-se
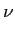 = = 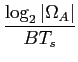 , , |
|
onde B
mathend000# é a largura de banda em Hz.
Portanto, e em resumo, a symbol rate encontra-se limitada na prática pela largura de banda do canal de transmissão. Como demonstraremos mais adiante, se quisermos evitar completamente a interferência intersimbólica a symbol rate poderá ser no máximo o dobro da largura de banda do canal. Por outro lado, a dimensão do alfabeto encontra-se limitada pela potência máxima transmissível e pelo nível de ruído no canal. Estas duas limitações, na symbol rate e na dimensão do alfabeto, é que restringem efectivamente a bit rate alcançavel num determinado sistema de transmissão.
Escolha da forma de pulso
Densidade espectral do sinal emitido
No capítulo 7.2 falámos, quando da equação (7-2.1), na função g(t)
mathend000# à qual chamámos forma de pulso (pulse shape). A escolha da forma de pulso permite uma melhor adaptação às características do canal de transmissão. Como já tivemos a ocasião de referir, a sequência de símbolos Ak
mathend000# pode ser, numa primeira aproximação, considerada estacionária e de variância
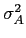 = E[|A
= E[|A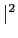 ]
mathend000#.
]
mathend000#.
Comecemos por notar que podemos designar um sinal de tipo passabanda modulado em torno à frequência fc
mathend000# como
s(t) = Re[sbb(t)ej2 fct], fct], |
(7-4.01) |
onde sbb(t)
mathend000# é o sinal passa-baixo de s(t)
mathend000# que, para as modulações lineares introduzidas acima, se escreve
sbb(t) = 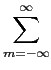 Amg(t - mTs). Amg(t - mTs). |
(7-4.02) |
onde Ts
mathend000# é o intervalo de símbolo. De notar que para este tipo de modulações Am
mathend000# é real e contém a informação da mensagem no caso ASK, e é complexo no caso PSK, QAM, e ASK-PSK (ver mais à frente). Em qualquer dos casos a sequência
{Am, m = 1,..., M}
mathend000# é aleatória e portanto sbb(t)
mathend000# e s(t)
mathend000# são eles mesmos processos aleatórios. O primeiro passo no cálculo da densidade espectral de potência é estimar a função de autocorrelação, que para o caso do sinal (7-4.1) se escreve
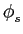 ( ( ) = Re[ ) = Re[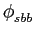 ( ( )ej2 )ej2 fct], fct], |
(7-4.03) |
onde
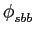 (
( )
mathend000# é a função de autocorrelação do componente passa-baixo sbb(t)
mathend000#. A TF de (7-4.3) permite obter a densidade espectral de potência
)
mathend000# é a função de autocorrelação do componente passa-baixo sbb(t)
mathend000#. A TF de (7-4.3) permite obter a densidade espectral de potência
| Ps(f ) |
= |
TF[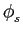 ( ( )], )], |
|
| |
= |
 [Psbb(f - fc) + Psbb(f + fc)], [Psbb(f - fc) + Psbb(f + fc)], |
(7-4.04) |
onde se utilizou explicitamente a expressão (2-2.44). Trata-se agora de determinar a expressão da densidade espectral de potência da componente passa-baixo
Psbb(f )
mathend000#. A função de autocorrelação de sbb(t)
mathend000# escreve-se
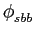 (t + (t +  , t) = E[sbb(t + , t) = E[sbb(t +  )sbb * (t)], )sbb * (t)], |
(7-4.05) |
e por substituição de (7-4.2) em (7-4.5) obtemos
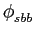 (t + (t +  , t) = , t) = 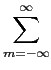 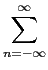 E[AmA * n]g(t + E[AmA * n]g(t +  - mTs)g * (t - nTs). - mTs)g * (t - nTs). |
(7-4.06) |
Assumindo que a mensagem é uma sequência de bits/símbolos estacionária de média 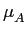 mathend000# e de função de autocorrelação
mathend000# e de função de autocorrelação
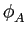 (m - n) = E[AmA * n], (m - n) = E[AmA * n], |
(7-4.07) |
então podemos escrever (7-4.6) como
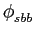 (t + (t +  , t) = , t) = 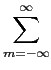 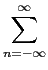 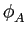 (m - n)g(t + (m - n)g(t +  - mTs)g * (t - nTs), - mTs)g * (t - nTs), |
(7-4.08) |
e fazendo uma mudança de variável i = m - n
mathend000#, obtemos
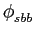 (t + (t +  , t) = , t) = 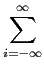 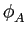 (i) (i)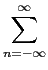 g(t + g(t +  - iT - nTs)g * (t - nTs), - iT - nTs)g * (t - nTs), |
(7-4.09) |
a partir da qual é agora fácil determinar que
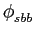 (t + (t +  , t) = , t) = 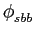 (t + Ts + (t + Ts +  , t + Ts), , t + Ts), |
(7-4.10) |
dado que o facto de adicionar Ts
mathend000# ao tempo t
mathend000# apenas adiciona mais um termo em n
mathend000#, mas como este varia no intervalo
[- 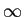 , +
, + 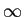 ]
mathend000#, o valor da expressão não é alterado. Assim
]
mathend000#, o valor da expressão não é alterado. Assim
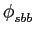 (t +
(t +  , t)
mathend000# é uma função periódica, de período igual ao intervalo de símbolo Ts
mathend000#. Dado que a média do processo s(t)
mathend000# é dada por
, t)
mathend000# é uma função periódica, de período igual ao intervalo de símbolo Ts
mathend000#. Dado que a média do processo s(t)
mathend000# é dada por
E[s(t)] = 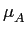 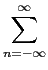 g(t - nTs) g(t - nTs) |
(7-4.11) |
também periódica de mesmo período Ts
mathend000# chegamos à conclusão que o processo estocástico s(t)
mathend000# se enquadra na definição de um processo periodicamente estacionário no sentido lato ou cicloestacionário definida no capítulo 2.4. Como tivemos ocasião de referir, o cálculo do espectro dos sinais cicloestacionários faz-se através da TF da média temporal da função de autocorrelação do processo num período. Essa média temporal escreve-se neste caso como
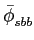 ( ( ) = ) = 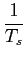 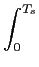 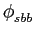 (t + (t +  , t)dt, , t)dt, |
(7-4.12) |
e assim, substituindo (7-4.9) em (7-4.12) com a mudança de variável u = t - nTs
mathend000#, o que implica que quando t = 0
mathend000#, u = - nTs
mathend000# e para t = Ts
mathend000#,
u = - (n - 1)Ts
mathend000# temos
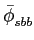 ( ( ) = ) = 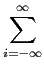 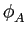 (i) (i)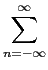 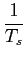 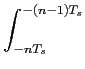 g(u + g(u +  - iTs)g * (u)du. - iTs)g * (u)du. |
(7-4.13) |
O integral é feito num intervalo Ts
mathend000# e depois somado com todos os outros intervalos para
t 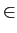 ] -
] - 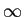 ,
,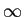 [
mathend000# de acordo com os valores de n
mathend000#. No entanto a funçã g(t)
mathend000# só é diferente de zero num dos intervalos Ts
mathend000# e por isso o resultado da combinação do somatório em n
mathend000# e do integral num único intervalo pode ser representado por um único integral num intervalo infinito, assim podemos escrever
[
mathend000# de acordo com os valores de n
mathend000#. No entanto a funçã g(t)
mathend000# só é diferente de zero num dos intervalos Ts
mathend000# e por isso o resultado da combinação do somatório em n
mathend000# e do integral num único intervalo pode ser representado por um único integral num intervalo infinito, assim podemos escrever
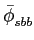 ( ( ) = ) = 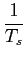 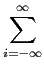 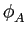 (i) (i) g(u + g(u +  - iTs)g * (u)du, - iTs)g * (u)du, |
(7-4.14) |
e finalmente
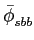 ( ( ) = ) = 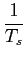 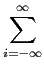 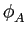 (i) (i)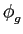 ( ( - iTs), - iTs), |
(7-4.15) |
onde
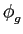 ( ( ) = ) =  g(t + g(t +  )g * (t)dt. )g * (t)dt. |
(7-4.16) |
Escrevendo finalmente o espectro de potência de sbb(t)
mathend000# como a TF de
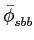 (
( )
mathend000#, i.e.,
)
mathend000#, i.e.,
Psbb(f )=  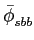 ( ( )e-j2 )e-j2 f f d d , , |
(7-4.17) |
e notando que (7-4.15) representa apenas a convolução das autocorrelações de Ak
mathend000# e da função de pulso g(t)
mathend000#, permite chegar a
Psbb(f )= 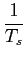 |G(f ) |G(f ) PA(f ). PA(f ). |
(7-4.18) |
Na prática somos levados a determinar g(t)
mathend000# de forma a que o seu espectro se adapte ao canal de transmissão ou, alternativamente, tendo em conta (7-4.18), controlando as propriedades da função de autocorrelação 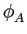 (i)
mathend000# da sequência de bits transmitida. Com efeito podemos determinar a densidade espectral de
(i)
mathend000# da sequência de bits transmitida. Com efeito podemos determinar a densidade espectral de 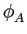 (i)
mathend000# através da TF
(i)
mathend000# através da TF
PA(f )= 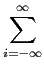 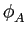 (i)e-j2 (i)e-j2 fiTs, fiTs, |
(7-4.19) |
e inversamente
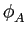 (i) = (i) = 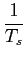 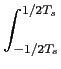 PA(f )ej2 PA(f )ej2 fiTsdf, fiTsdf, |
(7-4.20) |
Considerando, por exemplo, que os bits/símbolos de informação são reais de média
E[Am] = 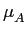 mathend000# e descorrelacionados (branco) com variância
V[Am] =
mathend000# e descorrelacionados (branco) com variância
V[Am] = 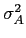 mathend000# teremos que a função de autocorrelação
mathend000# teremos que a função de autocorrelação
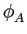 (i) = E[Am+iAm * ]
mathend000# se escreve
(i) = E[Am+iAm * ]
mathend000# se escreve
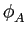 (i) = (i) = 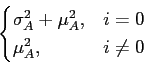 |
(7-4.21) |
Substituindo (7-4.21) em (7-4.19) obtemos
PA(f )= 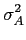 + + 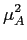 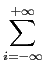 e-j2 e-j2 fiTs. fiTs. |
(7-4.22) |
O somatório do segundo termo representa a TF discreta no tempo de um sinal discreto x[i] = 1
mathend000#. O resultado é obviamente um Dirac no domínio da frequência mas que vai ser periódico (porque o sinal é discreto no tempo) de período 1/Ts
mathend000# (ver sebenta de Sinais e Sistemas [5]),
PA(f )= 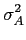 + + 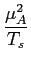 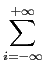 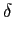 (f - i/Ts), (f - i/Ts), |
(7-4.23) |
e finalmente a substituição da densidade espectral da sequência de informação PA(f )
mathend000# na expressão da densidade espectral do sinal passa-baixo (7-4.18) permite escrever
Psbb(f )= 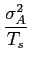 |G(f ) |G(f ) + + 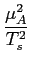 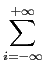 |G(i/Ts) |G(i/Ts) 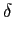 (f - i/Ts). (f - i/Ts). |
(7-4.24) |
É interessante constatar que os dois termos desta expressão po m em relevo dois tipos de componentes espectrais: 1) o primeiro termo é um espectro contínuo e depende unicamente do espectro da ``forma do pulso'' g(t)
mathend000# e 2) o segundo termo é formado por uma série infinita de componentes espectrais espaçadas de 1/Ts
mathend000# cuja amplitude é igual ao espectro da função de pulso G(f )
mathend000# nos pontos i/Ts
mathend000#. De notar que no caso
m em relevo dois tipos de componentes espectrais: 1) o primeiro termo é um espectro contínuo e depende unicamente do espectro da ``forma do pulso'' g(t)
mathend000# e 2) o segundo termo é formado por uma série infinita de componentes espectrais espaçadas de 1/Ts
mathend000# cuja amplitude é igual ao espectro da função de pulso G(f )
mathend000# nos pontos i/Ts
mathend000#. De notar que no caso 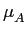 = 0
mathend000# temos apenas
= 0
mathend000# temos apenas
Psbb(f )= 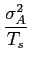 |G(f ) |G(f ) , , |
(7-4.25) |
de onde podemos concluir que, neste caso, o espectro do sinal a transmitir se torna independente da mensagem dependendo apenas do espectro da função de pulso g(t)
mathend000#.
Exemplo 1: considere a ``forma de pulso'' representada na figura 7.2a, e definida por
Figura:
``forma de pulso'' rectangular causal de duração T = 5
mathend000# ms (a) e respectivo espectro de potência
|G(f )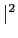 mathend000# (b).
mathend000# (b).
| (a) |
(b) |
![\includegraphics[width=7cm]{figs/square_pulse.eps}](img375.png) |
![\includegraphics[width=7cm]{figs/spec_square_pulse.eps}](img376.png) |
|
g(t) = ![\begin{displaymath}\begin{cases}
0 & t \in [-\infty,0[ \\ A & t \in [0,T] \\ 0 & t \in ]T,\infty[ \end{cases}\end{displaymath}](img377.png) |
|
Calcule o seu espectro de potência
|G(f )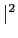 mathend000#.
mathend000#.
Trata-se de um cálculo clássico, que se pode fazer como exercício de revisão da TF, assim temos que
| G(f ) |
= |
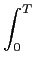 Ae-j2 Ae-j2 ftdt, ftdt, |
|
| |
= |
A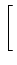 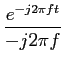 ![$\displaystyle \left.\vphantom{{{e^{-j2\pi ft}}\over {-j2\pi f}}}\right]_{0}^{T}$](img381.png) |
|
| |
= |
A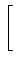 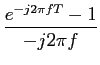 ![$\displaystyle \left.\vphantom{{{e^{-j2\pi fT} - 1}\over {-j2\pi f}}}\right]$](img384.png) |
|
| |
= |
Ae-j fT fT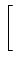 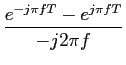 ![$\displaystyle \left.\vphantom{{{e^{-j\pi fT} - e^{j\pi fT}}\over {-j2\pi f}}}\right]$](img387.png) |
|
| |
= |
Ae-j fT fT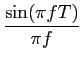 , , |
|
ou ainda
G(f )= AT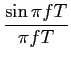 e-j e-j fT, fT, |
|
e finalmente
espectro que se encontra representado na figura 7.2b.
Figura:
``forma de pulso'' raised cosine de duração T = 5
mathend000# ms (a) e respectivo espectro de potência
|G(f )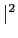 mathend000# (b).
mathend000# (b).
| (a) |
(b) |
![\includegraphics[width=7cm]{figs/rc_pulse.eps}](img392.png) |
![\includegraphics[width=7cm]{figs/spec_rc_pulse.eps}](img393.png) |
|
Exemplo 2: outra ``forma de pulso'' tipicamente utilizada em comunicações é o coseno elevado (raised cosine) dado pela expressão
g(t) = ![\begin{displaymath}\begin{cases}
{A\over 2}\left[ 1 + \cos {{2\pi}\over T}(t-{T\...
...2})\right], & 0 \le t \le T \\ 0 & t \not\in [0,T], \end{cases}\end{displaymath}](img394.png) |
|
e representada na figura 7.3a. O cálculo do seu espectro de potência passa obviamente pela TF de g(t)
mathend000#. O cálculo é algo semelhante ao do exemplo anterior porém muito mais trabalhoso. Após algumas páginas de cálculo podemos chegar ao resultado notável
sendo o seu espectro de potência
que se encontra representado na figura 7.3b. Comparando com o espectro de potência da ``forma de pulso'' rectangular pode-se notar que também aqui os nulos são obtidos para múltiplos do inverso da duração do pulso n/T
mathend000#, porém contrariamente ao caso do pulso rectangular o primeiro zero não se obtem para n = 1
mathend000# mas só a partir de n = 2
mathend000#, indiciando uma largura do lóbulo principal muito maior do que no caso do pulso rectangular. Em compensação, a curva de decaimento do lóbulo central do espectro de potência é muito mais rápida do que no caso do pulso rectangular.
Como exemplo de escola podemos referir que se o canal de transmissão for um canal passa-baixo ideal, dado por
B(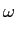 ) = ) = 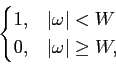 |
(7-4.26) |
então o espectro da função de pulso é
G(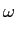 ) = ) = 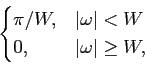 |
(7-4.27) |
que no domínio do tempo é uma função sinc,
g(t) = 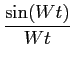 . . |
(7-4.28) |
Dado que esta função tem as suas passagens por zero para múltiplos de 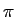 /W
mathend000# poderemos escolher a duração de cada símbolo como Ts =
/W
mathend000# poderemos escolher a duração de cada símbolo como Ts = 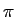 /W
mathend000#. Esta taxa de símbolo de 1/Ts
mathend000# é o valor máximo (e por isso óptimo) que pode ser obtido para um canal de largura de banda W
mathend000#. Infelizmente, sinais de banda limitada como o descrito em (7-4.27) não são realizáveis na prática e somos por isso relegados para o problema do desenho de uma forma de pulso que seja por um lado realizável e por outro que maximize a taxa de símbolo para uma dada banda W
mathend000#.
/W
mathend000#. Esta taxa de símbolo de 1/Ts
mathend000# é o valor máximo (e por isso óptimo) que pode ser obtido para um canal de largura de banda W
mathend000#. Infelizmente, sinais de banda limitada como o descrito em (7-4.27) não são realizáveis na prática e somos por isso relegados para o problema do desenho de uma forma de pulso que seja por um lado realizável e por outro que maximize a taxa de símbolo para uma dada banda W
mathend000#.
Interferência intersimbólica
Na prática o valor mínimo da largura de banda W = 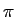 /Ts
mathend000# do ``pulso'' é sempre excedido de forma a simplificar a implementação. Este aumento da largura de banda da forma do impulso é chamado excesso de banda e varia geralmente entre 10 e 100%. Por exemplo um excesso de banda de 100% corresponde a uma largura de banda de 2
/Ts
mathend000# do ``pulso'' é sempre excedido de forma a simplificar a implementação. Este aumento da largura de banda da forma do impulso é chamado excesso de banda e varia geralmente entre 10 e 100%. Por exemplo um excesso de banda de 100% corresponde a uma largura de banda de 2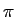 /Ts
mathend000#. Para obter um excesso de banda igual a zero e uma interferência intersimbólica (Intersymbol Interference - ISI) também igual a zero, a forma do impulso é única e é dada pelo sinc, porém para um excesso de banda não nulo existem várias formas de pulso possíveis e por isso trata-se agora de selecionar aquelas que tem ISI nula. O critério de seleção que permite determinar as formas de pulso com ISI nula chama-se critério de Nyquist.
/Ts
mathend000#. Para obter um excesso de banda igual a zero e uma interferência intersimbólica (Intersymbol Interference - ISI) também igual a zero, a forma do impulso é única e é dada pelo sinc, porém para um excesso de banda não nulo existem várias formas de pulso possíveis e por isso trata-se agora de selecionar aquelas que tem ISI nula. O critério de seleção que permite determinar as formas de pulso com ISI nula chama-se critério de Nyquist.
O sinal de saída do filtro de recepção é dado por (7-2.5) e o sinal amostrado dado no instante kTs
mathend000# por (7-2.6). Podemos assim escrever
Qk = Akp(0) + 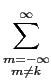 Amp(kTs - mTs) + u(kTs), Amp(kTs - mTs) + u(kTs), |
(7-4.29) |
Olhando atentamente para esta expressão podemos notar que uma recepção sem erros implicaria simplesmente Qk = Ak
mathend000#. Todo o resto desta expressão significa uma parte indesejável no resultado. É obviamente o caso do ruído u(t)
mathend000# e do segundo termo da expressão (7-4.29). Este segundo termo é chamado interferência intersimbólica ou ISI. Uma forma de anular a ISI seria fazer com que o sinal p(t)
mathend000# passasse em zero para todos os valores de t
mathend000# múltiplos de Ts
mathend000#, i.e.,
p(kTs) = 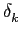 , , |
(7-4.30) |
e portanto (7-4.29) se escrevesse
Qk = 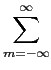 Am Am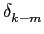 + uk = Ak + uk. + uk = Ak + uk. |
(7-4.31) |
A esta forma de anular a ISI chama-se critério de ''zero-forcing''. Este critério não é de forma nenhuma óptimo pois é puramente determinístico e não tem em conta o ruído. O problema agora é de, a partir do critério de ''zero-forcing'', estabelecer uma relação que permita desenhar a forma de pulso g(t)
mathend000#. Tomando a TF de (7-4.30) onde substituimos a função p(kTs)
mathend000# pela função discreta p(t)
mathend000# multiplicada pela função de amostragem (sequência de Diracs) e dizemos que deverá ser igual a 1 no domínio da frequência
TF[p(kTs)] = TF[p(t)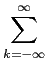 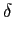 (t - kTs)] = 1. (t - kTs)] = 1. |
(7-4.32) |
Sabendo que a TF do produto é a convolução das TF's e que a TF de um pente de Diracs no tempo é um pente de Diracs na frequência (ver de novo o texto de apoio de Sinais e Sistemas [5]),
P(f ) * 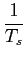 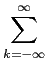  (f - (f - 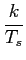 ) = 1, ) = 1, |
(7-4.33) |
e finalmente resolvendo o produto de convolução
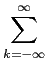 P(f - P(f - 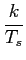 ) = Ts. ) = Ts. |
(7-4.34) |
A equação (7-4.34) é chamada critério de Nyquist para ISI igual a zero5. Vamos agora supôr que o canal de transmissão B(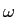 )
mathend000# é tal que
B(
)
mathend000# é tal que
B(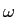 ) = 0
mathend000# para
|
) = 0
mathend000# para
|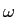 |> W
mathend000#. Temos assim os três casos possíveis exemplificados na figura 7.4:
|> W
mathend000#. Temos assim os três casos possíveis exemplificados na figura 7.4:
Figura 7.4:
critério de ``zero forcing'' com um espectro arbitrário de P(f )
mathend000# de largura 2W
mathend000# que se repete periodicamente com período 1/Ts
mathend000#: para 1/Ts > 2W
mathend000# (a), para 1/Ts = 2W
mathend000# (b) e para
1/Ts > 2W
mathend000# (c).
|
|
- 1)
- Ts < 1/2W
mathend000# ou de forma equivalente
1/Ts > 2W
mathend000#. Neste caso o sinal somatório do lado esquerdo da expressão (7-4.34) é uma sequência de espectros disjuntos e não sobrepostos. Neste caso torna-se impossível verificar a equação (7-4.34) dado que há zonas do espectro `vazias' de tal forma que não existe nenhum sinal p(t)
mathend000# tal que a soma do seu espectro P(f )
mathend000# possa fazer uma constante Ts
mathend000#.
- 2)
- Ts = 1/2W
mathend000# ou
1/Ts = 2W
mathend000#. Neste segundo caso, chamado caso limite já é possível determinar um p(t)
mathend000# que verifique a (7-4.34). Porém existe um só sinal possível que é
P(f )= 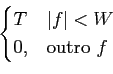 |
(7-4.35) |
cuja forma temporal se escreve
p(t) = 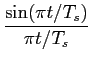 . . |
(7-4.36) |
Isto significa que o menor valor do intervalo de símbolo para o qual é possível ter ISI igual a zero é Ts = 1/2W
mathend000# onde W
mathend000# é a banda do canal de transmissão. Para este valor de Ts
mathend000# e para que a ISI seja zero, a resposta impulsiva combinada do conjunto filtro emissor, canal, receptor deverá ser igual a uma função sinc dada por (7-4.36). Ora neste caso limite é difícil implementar p(t)
mathend000# dado que é uma função não causal ( 0
mathend000# para t < 0
mathend000#) e portanto não realizável. Um atraso de t0
mathend000# em p(t)
mathend000# pode torná-la causal mas impõe sempre uma limitação na forma da sinc, o que acaba por introduzir ISI. Este valor de Ts
mathend000# não é portanto uma solução na prática apesar de corresponder à mais alta taxa de transmissão que pode ser obtida (mínimo valor de Ts
mathend000#).
0
mathend000# para t < 0
mathend000#) e portanto não realizável. Um atraso de t0
mathend000# em p(t)
mathend000# pode torná-la causal mas impõe sempre uma limitação na forma da sinc, o que acaba por introduzir ISI. Este valor de Ts
mathend000# não é portanto uma solução na prática apesar de corresponder à mais alta taxa de transmissão que pode ser obtida (mínimo valor de Ts
mathend000#).
- 3)
- Ts > 1/2W
mathend000# ou seja 1/Ts < 2W
mathend000#. Neste último caso os espectros do sinal p(t)
mathend000# sobrepoem-se e existe assim uma infinidade de possibilidades para a escolha de p(t)
mathend000# que verificam a equação (7-4.34). Devido às razões de realização prática já apontadas anteriormente, as formas de pulso mais utilizadas, e que verificam o critério de Nyquist de ISI igual a zero, pertencem à família dos cosenos elevados (raised cosine) e são dadas por
que tem como transformada de Fourier
P(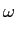 ) = ) = 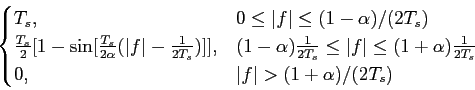 |
(7-4.38) |
onde 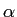 mathend000# é o factor de rolloff tal que
0
mathend000# é o factor de rolloff tal que
0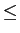
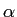
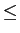 1
mathend000#. Para
1
mathend000#. Para 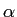 = 0
mathend000#, a função coseno elevado toma a forma de uma função porta no domínio da frequência, por isso corresponde ao caso óptimo do excesso de banda mínimo. Um aumento progressivo de
= 0
mathend000#, a função coseno elevado toma a forma de uma função porta no domínio da frequência, por isso corresponde ao caso óptimo do excesso de banda mínimo. Um aumento progressivo de 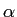 mathend000# tem como efeito um aumento correspondente da largura de banda com uma passagem cada vez mais gradual do valor máximo para zero conforme representado na figura 7.5. O coeficiente
mathend000# tem como efeito um aumento correspondente da largura de banda com uma passagem cada vez mais gradual do valor máximo para zero conforme representado na figura 7.5. O coeficiente 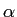 mathend000# variando entre 0 e 1 faz com que o excesso de banda varie entre 0 e 100%.
mathend000# variando entre 0 e 1 faz com que o excesso de banda varie entre 0 e 100%.
Figura 7.5:
função coseno elevado (raised cosine) (a) no tempo e (b) na frequência, para diferentes valores do factor de 'rool-off': 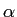 mathend000#=0 (-),
mathend000#=0 (-),
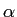 = 0.5
mathend000# (...),
= 0.5
mathend000# (...),
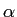 = 0.75
mathend000# (- .) e
= 0.75
mathend000# (- .) e 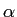 = 1
mathend000# (- -).
= 1
mathend000# (- -).
|
|
Aparentemente a escolha judiciosa da forma do sinal p(t)
mathend000# permite obter uma condição ideal com ISI nula. Porém não devemos esquecer que
p(t) = g(t) * f (t) * b(t)
mathend000# e, na prática, mesmo se g(t)
mathend000# e f (t)
mathend000# podem ser determinados arbitráriamente pelo utilizador, o mesmo não acontece com b(t)
mathend000# que é a resposta impulsiva do canal de transmissão sobre o qual o utilizador tem pouco, ou mesmo nenhum, controlo. O que quer dizer que não existe uma forma fechada para f (t)
mathend000# e g(t)
mathend000# de forma a que p(t)
mathend000# tenha a forma desejada. Mesmo quando b(t)
mathend000# é conhecido, obter uma ISI nula pode ser extremamente dispendioso em termos de complexidade dos filtros g(t)
mathend000# e/ou f (t)
mathend000#.
Diagrama de olho
Uma das formas tradicionais de determinar qualitativamente o grau de ISI de um sistema de comunicação é através do chamado diagrama de olho. O nome vem do facto de que a sua forma é semelhante à do olho humano. Esta é a forma tradicional de teste do grau de ISI porque pode ser facilmente implementada através da observação num osciloscópio do sinal de saída do filtro de recepção no qual a entrada de trigger é o sinal de sincronismo dos símbolos.
Figura 7.6:
um sinal PAM binário com impulsos do tipo coseno elevado e excesso de banda 50% (topo), zoom de uma transição (a) e diagrama de olho(b).
|
|
A figura 7.6 mostra um exemplo de uma sequência de símbolos (topo) e um zoom de uma transição (a) e uma sobreposição de símbolos como poderia ser observada no écran de um osciloscópio (b). Quando existe ISI e o critério de Nyquist não é verificado, o símbolo 0 e 1 tendem a confundir-se fechando o centro do 'olho' verticalmente. O facto do olho estar aberto verticalmente significa igualmente que a quantidade de ruído necessário para produzir erros de identificação é maior e dessa forma compreendemos que quanto maior a abertura vertical maior a imunidade ao ruído. Por outro lado o ponto de cruzamento dos diferentes traços determina a abertura horizontal do olho e depende directamente do sincronismo temporal da taxa de símbolo. No seu geral a forma do olho depende da forma de pulso e do excesso de banda utilizado no coseno elevado. Por exemplo a figura 7.7 mostra dois diagramas de olho, em (a) com 25% de excesso de banda e em (b) com 100% de excesso de banda. Assim podemos ver o benefício de aumentar o excesso de banda obtendo um 'olho' mais aberto e portanto uma maior imunidade ao ruído e uma diminuição dos erros de sincronismo. O preço a pagar foi uma maior largura de banda e no limite uma menor taxa de transmissão na mesma banda e portanto uma diminuição da eficiência espectral do sistema.
Figura 7.7:
diagrama de olho com 25% de excesso de banda (a) e com 100% de excesso de banda (b).
|
|
Como foi referido anteriormente, uma das tarefas mais importantes do emissor é assegurar-se de que cada símbolo do alfabeto se encontra representado por um e só um sinal a transmitir - esta é a etapa de sinalização. Há obviamente um grande número de possibilidades na escolha do conjunto de sinais a utilizar. Neste subcapítulo vamos detalhar e caracterizar algumas delas. Antes disso vamos apenas definir o sinal s(t)
mathend000# em banda base como sendo dado por
| s(t) |
= |
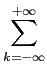 Akg(t - kT), Akg(t - kT), |
|
| |
= |
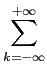 sk(t), sk(t), |
(7-5.01) |
onde T
mathend000# é o intervalo de símbolo.
Modulação por amplitude de impulsos
Amplitude Shift Keying - ASK
Nesta técnica de modulação uma série de impulsos de base são modulados por uma sequência de símbolos de amplitude variável e que constituem ``uma imagem'' da mensagem a transmitir. Os sinais da família de impulsos são dados por
sm(t) = Amg(t), m = 1,..., M, 0 t t T T |
(7-5.02) |
onde
{Am;m = 1,..., M}
mathend000# são os valores possíveis que a sequência de símbolos/bits a transmitir pode tomar, e que modula a amplitude de cada um dos sinais sm(t)
mathend000#. As amplitudes Am
mathend000# encontram-se distribuidas no intervalo
[(1 - M)d,(M - 1)d]
mathend000# sendo que cada nível será dado por
| Am = (2m - 1 - M)d, m = 1,..., M |
(7-5.03) |
e portanto a diferença entre dois níveis sucessivos é de 2d
mathend000#. Dado que a informação se encontra na amplitude dos impulsos, este tipo de modulação é chamado Amplitude Shift Keying - ASK. O sinal g(t)
mathend000# é a ``forma de pulso'' ou pulse shape da qual já falamos anteriormente. Se a taxa de envio de bits à entrada do modulador, também chamada bit rate, de Rb
mathend000# bits por segundo, o intervalo entre dois bits será de Tb = 1/Rb
mathend000#. À saída do modulador teremos uma taxa de símbolo (symbol rate) de Rb/k
mathend000# símbolos por segundo, e portanto o intervalo entre cada símbolo será
Ts = k/Rb = kTb
mathend000#. Comecemos por definir a energia contida em cada uma das funções de base
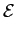 m m |
= |
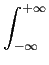 |sm(t) |sm(t) dt, dt, |
|
| |
= |
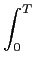 Am2g2(t)dt, Am2g2(t)dt, |
|
| |
= |
A2m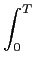 g2(t)dt, g2(t)dt, |
|
| |
= |
A2m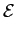 g, g, |
(7-5.04) |
onde
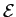 g
mathend000# é a energia do sinal g(t)
mathend000#6. Para simplificar os cálculos que seguem é conveniente exprimir os impulsos de base como
g
mathend000# é a energia do sinal g(t)
mathend000#6. Para simplificar os cálculos que seguem é conveniente exprimir os impulsos de base como
| sm(t) = smf (t), |
(7-5.05) |
onde f (t)
mathend000# é uma função normalizada em energia (energia de f (t)
mathend000# = 1) tal que
f (t) = 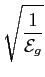 g(t), g(t), |
(7-5.06) |
e assim temos que a amplitude
sm = Am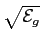 mathend000# (multiplicou-se e dividiu-se por
mathend000# (multiplicou-se e dividiu-se por
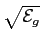 mathend000#). Claramente a possibilidade de confundir o nível m
mathend000# com o nível n
mathend000# depende da distância entre sm(t)
mathend000# e sn(t)
mathend000#. Dado que cada um dos impulsos só difere pela sua amplitude a distância euclidiana mede-se ao longo da recta, o que nos permite escrever
mathend000#). Claramente a possibilidade de confundir o nível m
mathend000# com o nível n
mathend000# depende da distância entre sm(t)
mathend000# e sn(t)
mathend000#. Dado que cada um dos impulsos só difere pela sua amplitude a distância euclidiana mede-se ao longo da recta, o que nos permite escrever
| dmn |
= |
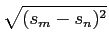 |
|
| |
= |
|Am - An|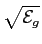 . . |
(7-5.07) |
Visto que dois níveis sucessivos se encontram separados por 2d
mathend000#, a distância mínima entre os sinais correspondentes é
dmin = 2d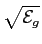 . . |
(7-5.08) |
Modulação por fase de impulsos
(Phase Shift Keying - PSK)
Neste caso e, como o seu nome indica, será a fase e não a amplitude do impulso que variará de acordo com a sequência digital a transmitir. Assim o impulso em banda base escreve-se
| sm(t) |
= |
g(t)ej2 (m-1)/M, (m-1)/M, |
|
| |
= |
g(t)cos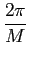 (m - 1) + jg(t)sin (m - 1) + jg(t)sin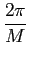 (m - 1). (m - 1). |
(7-5.09) |
Assim, a fase 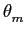 mathend000# da portadora pode tomar os M
mathend000# valores,
{
mathend000# da portadora pode tomar os M
mathend000# valores,
{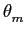 = 2
= 2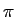 (m - 1)/M;m = 1,..., M}
mathend000#. Podemos notar, fazendo um cálculo análogo ao efectuado no caso da ASK, que cada um dos impulsos utilizados em PSK têm agora uma energia constante
(m - 1)/M;m = 1,..., M}
mathend000#. Podemos notar, fazendo um cálculo análogo ao efectuado no caso da ASK, que cada um dos impulsos utilizados em PSK têm agora uma energia constante
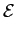 m m |
= |
 |sm(t) |sm(t) dt, dt, |
|
| |
= |
 g2(t), g2(t), |
|
| |
= |
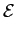 g. g. |
(7-5.10) |
Utilizando (7-5.9) podemos notar que cada função de base pode ser representada como uma combinação linear de duas funções ortogonais f1(t)
mathend000# e f2(t)
mathend000#, tais que
| sm(t) = sm1f1(t) + sm2f2(t), |
(7-5.11) |
onde
| f1(t) |
= |
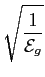 g(t), g(t), |
(7-5.12) |
| f2(t) |
= |
j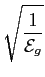 g(t), g(t), |
(7-5.13) |
e finalmente, tomando como vectores unitários as funções f1(t)
mathend000# e f2(t)
mathend000# podemos representar o sinal sm(t)
mathend000# como um vector 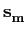 mathend000# de coordenadas
mathend000# de coordenadas
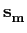 |
= |
 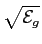 cos cos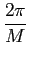 (m - 1), (m - 1),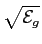 sin sin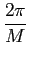 (m - 1) (m - 1)![$\displaystyle \left.\vphantom{\sqrt{\mathcal{E}_g} \cos {{2\pi}\over M}(m-1) , \sqrt{\mathcal{E}_g} \sin {{2\pi}\over M}(m-1)}\right]$](img432.png) |
|
| |
= |
[sm1, sm2], |
(7-5.14) |
Torna-se assim fácil compreender a representação dos impulsos de base num referencial ortonormado de acordo com a figura 7.8 para M=2, 4 e 8. Note-se que os símbolos atribuidos a cada ponto do espaço encontram-se distribuidos de tal forma a só mudar um bit entre pontos contíguos, com a intenção de minimizar o erro cometido (código de Gray - Gray coding).
Figura 7.8:
diagrama de espaço de sinais para a modulação PSK.
|
|
Da mesma forma que com ASK, em PSK, o erro entre dois níveis sucessivos depende da distância euclidiana entre dois pontos no plano, dada por
| dmn |
= |
|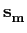 - - 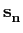 | | |
|
| |
= |
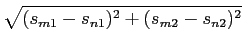 , , |
|
| |
= |
![$\displaystyle \sqrt{{\mathcal{E}_g\left[\cos[{{2\pi}\over M}(m-1)]-\cos[{{2\pi}...
...hcal{E}_g\left[\sin[{{2\pi}\over M}(m-1)]-\sin[{{2\pi}\over M}(n-1)]\right]^2}}$](img436.png) |
|
| |
= |
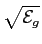 ![$\displaystyle \sqrt{{2-2\cos[{{2\pi}\over M}(m-1)]\cos[{{2\pi}\over M}(n-1)]-2\sin[{{2\pi}\over M}(m-1)]\sin[{{2\pi}\over M}(m-1)]}}$](img437.png) |
|
| |
= |
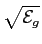 ![$\displaystyle \sqrt{{2-2\cos \left[{{2\pi}\over M}(m-n)\right]}}$](img438.png) , , |
(7-5.15) |
onde o seu valor mínimo é obtido para m = n + 1
mathend000# de onde
dmin = 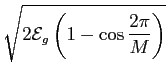 . . |
(7-5.16) |
Modulação de amplitude em quadratura
(Quadrature Amplitude Modulation - QAM)
A modulação de amplitude em quadratura (QAM) permite obter a mesma eficiência da modulação ASK-SSB utilizando dois bits de informação em duas portadoras em quadratura (90 graus) uma da outra. É um pouco como se fosse ASK em PSK com M = 2
mathend000#. Neste caso os sinais de base escrevem-se
| sm(t) |
= |
(Amc + jAms)g(t), m = 1,..., M, 0 t t T, T, |
|
| |
= |
Amcg(t) - jAmsg(t). |
(7-5.17) |
Deste modo cada impulso leva o dobro da informação através da codificação de Amc
mathend000# e Ams
mathend000#, amplitudes das componentes em fase e em quadratura da portadora, respectivamente. Outra forma de ver a relação entre QAM, ASK e PSK é de escrever o sinal da equação (7-5.17) como
| sm(t) |
= |
Vmg(t)ej , , |
|
| |
= |
Vmg(t)cos + jVmg(t)sin + jVmg(t)sin , , |
(7-5.18) |
onde
Vm = 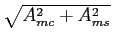 mathend000# e
mathend000# e
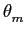 = arctan(Ams/Amc)
mathend000#, o que demonstra que QAM pode ser visto como uma combinação de modulação de amplitude e modulação de fase. Como no caso PSK, também em QAM os sinais de base sm(t)
mathend000# podem ser representados em forma vectorial a partir de um conjunto das funções de base (7-5.13) com as coordenadas
= arctan(Ams/Amc)
mathend000#, o que demonstra que QAM pode ser visto como uma combinação de modulação de amplitude e modulação de fase. Como no caso PSK, também em QAM os sinais de base sm(t)
mathend000# podem ser representados em forma vectorial a partir de um conjunto das funções de base (7-5.13) com as coordenadas
onde, como habitualmente
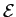 g
mathend000# é a energia do ``pulso'' de base g(t)
mathend000#. A distância euclidiana entre dois pontos m
mathend000#, n
mathend000# é neste caso dada por
g
mathend000# é a energia do ``pulso'' de base g(t)
mathend000#. A distância euclidiana entre dois pontos m
mathend000#, n
mathend000# é neste caso dada por
| dmn |
= |
|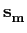 - - 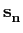 |, |, |
|
| |
= |
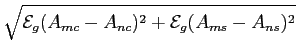 , , |
(7-5.20) |
Figura 7.9:
constelação QAM para o caso cartesiano equidistante e para M=16.
|
|
A distância mínima entre dois pontos contíguos no espaço de sinais QAM depende da forma da disposição da grelha de pontos. No caso em que as amplitudes discretas variam de acordo com
{(2m - 1 - M)d;m = 1,..., M}
mathend000# a grelha toma uma forma rectangular como a representada na figura 7.9 para o caso M = 16
mathend000# e, nesse caso, a distância mínima é dada por
dmin = 2d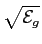 . . |
(7-5.21) |
Podemos agora generalizar a ideia introduzida com QAM a ordens superiores de ASK e PSK, combinando sempre os dois tipos de modulação. Assim, se notarmos M1
mathend000# o número de níveis de ASK, e M2
mathend000# o número de níveis de PSK, temos que o número de níveis total obtido pela combinação ASK-PSK, é M = M1M2
mathend000#. Isto significa que se podem representar k = m1 + m2
mathend000# símbolos onde
M1 = 2m1
mathend000# e
M2 = 2m2
mathend000#. A taxa de transmissão de símbolos encontra-se então reduzida a
1/Ts = R/(m1 + m2)
mathend000#. A título de exemplo, a figura 7.10 representa os diagramas de espaço de sinais para a modulação combinada ASK-PSK, para M = 8
mathend000# e M = 16
mathend000#.
Figura 7.10:
diagrama de espaço de sinais para a modulação ASK-PSK, M=8 e M=16.
|
|
Modulação de impulsos em frequência
(Frequency Shift Keying - FSK)
Ficou claro da secção anterior que a modulação em amplitude e fase permite representar o alfabeto de sinais num espaço bidimensional. Generalizando esta ideia podemos representar sinais em espaços multidimensionais utilizando o domínio temporal, ou frequencial ou os dois. Assim, particionando um determinado intervalo de tempo (ou de frequência) em, por exemplo, N
mathend000# sub-intervalos, em cada um pode ser utilizada uma modulação de impulsos binária (PM) seja de amplitude ou de fase. Obtêm-se assim N
mathend000# sinais por subdivisão do intervalo temporal em N
mathend000# intervalos de duração T' = T/N
mathend000# ou subdivisão da banda de frequência em intervalos de banda
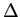 f = W/N
mathend000#.
f = W/N
mathend000#.
A título de exemplo de transmissão por modulação multidimensional consideraremos aqui o caso da modulação de impulsos em frequência FSK (frequency shift keying), na qual a separação entre níveis se faz através de variações em frequência. Assim, a família de sinais em banda base escreve-se
| sm(t) |
= |
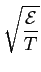 ej2 ej2 m m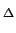 ft, m = 1,..., M, 0 ft, m = 1,..., M, 0 t t T, T, |
|
| |
= |
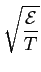 cos(2 cos(2 m m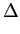 ft) + j ft) + j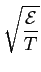 sin(2 sin(2 m m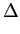 ft), ft), |
(7-5.22) |
onde
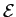 mathend000# é um coeficiente de normalização correspondente à energia num símbolo/bit. Para o caso em que
mathend000# é um coeficiente de normalização correspondente à energia num símbolo/bit. Para o caso em que
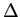 f = 1/2T
mathend000# os M
mathend000# sinais FSK escrevem-se
f = 1/2T
mathend000# os M
mathend000# sinais FSK escrevem-se
sm(t) = 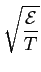 cos( cos( mt/T) + j mt/T) + j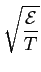 sin( sin( mt/T) m = 1,..., M, 0 mt/T) m = 1,..., M, 0 t t T, T, |
(7-5.23) |
e podem ser representados como outros tantos vectores de dimensão M
mathend000#, dados por
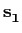 |
= |
[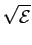 , 0, 0,..., 0] , 0, 0,..., 0] |
|
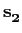 |
= |
[0,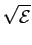 , 0,..., 0] , 0,..., 0] |
|
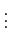 |
= |
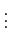 |
|
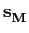 |
= |
[0, 0, 0,..., 0,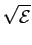 ], ], |
(7-5.24) |
onde cada sinal tem por coordenada apenas
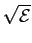 mathend000# na direção m
mathend000# e zero em todas as outras M - 1
mathend000# direções. Este tipo de representação tem mais duas propriedades interessantes que convem realçar: a primeira é de que se trata de uma modulação não-coerente no sentido em que o ``slicer'' no receptor não tem de ser síncrono com o emissor, mas apenas tem de amostrar o sinal q(t)
mathend000# à taxa de símbolo/bit Ts
mathend000#; a segunda é que se pode demonstrar que para
mathend000# na direção m
mathend000# e zero em todas as outras M - 1
mathend000# direções. Este tipo de representação tem mais duas propriedades interessantes que convem realçar: a primeira é de que se trata de uma modulação não-coerente no sentido em que o ``slicer'' no receptor não tem de ser síncrono com o emissor, mas apenas tem de amostrar o sinal q(t)
mathend000# à taxa de símbolo/bit Ts
mathend000#; a segunda é que se pode demonstrar que para
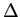 f = 1/2T
mathend000# os sinais sm(t)
mathend000# modulados em FSK são ortogonais entre si. Veremos mais tarde que esta segunda propriedade é de grande importância quando da detecção do sinal no receptor. Com efeito se calcularmos o coeficiente de correlação (função de correlação para o ponto ``zero lag'') entre dois sinais m
mathend000# e n
mathend000# temos
f = 1/2T
mathend000# os sinais sm(t)
mathend000# modulados em FSK são ortogonais entre si. Veremos mais tarde que esta segunda propriedade é de grande importância quando da detecção do sinal no receptor. Com efeito se calcularmos o coeficiente de correlação (função de correlação para o ponto ``zero lag'') entre dois sinais m
mathend000# e n
mathend000# temos
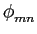 |
= |
Re 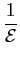 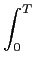 sm(t)sn * (t)dt sm(t)sn * (t)dt![$\displaystyle \left.\vphantom{{1\over \mathcal{E}} \int_0^T s_m(t) s_n^{\ast}(t) dt}\right]$](img456.png) |
|
| |
= |
Re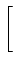 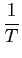 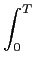 ej2 ej2 m m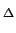 fte-j2 fte-j2 n n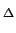 ftdt ftdt![$\displaystyle \left.\vphantom{{1\over T} \int_0^T e^{j2\pi m\Delta ft} e^{-j2\pi n\Delta ft} dt}\right]$](img458.png) |
|
| |
= |
Re![$\displaystyle \left(\vphantom{{1\over T} \left[{{e^{j2\pi (m-n)\Delta ft}}\over {j2\pi (m-n)\Delta f}}\right]_0^T }\right.$](img459.png) 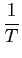  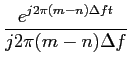 ![$\displaystyle \left.\vphantom{{{e^{j2\pi (m-n)\Delta ft}}\over {j2\pi (m-n)\Delta f}}}\right]_{0}^{T}$](img462.png) ![$\displaystyle \left.\vphantom{{1\over T} \left[{{e^{j2\pi (m-n)\Delta ft}}\over {j2\pi (m-n)\Delta f}}\right]_0^T }\right)$](img463.png) |
|
| |
= |
Re![$\displaystyle \left[\vphantom{e^{j\pi (m-n)\Delta fT} {{\sin[\pi \Delta f (m-n)T]}\over {\pi \Delta f (m-n)T}}}\right.$](img464.png) ej ej (m-n) (m-n) fT fT![$\displaystyle {{\sin[\pi \Delta f (m-n)T]}\over {\pi \Delta f (m-n)T}}$](img465.png) ![$\displaystyle \left.\vphantom{e^{j\pi (m-n)\Delta fT} {{\sin[\pi \Delta f (m-n)T]}\over {\pi \Delta f (m-n)T}}}\right]$](img466.png) |
|
| |
= |
![$\displaystyle {{\sin[\pi \Delta f (m-n)T]}\over {\pi \Delta f (m-n)T}}$](img465.png) cos( cos(  f (m - n)T) f (m - n)T) |
|
e finalmente
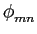 = = ![$\displaystyle {{\sin[2\pi \Delta f (m-n)T]}\over {2\pi \Delta f (m-n)T}}$](img467.png) , , |
(7-5.25) |
que é um ``familiar'' seno de x
mathend000# sobre x
mathend000#, cujos zeros são obtidos quando se anula o numerador, i.e., para
2
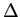 f (m - n)T = k
f (m - n)T = k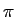 mathend000# ou ainda quando
mathend000# ou ainda quando
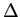 f = k/[(m - n)2T]
mathend000# o que indica que, para m
f = k/[(m - n)2T]
mathend000# o que indica que, para m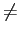 n
mathend000#,
n
mathend000#,
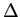 f = 1/2T
mathend000# corresponde à separação mínima entre frequências para que os M
mathend000# sinais emitidos às M
mathend000# frequências sejam ortogonais. A distância no espaço de sinais pode ser calculada directamente a partir de (7-5.24) e é dada por
f = 1/2T
mathend000# corresponde à separação mínima entre frequências para que os M
mathend000# sinais emitidos às M
mathend000# frequências sejam ortogonais. A distância no espaço de sinais pode ser calculada directamente a partir de (7-5.24) e é dada por
dmn = 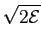 , , |
(7-5.26) |
e que sendo independente de m
mathend000# e n
mathend000# é também a distância mínima.
Modulação de impulsos em banda passante
Na prática a maioria dos canais de transmissão não são compatíveis com a transmissão de um sinal em banda base e por isso é necessário modular o sinal em banda passante. Quem diz modulação diz também desmodulação do mesmo sinal ao nível do receptor. O princípio, geralmente verificado na prática, é que o processo de modulação e desmodulação deverá ser transparente para o utilizador tanto do ponto de vista do tratamento matemático como do desempenho do sistema.
Como já tivemos ocasião de ver a passagem de um sinal complexo s(t)
mathend000# em banda base para um sinal x(t)
mathend000# em banda passante traduz-se por
x(t) = Re{s(t)ej2 fct}, fct}, |
(7-6.01) |
onde, se s(t)
mathend000# for em banda base, x(t)
mathend000# será em banda passante. Anteriormente discutimos vários métodos de modulação / sinalização, entre os quais ASK, PSK, FSK e QAM. Tomaremos aqui o caso mais eficiente que é a modulação QAM. A grande vantagem deste tipo de modulação é de que permite a transmissão de sinais em banda base complexos onde a parte real e a parte imaginária podem não ter forçosamente nenhuma ligação entre si, i.e., ambas podem conter informação. Na prática, isto significa que se
s(t) = 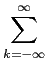 Akg(t - kT), Akg(t - kT), |
(7-6.02) |
os coeficientes Ak
mathend000# ou a ``função de pulso'' g(t)
mathend000#, ou ambos, podem ser complexos. Em particular, quase nunca acontece que g(t)
mathend000# seja complexo, porém, a possibilidade que Ak
mathend000# tome valores complexos é altamente interessante porque duplica a quantidade de informação que pode ser contida no mesmo alfabeto. O esquema blocos de um tal modulador (transmissor) encontra-se representado na figura 7.11.
![]() (k - m)
(k - m)
![]()
![]()
![]()
![]() }
}
![]() |
|
![]() |
|
![]() |/Ts
|/Ts
![]() =
= 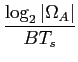 ,
,![]() = E[|A
= E[|A![]() ]
]
![]() (
(![]() )
)
![]()
![]() (t +
(t + ![]() , t) =
, t) = ![]() (t + Ts +
(t + Ts + ![]() , t + Ts),
, t + Ts),![]() , +
, + ![]() ]
]
![]() (t +
(t + ![]() , t)
, t)
![]()
![]() g(t - nTs)
g(t - nTs)![]() ] -
] - ![]() ,
,![]() [
[
![]() (
(![]() )
)
![]() (i)
(i)
![]() (i)
(i)
![]()
![]()
![]() (i) = E[Am+iAm * ]
(i) = E[Am+iAm * ]
![]() m em relevo dois tipos de componentes espectrais: 1) o primeiro termo é um espectro contínuo e depende unicamente do espectro da ``forma do pulso'' g(t)
m em relevo dois tipos de componentes espectrais: 1) o primeiro termo é um espectro contínuo e depende unicamente do espectro da ``forma do pulso'' g(t)
![]() = 0
= 0
![]()
![\includegraphics[width=7cm]{figs/square_pulse.eps}](img375.png)
![\includegraphics[width=7cm]{figs/spec_square_pulse.eps}](img376.png)
![\begin{displaymath}\begin{cases}
0 & t \in [-\infty,0[ \\ A & t \in [0,T] \\ 0 & t \in ]T,\infty[ \end{cases}\end{displaymath}](img377.png)
![]()
![]() Ae-j2
Ae-j2![]() ftdt,
ftdt,![]()
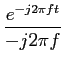
![]()
![]()
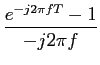
![]()
![]() fT
fT![]()
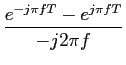
![]()
![]() fT
fT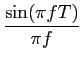 ,
,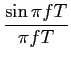 e-j
e-j![]() fT,
fT,![]() = (AT)2
= (AT)2![]()
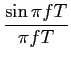
![]() ,
,![]()
![\includegraphics[width=7cm]{figs/rc_pulse.eps}](img392.png)
![\includegraphics[width=7cm]{figs/spec_rc_pulse.eps}](img393.png)
![\begin{displaymath}\begin{cases}
{A\over 2}\left[ 1 + \cos {{2\pi}\over T}(t-{T\...
...2})\right], & 0 \le t \le T \\ 0 & t \not\in [0,T], \end{cases}\end{displaymath}](img394.png)
![]()
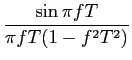 e-j
e-j![]() fT,
fT,![]() =
= ![]()
![]()
![]()
![]()
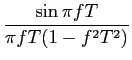
![]() ,
,![]() /W
/W
![]() /W
/W
![]() /Ts
/Ts
![]() /Ts
/Ts
![]() )
)
![]() ) = 0
) = 0
![]() |> W
|> W
![\includegraphics[width=12cm]{figs/zero-forcing.eps}](img409.png)
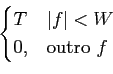
![]() 0
0
![]()
![]()
![]()
![]() 1
1
![]() = 0
= 0
![]()
![]()
![]()
![]() = 0.5
= 0.5
![]() = 0.75
= 0.75
![]() = 1
= 1
![\includegraphics[width=15cm]{figs/fig6-2.eps}](img419.png)
![\includegraphics[width=15cm]{figs/fig6-3.eps}](img420.png)
![]() g
g
![]()
![]()
![]()
![]() = 2
= 2![]() (m - 1)/M;m = 1,..., M}
(m - 1)/M;m = 1,..., M}
![]()
![]()
![]() = arctan(Ams/Amc)
= arctan(Ams/Amc)
![]() g
g
![]() f = W/N
f = W/N
![]()
![]() f = 1/2T
f = 1/2T
![]()
![]() f = 1/2T
f = 1/2T
![]()
![]()
![]()
![]() sm(t)sn * (t)dt
sm(t)sn * (t)dt![]()
![]()
![]()
![]() ej2
ej2![]() m
m![]() fte-j2
fte-j2![]() n
n![]() ftdt
ftdt![]()
![]()
![]()
![]()
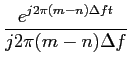
![]()
![]()
![]() ej
ej![]() (m-n)
(m-n)![]() fT
fT![$\displaystyle {{\sin[\pi \Delta f (m-n)T]}\over {\pi \Delta f (m-n)T}}$](img465.png)
![]()
![$\displaystyle {{\sin[\pi \Delta f (m-n)T]}\over {\pi \Delta f (m-n)T}}$](img465.png) cos(
cos(![]()
![]() f (m - n)T)
f (m - n)T)![]() =
= ![$\displaystyle {{\sin[2\pi \Delta f (m-n)T]}\over {2\pi \Delta f (m-n)T}}$](img467.png) ,
,![]()
![]() f (m - n)T = k
f (m - n)T = k![]()
![]() f = k/[(m - n)2T]
f = k/[(m - n)2T]
![]() n
n
![]() f = 1/2T
f = 1/2T
![]() ,
,![\includegraphics[width=15cm]{figs/fig6-1.eps}](img340.png)
 Amg(t - mTs),
Amg(t - mTs), Amp(t - mTs) + u(t),
Amp(t - mTs) + u(t),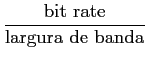 ,
,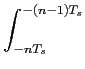 g(u +
g(u + 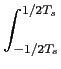 PA(f )ej2
PA(f )ej2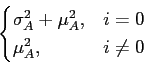
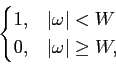
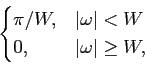
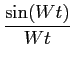 .
.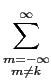 Amp(kTs - mTs) + u(kTs),
Amp(kTs - mTs) + u(kTs),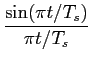 .
.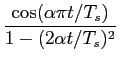
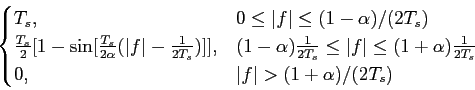
![\includegraphics[width=15cm]{figs/fig6-4.eps}](img421.png)
![\includegraphics[width=15cm]{figs/sinais-PSK.eps}](img433.png)
![$\displaystyle \sqrt{{\mathcal{E}_g\left[\cos[{{2\pi}\over M}(m-1)]-\cos[{{2\pi}...
...hcal{E}_g\left[\sin[{{2\pi}\over M}(m-1)]-\sin[{{2\pi}\over M}(n-1)]\right]^2}}$](img436.png)
![$\displaystyle \sqrt{{2-2\cos[{{2\pi}\over M}(m-1)]\cos[{{2\pi}\over M}(n-1)]-2\sin[{{2\pi}\over M}(m-1)]\sin[{{2\pi}\over M}(m-1)]}}$](img437.png)
![$\displaystyle \sqrt{{2-2\cos \left[{{2\pi}\over M}(m-n)\right]}}$](img438.png) ,
,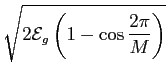 .
.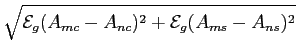 ,
,![\includegraphics[width=6cm]{figs/constellation-qam.eps}](img444.png)
![\includegraphics[width=15cm]{figs/QAM816.eps}](img445.png)