Subsections
Modulação analógica de onda sinusoidal
A modulação de portadora sinusoidal compreende a modulação de amplitude, de fase e de frequência, que constituem uma família de métodos de modulação nos quais a amplitude, a fase ou a frequência de uma sinusoide de frequência central pré-determinada é alterada em função do sinal modulador. A modulação de amplitude (AM) é caracterizada por uma relativa simplicidade de representação e uma fraca necessidade de banda passante. Por outro lado a sua eficiência em termos de potência é bastante baixa quando comparada com os métodos de modulação angular (fase e frequência). Os métodos de modulação AM são ainda hoje frequentemente empregues em difusão rádio e TV, comunicações ponto a ponto (SSB) e multiplexagem em telefonia. Os métodos de modulação de fase e frequência são mais difíceis de implementar mas bastante mais eficientes e imunes ao ruído e daí
mathend000# uma qualidade de recepção bastante superior.
Uma portadora de frequência central fc
mathend000# e amplitude Ac
mathend000# é modulada em amplitude por um sinal m(t)
mathend000# quando se escreve
s(t) = [1 + a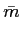 (t)]c(t), (t)]c(t), |
(5-1.01) |
onde m(t)
mathend000# é a mensagem a transmitir, passa-baixo, dentro da banda - W, W
mathend000# e
c(t) = Accos(2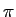 fct)
mathend000# é a portadora onde se supõe que fc > W
mathend000# e
0
fct)
mathend000# é a portadora onde se supõe que fc > W
mathend000# e
0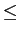 a
a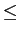 1
mathend000# é um coeficiente real denominado indice de modulação. O sinal
1
mathend000# é um coeficiente real denominado indice de modulação. O sinal 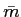 (t)
mathend000# é a mensagem m(t)
mathend000# normalizada, i.e., tal que
(t)
mathend000# é a mensagem m(t)
mathend000# normalizada, i.e., tal que
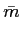 (t) = (t) = 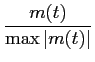 . . |
(5-1.02) |
Obviamente (como aliás já vimos no capítulo 2.1) este tipo de modulação resulta no domínio da frequência num espectro que se escreve
S(f )= 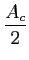 [a [a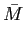 (f - fc) + (f - fc) + 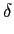 (f - fc) + a (f - fc) + a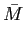 (f + fc) + (f + fc) + 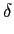 (f + fc)], (f + fc)], |
(5-1.03) |
onde o espectro do sinal modulador (normalizado) foi deslocado de - fc
mathend000# e + fc
mathend000#, frequências às quais encontramos igualmente um impulso correspondente à portadora. Todo o espectro foi multiplicado por 1/2
mathend000# devido ao princípio de conservação de energia. A banda ocupada pelo sinal modulador é de 2W
mathend000#.
Exemplo: considere o sinal
m(t) = 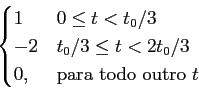 |
(5-1.04) |
com t0 = 0.15
mathend000# e que modula uma portadora de frequência fc = 250
mathend000# Hz, com Ac = 2
mathend000# e um índice de modulação a = 0.8
mathend000#.
- a)
- determine a expressão do sinal modulador normalizado
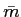 (t)
mathend000#
(t)
mathend000#
- b)
- calcule a expressão do sinal modulado s(t)
mathend000#
- c)
- determine o espectro de
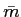 (t)
mathend000# e de s(t)
mathend000#
(t)
mathend000# e de s(t)
mathend000#
O sinal modulador normalizado escreve-se facilmente, tendo em conta que
max|m(t)|= 2
mathend000#
o que implica que
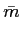
(
t) =
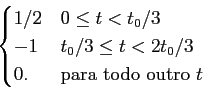
mathend000#
A expressão do sinal modulado obtem-se começando por considerar que o sinal modulador normalizado se escreve como uma soma de duas funções porta de largura t0/3
mathend000#: uma positiva, de amplitude 1/2 e atrasada de t0/6
mathend000#, outra negativa de amplitude -1 e atrasada de t0/2
mathend000#. Assim podemos escrever
mathend000#
onde p(t)
mathend000# é a função porta típica, centrada e de amplitude unidade. Podemos então escrever o sinal modulado
| s(t) |
= 2[1+0.8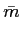 (t)]cos(500 (t)]cos(500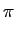 t) t) |
| |
= ![$\displaystyle {2\left[1+0.4 p\left({{t-t_0/6}\over {t_0/3}}\right) -
0.8 p\left({{t-t_0/2}\over {t_0/3}}\right)\right]\cos(500\pi t)}$](img253.png) . . |
mathend000#
O espectro do sinal modulador m(t)
mathend000# obtem-se a partir da expressão temporal acima sabendo que
TF[p(t)] = sinc(f )
mathend000# e portanto que devido a um atraso t0
mathend000# e a uma largura de porta 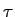 mathend000# temos que
mathend000# temos que
mathend000#
de onde aplicando à expressão de 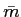 (t)
mathend000# acima obtemos
(t)
mathend000# acima obtemos
mathend000#
Por outro lado a expressão do espectro do sinal modulado obtem-se a partir da equação anterior deslocando-a de + fc
mathend000# e de - fc
mathend000# e adicionando os Diracs às mesmas frequências, correspondentes à portadora e tendo em conta que Ac = 2
mathend000#,
mathend000#
que é o espectro do sinal modulado s(t)
mathend000#.
Podemos calcular igualmente a potência do sinal modulado que se exprime utilizando (2-2.58) como
| Ps |
= |
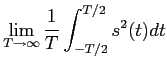 |
(5-1.05) |
| |
= |
![$\displaystyle {\lim_{T \to \infty} {1\over T}\int_{-T/2}^{T/2} A_c^2[1+a\bar m(t)]^2 \cos^2(2\pi ft) dt}$](img264.png) |
(5-1.06) |
| |
= |
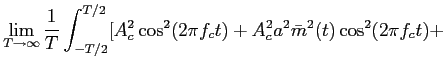 |
(5-1.07) |
| |
|
+2Ac2a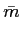 (t)cos(2 (t)cos(2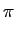 fct)]dt fct)]dt |
(5-1.08) |
| |
= |
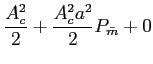 , , |
(5-1.09) |
onde se assumiu que a média do sinal modulador normalizado 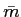 (t)
mathend000# era igual a zero.
(t)
mathend000# era igual a zero.
Exemplo: voltando ao sinal m(t)
mathend000# do exemplo anterior, calcular as potências
P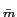 mathend000# e Ps
mathend000#.
mathend000# e Ps
mathend000#.
Podemos por exemplo calcular para o sinal não normalizado m(t)
mathend000#,
| Pm |
= 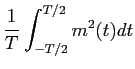 |
| |
= 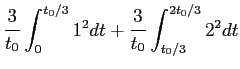 |
| |
= 5, |
mathend000#
de onde podemos deduzir
mathend000#
No que diz respeito à potência do sinal s(t)
mathend000# podemos escrever, utilizando (5-1.9), com Ac = 2
mathend000# e a = 0.8
mathend000#
| Ps |
= 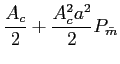 |
| |
= 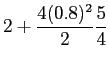 |
| |
= 3.6. |
mathend000#
Neste caso, dito AM-CS (Amplitude Modulation - Carrier Suppressed) temos o mesmo tipo de modulação que no caso anterior, a diferença consistindo apenas na supressão da moduladora. Assim, o sinal modulado escreve-se
| s(t) = m(t)c(t), |
(5-2.01) |
onde, como anteriormente, m(t)
mathend000# é a mensagem ou sinal modulador e c(t)
mathend000# é a portadora. Com
c(t) = Accos(2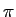 fct)
mathend000# encontra-se facilmente o espectro de s(t)
mathend000# como sendo
fct)
mathend000# encontra-se facilmente o espectro de s(t)
mathend000# como sendo
S(f )= 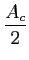 M(f - fc) + M(f - fc) + 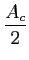 M(f + fc). M(f + fc). |
(5-2.02) |
A principal vantagem deste tipo de modulação é o de a potência necessária no sinal modulado ser bastante inferior mantendo no entanto a mesma quantidade de informação transmitida. É por isso um sistema de modulação mais eficaz que o anterior. A potência em S(f )
mathend000# é
Ps = 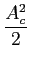 Pm, Pm, |
(5-2.03) |
valor inferior de Ac/2
mathend000# em relação ao caso anterior.
Figura 5.1:
esquema de blocos para modulação de amplitude (AM).
|
|
A realização prática da modulação de amplitude (seja com ou sem portadora) pode ser efectuada através de um circuito de blocos conforme exemplificado na figura 5.1. Este circuito denominado ``modulador multiplicador'', utiliza um multiplicador de alta frequência para efectuar a modulação da portadora gerada num oscilador local pelo sinal útil previamente limitado e amplificado pelo respectivo coeficiente de modulação. Assim o sinal modulado escreve-se
| s(t) |
= |
a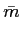 (t)Accos (t)Accos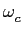 t + Accos t + Accos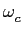 t t |
|
| |
= |
Ac[1 + a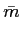 (t)]cos (t)]cos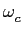 t. t. |
|
A implementação da modulação AM-CS faz-se apenas com o multiplicador omitindo o somador. O problema prático em termos de linearidade e fidelidade na banda vem da necessidade de empregar um multiplicador de alta frequência. Existem várias estratégias para obviar, ou pelo menos atenuar, este problema (ver páginas 158 e seguintes de [11]).
Nos dois exemplos de modulação descritos anteriormente a informação relativa à mensagem m(t)
mathend000# encontrava-se à frequência fc
mathend000# e depois repetida em - fc
mathend000#. Isto é redundante. Na modulação em banda lateral única (SSB - single side band) pretende-se acabar com esta redundância de forma a dividir por dois a potência necessária para transmitir a mesma quantidade de informação. A figura 5.2 mostra um sinal m(t)
mathend000# em banda base (figura 5.2(a)) e o seu espectro modulado em AM-DSB (figura 5.2(b)). Para transmitir a informação contida na figura 5.2(a) bastaria que o sinal modulado contivesse as partes superiores e inferiores do espectro de m(t)
mathend000# resultando da passagem do espectro da figura 5.2(b), por exemplo, por um filtro passa-alto de frequência de corte fc
mathend000# (representado pela linha em ponteado) resultando no espectro indicado na figura 5.2(c). Obviamente um raciocínio idêntico poderia ser feito com uma filtragem passa-baixo de frequência de corte fc
mathend000# e cujo resultado seria o de preservar no sinal modulado apenas a componente inferior da mensagem m(t)
mathend000#. A modulação exemplificada no primeiro caso é chamada USSB - upper SSB e no segundo é LSSB - lower SSB. Como já tivemos ocasião de ver no capítulo 2.2.2, um sinal apenas com a componente espectral positiva escreve-se
Figura 5.2:
exemplificação da modulação AM-SSB.
|
|
m'(t) = 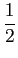 [m(t) + j [m(t) + j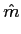 (t)], (t)], |
(5-3.01) |
onde o 1/2 serve para manter uma energia constante e 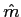 (t)
mathend000# é a transformada de Hilbert de m(t)
mathend000#. Neste caso o sinal modulado no domínio do tempo escreve-se
(t)
mathend000# é a transformada de Hilbert de m(t)
mathend000#. Neste caso o sinal modulado no domínio do tempo escreve-se
s'(t) = Acm'(t)cos(2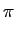 fct). fct). |
(5-3.02) |
O espectro de s'(t)
mathend000# obtem-se sabendo que
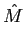 (f )= (f )= 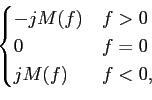 |
(5-3.03) |
e portanto
M'(f )= 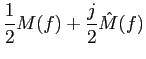 |
(5-3.04) |
e ainda
M'(f )= 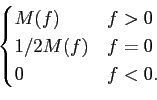 |
(5-3.05) |
A optenção do espectro de s'(t)
mathend000# de (5-3.2) Finalmente,
S'(f )= 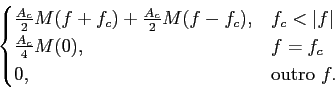 |
(5-3.06) |
No caso agora exemplificado apenas foram retidas as frequências positivas e por isso trata-se do caso USSB. No caso LSSB teríamos
m'(t) = 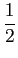 [m(t) - j [m(t) - j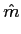 (t)], (t)], |
(5-3.07) |
e como resultado final para o espectro de s'(t)
mathend000#,
S'(f )= 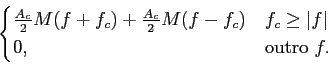 |
(5-3.08) |
A realização prática da modulação SSB é substancialmente mais complicada do que no caso da modulação AM, pois na maior parte das implementações serão necessários dois multiplicadores e pelo menos um filtro passa-banda, para além de outros somadores e osciladores locais. De uma forma muito básica um sinal SSB pode ser gerado pelo circuito conceptual da figura 5.3.
Figura 5.3:
exemplo do circuito conceptual para modulação SSB.
|
|
Nesta figura podemos ver o sinal modulador m(t)
mathend000#, o oscilador local e um circuito modulador DSB tradicional, agora seguido de um filtro passa banda para filtragem seja da banda lateral superior ou inferior do sinal DSB, conforme se trate de modulação USSB ou LSSB, respectivamente. Um circuito completo de modulação SSB encontra-se representado na figura 5.4.
Figura 5.4:
exemplo do circuito de translação de fase para modulação SSB.
|
|
Esta implementação utiliza directamente a equação
s'(t) = 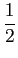 Ac[m(t)cos Ac[m(t)cos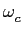 t t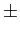 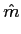 (t)sin (t)sin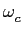 t], t], |
(5-3.09) |
obtida pela substituição de (5-3.1) em (5-3.2) e onde o termo em
sin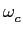 t
mathend000# é obtido através de
cos(
t
mathend000# é obtido através de
cos(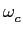 t - 90o)
mathend000#.
t - 90o)
mathend000#.
A modulação vestigial4 vem dar resposta a uma necessidade frequentemente encontrada em transmissão da informação, como por exemplo do sinal de televisão, fax e sinais de alta velocidade, que são sinais com um conteúdo espectral de baixa frequência muito significativo. Enquanto SSB é efectivo em termos de banda passante mas tem uma resposta em baixa frequência de fraca qualidade (termo 1/2M(f )
mathend000# para f = 0
mathend000#), DSB tem uma boa resposta em baixa frequência mas é ineficiente em termos de banda (duas vezes maior do que em SSB). Na modulação VSB o espectro em baixa frequência é previligiado em relação às altas frequências, mantendo no entanto a eficiência da modulação SSB.
VSB é um derivado de DSB, na qual uma das bandas passa quase completamente e da outra apenas passa ``um vestígio'', daí a noção de ``vestigial''. Neste sentido VSB utiliza um filtro de banda lateral, do qual podem existir muitas versões mas cujo o aspecto típico se encontra representado na figura 5.5.
Figura 5.5:
filtro vestigial.
|
|
A expressão do sinal modulado obtem-se a partir de (5-3.2)
s'(t) = Acm'(t)cos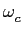 t, t, |
(5-4.01) |
mas agora com
m'(t) = 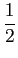 {m(t) - j[ {m(t) - j[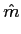 (t) + m (t) + m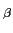 (t)]}, (t)]}, |
(5-4.02) |
onde m(t)
mathend000# é o sinal mensagem modulador, 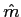 (t)
mathend000# que já foi definido e
m
(t)
mathend000# que já foi definido e
m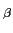 (t)
mathend000# é o sinal mensagem obtido à saída do filtro vestigial
(t)
mathend000# é o sinal mensagem obtido à saída do filtro vestigial
m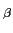 (t) = 2j (t) = 2j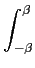 H H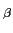 (f )M(f )ej2 (f )M(f )ej2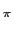 ftdf, ftdf, |
(5-4.03) |
onde
H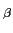 (f )
mathend000# é o filtro vestigial tendo, a título de exemplo, a resposta em frequência da figura 5.5. Substituindo (5-4.3) em (5-4.2) obtemos
(f )
mathend000# é o filtro vestigial tendo, a título de exemplo, a resposta em frequência da figura 5.5. Substituindo (5-4.3) em (5-4.2) obtemos
m'(t) = 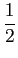 [m(t) + 2 [m(t) + 2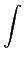 H H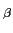 (f )M(f )ej2 (f )M(f )ej2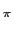 ftdf - j ftdf - j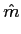 (t)], (t)], |
(5-4.04) |
o que se pode escrever no domínio da frequência
| M'(f ) |
= |
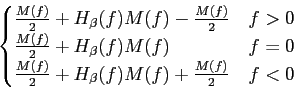 |
|
| |
= |
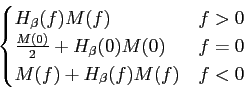 |
(5-4.05) |
e dado que o filtro vestigial tem o valor 1/2 para f = 0
mathend000# temos que
M'(f )= 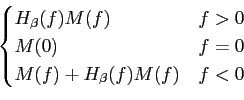 |
(5-4.06) |
o que permite escrever o espectro do sinal modulado
S'(f )= ![\begin{displaymath}\begin{cases}
{A_c\over 2}\{[1+H_\beta(f+f_c)]M(f+f_c)+ [1+H...
...f_c) + H_\beta(f-f_c)M(f-f_c)] & \vert f \vert > f_c\end{cases}\end{displaymath}](img294.png) |
(5-4.07) |
onde podemos apreciar que o espectro do sinal modulador para f = 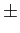 fc
mathend000# é mantido e que para f > fc
mathend000# e f < - fc
mathend000# é não nulo e apresenta uma resposta ``vestigial''
H
fc
mathend000# é mantido e que para f > fc
mathend000# e f < - fc
mathend000# é não nulo e apresenta uma resposta ``vestigial''
H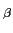 (f )M(f )
mathend000# de largura de banda
(f )M(f )
mathend000# de largura de banda 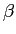 mathend000#. Podemos ainda constatar que se
mathend000#. Podemos ainda constatar que se
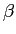
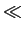 W
mathend000# então VSB aproxima-se de SSB, enquanto que se
W
mathend000# então VSB aproxima-se de SSB, enquanto que se
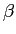
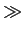 W
mathend000#, VSB tende para DSB.
W
mathend000#, VSB tende para DSB.
A potência transmitida Ps
mathend000# não é fácil de calcular mas encontra-se limitada por
dependendo da largura de banda vestigial 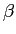 mathend000#.
mathend000#.
A última técnica de modulação em amplitude é denominada modulação de amplitude em quadratura (QAM - quadrature amplitude modulation). Neste caso dois sinais temporais e reais a(t)
mathend000# e b(t)
mathend000# formam o sinal modulador
m(t) = 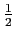 [a(t) + jb(t)]
mathend000#. Assim o sinal modulado escreve-se
[a(t) + jb(t)]
mathend000#. Assim o sinal modulado escreve-se
s(t) = Acm(t)cos(2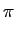 fct). fct). |
(5-5.01) |
O sinal passa banda resultante não é nem analítico nem tem simetria complexo conjugada em torno a f = fc
mathend000#. O sinal tem, em geral, bandas laterais superior e inferior sem simetria em torno à frequência da portadora. Escreve-se neste caso a partir de (5-5.1)
| s(t) |
= |
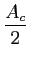 Re{[a(t) + jb(t)]ej Re{[a(t) + jb(t)]ej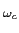 t} t} |
|
| |
= |
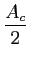 a(t)cos( a(t)cos(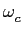 t) - t) - 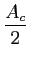 b(t)sin( b(t)sin(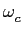 t), t), |
(5-5.02) |
de onde provém a denominação de modulação de amplitude em quadratura (QAM) visto tratarem-se de dois sinais modulados independentemente, à mesma frequência, mas com uma desfasagem relativa de 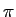 /2
mathend000#. Em termos de banda passante, e para a mesma banda de base, a modulação QAM requere a mesma banda que AM-DSB e o dobro da de AM-SSB, porém permite enviar dois sinais reais portadores de informação. A sua eficácia é portanto equivalente à de AM-SSB porém sem a sua dificuldade de implementação prática. QAM tornou-se por isso uma das técnicas de modulação mais utilizadas em sistemas de comunicação analógica (e não só).
/2
mathend000#. Em termos de banda passante, e para a mesma banda de base, a modulação QAM requere a mesma banda que AM-DSB e o dobro da de AM-SSB, porém permite enviar dois sinais reais portadores de informação. A sua eficácia é portanto equivalente à de AM-SSB porém sem a sua dificuldade de implementação prática. QAM tornou-se por isso uma das técnicas de modulação mais utilizadas em sistemas de comunicação analógica (e não só).
Modulação de ângulo é um termo genérico para designar um tipo de modulação na qual o ângulo da portadora sinusoidal varia em função do sinal modulador, i.e.,
s(t) = Accos[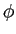 (t)], (t)], |
(5-6.01) |
onde a fase
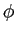 (t) = f[m(t)]
mathend000#, sendo m(t)
mathend000# o sinal modulador. Dois casos são possíveis na modulação de ângulo, que são: a modulação de fase (phase modulation, PM) e a modulação de frequência (frequency modulation, FM). Em termos práticos a modulação de ângulo tem como vantagem a de a portadora manter uma amplitude constante, o que a torna mais eficiente em termos de potência transmitida no emissor, e também de ser mais imune ao ruído. É o caso bem conhecido da qualidade superior do rádio FM em relação a AM.
(t) = f[m(t)]
mathend000#, sendo m(t)
mathend000# o sinal modulador. Dois casos são possíveis na modulação de ângulo, que são: a modulação de fase (phase modulation, PM) e a modulação de frequência (frequency modulation, FM). Em termos práticos a modulação de ângulo tem como vantagem a de a portadora manter uma amplitude constante, o que a torna mais eficiente em termos de potência transmitida no emissor, e também de ser mais imune ao ruído. É o caso bem conhecido da qualidade superior do rádio FM em relação a AM.
No caso da modulação de fase, 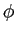 (t)
mathend000# escreve-se
(t)
mathend000# escreve-se
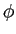 (t) = 2 (t) = 2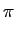 fct + fct + 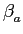 m(t), m(t), |
(5-6.02) |
onde 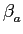 mathend000# é a constante de modulação de fase, que se encontra ligada ao índice de modulação ka
mathend000# por
mathend000# é a constante de modulação de fase, que se encontra ligada ao índice de modulação ka
mathend000# por
ka = 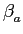 max|m(t)|. max|m(t)|. |
(5-6.03) |
No caso da modulação de frequência, que abordaremos mais em profundidade devido à sua importância prática, 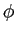 (t)
mathend000# escreve-se
(t)
mathend000# escreve-se
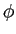 (t) = 2 (t) = 2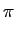 fct + 2 fct + 2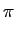 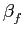 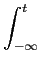 m( m( )d )d , , |
(5-6.04) |
onde 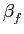 mathend000# é a constante de modulação e m(t)
mathend000# é sempre o sinal modulador. Podemos assim definir a frequência instantânea
mathend000# é a constante de modulação e m(t)
mathend000# é sempre o sinal modulador. Podemos assim definir a frequência instantânea
fi = 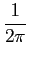 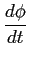 = fc + = fc + 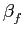 m(t), m(t), |
(5-6.05) |
e em geral define-se o índice de modulação como sendo
kf = 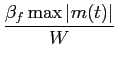 , , |
(5-6.06) |
onde W
mathend000# é a largura de banda de m(t)
mathend000#. Neste caso, se a mensagem m(t)
mathend000# for tal que
|m(t)|< 1
mathend000#, então podemos dizer que a constante 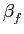 mathend000# corresponde à excursão máxima em frequência em torno à portadora fc
mathend000#. Isto levaria a pensar que a largura de banda ocupada pelo sinal modulado em FM seria na ordem de 2
mathend000# corresponde à excursão máxima em frequência em torno à portadora fc
mathend000#. Isto levaria a pensar que a largura de banda ocupada pelo sinal modulado em FM seria na ordem de 2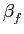 mathend000# o que, se fosse verdade, seria extraordinário, pois quereria dizer que a largura de banda do sinal modulado seria independente da largura de banda do sinal modulador !... O que obviamente é impossível. Vejamos o caso particular de um sinal modulador sinusoidal
m(t) = cos(
mathend000# o que, se fosse verdade, seria extraordinário, pois quereria dizer que a largura de banda do sinal modulado seria independente da largura de banda do sinal modulador !... O que obviamente é impossível. Vejamos o caso particular de um sinal modulador sinusoidal
m(t) = cos(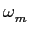 t)
mathend000#,
t)
mathend000#,
s(t) = Accos[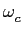 t + 2 t + 2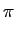 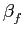 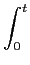 cos( cos(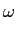  )d )d ], ], |
(5-6.07) |
e portanto
| s(t) |
= |
Accos[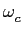 t + t + 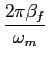 sin( sin(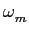 t)] t)] |
|
| |
= |
Accos[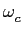 t + t + 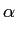 sin( sin(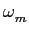 t)], t)], |
(5-6.08) |
onde
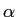 =
= 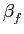 /fm
mathend000# é o rácio entre o desvio máximo em frequência
/fm
mathend000# é o rácio entre o desvio máximo em frequência 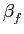 mathend000# e a frequência do sinal modulador. O sinal modulado pode ainda exprimir-se como
mathend000# e a frequência do sinal modulador. O sinal modulado pode ainda exprimir-se como
u(t) = 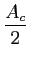 ej ej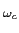 tej tej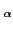 sin( sin(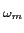 t) + t) + 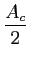 e-j e-j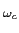 te-j te-j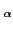 sin( sin(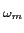 t). t). |
(5-6.09) |
Considerando, por exemplo, apenas o termo de frequência positiva podemos dizer que, tratando-se de uma função periódica de pulsação 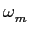 mathend000#, este se pode escrever sob forma de uma expansão em série de Fourier do tipo
mathend000#, este se pode escrever sob forma de uma expansão em série de Fourier do tipo
ej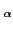 sin( sin(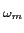 t) = t) = 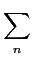 Cnejn Cnejn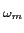 t, t, |
(5-6.10) |
onde os coeficientes Cn
mathend000# dependem do coeficiente 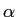 mathend000#. Esta relação entre Cn
mathend000# e
mathend000#. Esta relação entre Cn
mathend000# e 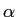 mathend000# não é simples, mas pode-se demonstrar que se escreve como
mathend000# não é simples, mas pode-se demonstrar que se escreve como
Cn = Jn(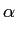 ), ), |
(5-6.11) |
onde
Jn(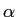 )
mathend000# é a função de Bessel de
)
mathend000# é a função de Bessel de 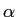 mathend000# de ordem n
mathend000# (ver [4]). Na prática podemos dizer que o espectro do sinal modulado se encontra centrado em + fc
mathend000# e - fc
mathend000#. Em torno a cada um destes valores o espectro do sinal m(t)
mathend000# estende-se em linhas a frequências múltiplas e sub-múltiplas de fm
mathend000# com amplitudes que dependem de (5-6.11). Em princípio a decomposição em série de Fourier (5-6.10) tem um número infinito de termos. Porém na prática
|Cn|
mathend000# decresce rapidamente para
|n|>
mathend000# de ordem n
mathend000# (ver [4]). Na prática podemos dizer que o espectro do sinal modulado se encontra centrado em + fc
mathend000# e - fc
mathend000#. Em torno a cada um destes valores o espectro do sinal m(t)
mathend000# estende-se em linhas a frequências múltiplas e sub-múltiplas de fm
mathend000# com amplitudes que dependem de (5-6.11). Em princípio a decomposição em série de Fourier (5-6.10) tem um número infinito de termos. Porém na prática
|Cn|
mathend000# decresce rapidamente para
|n|> 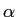 mathend000# e considerar apenas uma banda
mathend000# e considerar apenas uma banda
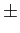 (1 +
(1 + 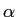 )fm
mathend000# é suficiente em termos práticos. Assim a banda total do sinal modulado escreve-se
)fm
mathend000# é suficiente em termos práticos. Assim a banda total do sinal modulado escreve-se
W = 2fm(1 + 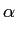 ) = 2fm +2 ) = 2fm +2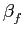 , , |
(5-6.12) |
e por isso é igual a duas vezes a excursão máxima em frequência mais duas vezes a banda do sinal modulador. Apesar de não se tratar de uma demonstração rigorosa podemos deduzir que a banda útil de um sinal modulado em FM é aproximadamente
W = 2B + 2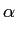 , , |
(5-6.13) |
onde B
mathend000# é a banda do sinal modulador.
Figura 5.6:
croquis de um sistema de multiplexagem temporal.
|
|
A multiplexagem é uma técnica que permite enviar várias mensagens distintas através do mesmo canal de transmissão simultaneamente. A multiplexagem pode fazer-se seja no tempo seja na frequência. No tempo torna-se óbvio que o envio de N
mathend000# mensagens pelo mesmo canal requere um canal de transmissão cujo bit/rate é pelo menos N x
mathend000# o bit rate de cada um dos canais. Na realidade o bit rate total será sempre superior a esse número pois torna-se necessária a inclusão de bits de controlo, de correcção de erros, de identificação dos canais, etc... Um dispositivo mecânico básico que exemplifica a multiplexagem temporal encontra-se representado na figura 5.2. Na prática a multiplexagem temporal é efectuada electronicamente por dispositivos de comutação.
Figura 5.7:
multiplexagem frequencial (FDM).
|
|
Mais importante, e mais utilizada, do que a multiplexagem temporal é a multiplexagem em frequência (frequency division multiplexing, FDM). A figura 5.7 exemplifica um tal sistema. Cada uma das mensagens é modulada em amplitude a uma frequência portadora diferente. Em seguida os sinais de cada um dos canais são somados e enviados no canal de transmissão. Torna-se óbvio que, para cada uma das mensagens possa ser recuperada intacta no receptor (desmultiplexagem), será necessaário que não exista sobreposição entre espectros contíguos, i.e., que a separação entre as frequências das portadoras de cada uma das mensagens seja superior ou igual à largura de banda das mesmas mensagens. Foram definidas normas para a transmissão de canais telefónicos que agrupam linhas em bandas de frequências conforme os números de canais desejados (tabela 5.2).
Tabela 5.2:
hierarquia de FDM publicada pela CCITT.
|
| Canal |
|
1 canal (4kHz) |
| Grupo |
|
12 canais (48 kHz) |
| Supergrupo |
5 grupos |
60 canais (240kHz) |
| Mastergrupo |
5 supergrupos |
300 canais (1.2 MHz) |
| Supermastergrupo |
3 mastergrupos |
900 canais (3.6 MHz) |
|
Frequentemente utiliza-se uma técnica de modulação eficiente, tipo AM-SSB, em cada um dos canais introduzidos no FDM e depois o sinal composto obtido é de novo modulado, utilizando por exemplo uma modulação FM, antes de transmissão intercontinental através de um canal de fibra óptica ou satélite.
Resumo do capítulo 5:
O último estágio do emissor que permite adaptar uma mensagem de tipo anal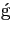 ico ao canal de comunicação é abordado neste capítulo através dos seguintes aspectos:
ico ao canal de comunicação é abordado neste capítulo através dos seguintes aspectos:
- modulação de amplitude dupla banda e banda única, sendo que em ambos os casos são tratados vários sub-casos; os casos com portadora e sem portadora na banda dupla, os casos de banda superior, banda inferior e vestigial na band lateral única. Para cada um dos casos é dada a expressão do sinal modulado no tempo e na frequência assim como a sua eficiência em termos de potência.
- depois em tratado com algum detalhe, devido à sua importância na prática, o caso da modulação da modulação de amplitude em quadratura (QAM) que faz aparecer desde logo a noção de separação da informação em amplitude e em fase (ou ângulo);
- aborda-se ainda o caso importante da modulação de ângulo seja para o caso da fase seja para o caso da modulação em frequência - esta última tratada com alguma atenção;
- finalmente aborda-se a multiplexagem no tempo e na frequência tomando como exemplo o caso do canal telefónico.
Sergio Jesus
2008-12-30
![]() fct)
fct)
![]() a
a![]() 1
1
![]() (t)
(t)
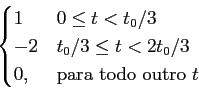
![]() (t)
(t)
![]() (t)
(t)
![]() (t) =
(t) = 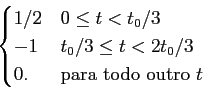
![]() (t) =
(t) = ![]() p
p![]()
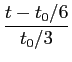
![]() - p
- p![]()
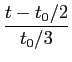
![]() ,
,
![]() (t)]cos(500
(t)]cos(500![]() t)
t)![$\displaystyle {2\left[1+0.4 p\left({{t-t_0/6}\over {t_0/3}}\right) -
0.8 p\left({{t-t_0/2}\over {t_0/3}}\right)\right]\cos(500\pi t)}$](img253.png) .
.![]()
![]() p
p![]()
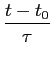
![]()
![]() =
= ![]() e-j2
e-j2![]() ft0sinc(f
ft0sinc(f![]() ),
),
![]() (t)
(t)
![]() (f )
(f )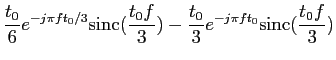
![$\displaystyle {{t_0\over 3}e^{-j\pi ft_0/3}{\rm sinc}({{t_0f}\over 3})
[1/2-e^{-j2\pi ft_0/3}]}$](img260.png) .
.![]() (f-fc)+
(f-fc)+![]() (f+fc)+
(f+fc)+![$\displaystyle {0.8{t_0\over 3}e^{-j\pi (f-f_c)t_0/3}{\rm sinc}
({{t_0(f-f_c)}\over 3})[1/2-e^{-j2\pi (f-f_c)t_0/3}] +}$](img261.png)
![$\displaystyle {0.8{t_0\over 3}e^{-j\pi (f+f_c)t_0/3}{\rm sinc}
({{t_0(f+f_c)}\over 3})[1/2-e^{-j2\pi (f+f_c)t_0/3}]}$](img262.png) ,
,![]() (t)
(t)
![]()
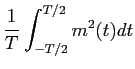
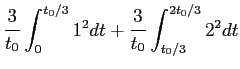
![]() =
= ![]() =
= ![]() .
.
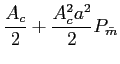
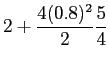
![]() fct)
fct)
![]() (t)Accos
(t)Accos![]() t + Accos
t + Accos![]() t
t![]() (t)]cos
(t)]cos![]() t.
t.![]() (t)
(t)
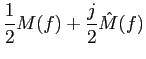
![]() Ac[m(t)cos
Ac[m(t)cos![]() t
t![]()
![]() (t)sin
(t)sin![]() t],
t],![]() t
t
![]() t - 90o)
t - 90o)
![]() (t)
(t)
![]() (t)
(t)
![]() (f )
(f )
![]() fc
fc
![]() (f )M(f )
(f )M(f )
![]()
![]()
![]() W
W
![]()
![]() W
W
![]() Ac2Pm
Ac2Pm![]() Ps
Ps![]()
![]() Ac2Pm,
Ac2Pm,![]()
![]() [a(t) + jb(t)]
[a(t) + jb(t)]
![]() /2
/2
![]() (t) = f[m(t)]
(t) = f[m(t)]
![]() (t)
(t)
![]()
![]() (t)
(t)
![]()
![]()
![]()
![]() t)
t)
![]() =
= ![]() /fm
/fm
![]()
![]()
![]()
![]()
![]() )
)
![]()
![]()
![]() (1 +
(1 + ![]() )fm
)fm
![]() ico ao canal de comunicação é abordado neste capítulo através dos seguintes aspectos:
ico ao canal de comunicação é abordado neste capítulo através dos seguintes aspectos:
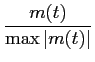 .
.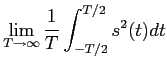
![$\displaystyle {\lim_{T \to \infty} {1\over T}\int_{-T/2}^{T/2} A_c^2[1+a\bar m(t)]^2 \cos^2(2\pi ft) dt}$](img264.png)
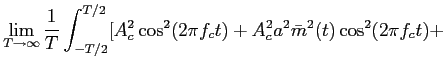
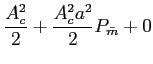 ,
,![\includegraphics[width=8cm]{figs/prod_modul.eps}](img275.png)
![\includegraphics[width=12cm]{figs/fig5-1.eps}](img276.png)
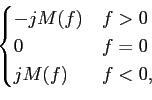
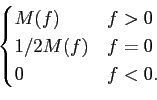
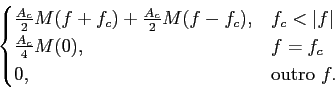
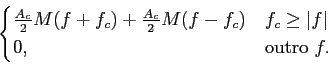
![\includegraphics[width=10cm]{figs/SSB1.eps}](img285.png)
![\includegraphics[width=10cm]{figs/SSB2.eps}](img286.png)
![\includegraphics[width=8cm]{figs/vsb_filter.eps}](img288.png)
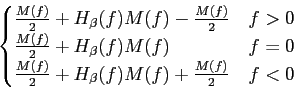
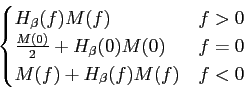
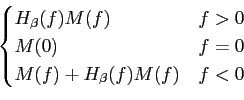
![\begin{displaymath}\begin{cases}
{A_c\over 2}\{[1+H_\beta(f+f_c)]M(f+f_c)+ [1+H...
...f_c) + H_\beta(f-f_c)M(f-f_c)] & \vert f \vert > f_c\end{cases}\end{displaymath}](img294.png)
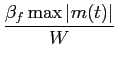 ,
,![\includegraphics[width=12cm]{figs/fig5-2.eps}](img313.png)
![\includegraphics[width=12cm]{figs/fig5-3.eps}](img314.png)