Subsections
Sinais e sistemas de comunicações
Num sistema de comunicações a mensagem é transmitida da fonte para o receptor através do canal de transmissão graças a um sistema emissor do lado da fonte e a um sistema receptor do lado do receptor. A informação a transmitir é codificada na fonte sob a forma de um sinal que é geralmente uma voltagem. A variação dessa voltagem ao longo do tempo contém a informação desejada - diz-se que o sinal serve de suporte da informação.
Geralmente, a tensão variável emitida na fonte é uma tensão, dita, analógica, i.e., o sinal pode ser representado por uma função de variável real do tempo, v(t)
mathend000#, se bem que hoje em dia existam já uma grande quantidade de fontes de informação discretas por natureza. No entanto, grande parte dos sistemas de comunicação modernos efectuam operações em sinais sob forma discreta e por isso seremos levados a manipular seja sinais contínuos seja discretos. A emissão de um sinal modulado num dado canal de
transmissão requer normalmente a utilização de uma banda de frequência em torno a uma portadora. De modo a facilitar a caracterização dos sistemas de emissão e de recepção e sem perda de generalidade os sinais passa-banda são transformados nos seus equivalentes passa-baixo de forma a tornar o sistema independente da banda de frequências de tranmissão.
Modulação e sinais passa-banda
Figura 2.1:
espectro do sinal original.
|
|
Consideremos um sinal x(t)
mathend000#, passa-baixo, com uma banda limitada, tendo um espectro
|X(f )|
mathend000# que é nulo fora de uma banda (- W, W)
mathend000# (ver figura 2.1). Num problema de comunicações servimo-nos em geral de uma portadora de frequência 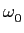 mathend000#, de tal modo que o sinal modulado é
mathend000#, de tal modo que o sinal modulado é
v(t) = x(t)cos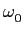 t, t, 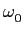 = 2 = 2 f0 f0 |
(2-1.01) |
Como sabemos que a representação frequencial de
cos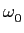 t
mathend000# é constituída por dois Diracs colocados em
t
mathend000# é constituída por dois Diracs colocados em
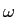 = -
= - 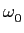 mathend000# e em
mathend000# e em
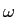 =
= 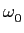 mathend000# o produto temporal da (2-1.1) torna-se numa convolução no domínio da frequência. O resultado é
mathend000# o produto temporal da (2-1.1) torna-se numa convolução no domínio da frequência. O resultado é
V(f )= X(f ) * TF[cos(2 f0t)] = f0t)] =  X(f + f0) + X(f + f0) +  X(f - f0) X(f - f0) |
(2-1.02) |
Isto está ilustrado na figura 2.2. Este resultado que serve de introdução à problemática da modulação e à noção de sinais passa-banda tem dois aspectos interessantes: 1) é que a simples multiplicação de um sinal por uma sinusoide tem por efeito a deslocação na frequência desse sinal duma quantidade igual à frequência da sinusoide e 2) constata-se facilmente que para que o sinal modulador mantenha o seu espectro intacto a frequência da sinusoide (normalmente chamada ``portadora'') tem de ser igual ou superior a duas vezes a largura de banda do sinal modulador, i.e.,
fs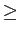 2W
mathend000#.
2W
mathend000#.
Figura 2.2:
espectro do sinal modulado.
|
|
Sinais e sistemas passa-banda e a transformada de Hilbert
Como já tivemos a ocasião de mencionar na introdução, um dos papéis desempenhados pelos sistemas de comunicação colocados no emissor, é o de adaptar o sinal ao canal de comunicação. Frequentemente, uma das características essenciais do canal de comunicação é de que a sua banda de frequências é limitada em torno a um determinado valor: dizemos que se trata de um canal ''passa-banda'' - é o caso do canal rádio-frequência. O sistema de comunicação emissor terá então de transformar o sinal contendo a mensagem a emitir num sinal passa-banda compatível com o canal de transmissão. Vamos agora descrever o formalismo matemático que permite representar sinais passa-banda e a sua manipulação ao longo da cadeia de transmissão.
Vamos considerar o sinal passa-banda s(t)
mathend000# com o espectro S(f )
mathend000#. Primeiramente vamos considerar um novo sinal que contenha apenas a parte positiva do espectro de s(t)
mathend000#,
| S+(f )= 2u(f )S(f ), |
(2-2.01) |
onde u(f )
mathend000# é a função degrau unidade e o factor 2 tem em conta a conservação da energia, i.e., S+(f )
mathend000# e S(f )
mathend000# têm a mesma energia. No domínio do tempo temos
| s+(t) |
= |
 S+(f )ej2 S+(f )ej2 ftdf, ftdf, |
(2-2.02) |
| |
= |
TF-1[2u(f )] * TF-1[S(f )]. |
(2-2.03) |
Visto que (ver apêndice A.1)
TF-1[2u(f )] = 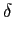 (t) + (t) + 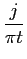 , , |
(2-2.04) |
temos
s+(t) =  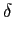 (t) + j (t) + j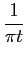 ![$\displaystyle \left.\vphantom{\delta(t) + j {1\over {\pi t}}}\right]$](img38.png) * s(t). * s(t). |
(2-2.05) |
O sinal s+(t)
mathend000# é chamado pre-envelope ou sinal analítico de s(t)
mathend000#, e não é mais do que uma versão complexa de s(t)
mathend000#, cuja parte real é o próprio s(t)
mathend000# e a parte imaginária é a Transformada de Hilbert de s(t)
mathend000#, que definimos de seguida. O sistema cuja resposta em frequência se comporta como uma funçõ degrau u(f )
mathend000# da (2-2.1) é normalmente chamado ``phase splitter'' e tem como resposta impulsiva
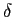 (t) + j/
(t) + j/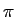 t
mathend000#. Assim a resposta do ``phase splitter'' é o sinal analítico.
t
mathend000#. Assim a resposta do ``phase splitter'' é o sinal analítico.
Transformada de Hilbert
A partir do segundo termo do segundo membro de (2-2.5) define-se
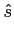 (t) (t) |
= |
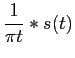 , , |
(2-2.06) |
| |
= |
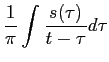 , , |
(2-2.07) |
como sendo a Transformada de Hilbert de s(t)
mathend000#, cuja notação é
Uma forma alternativa de ver a transformada de Hilbert é de considerar que o sinal 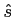 (t)
mathend000# pode ser visto como o sinal de saída de um filtro cuja resposta impulsiva é
(t)
mathend000# pode ser visto como o sinal de saída de um filtro cuja resposta impulsiva é
h(t) = 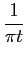 , - , - 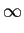 < t < < t < 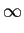 |
(2-2.09) |
excitado pelo sinal s(t)
mathend000# à entrada. Este filtro é então chamado um transformador de Hilbert e a sua resposta em frequência escreve-se
H(f )= TF[h(t)] = - jsgn(f )= 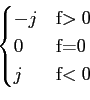 . . |
(2-2.10) |
Podemos notar que a função de transferência do filtro de Hilbert é tal que o seu módulo é
|H(f )|= 1
mathend000# (salvo para o ponto f = 0
mathend000#) e a sua fase é
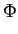 (f )= (f )= 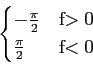 , , |
(2-2.11) |
o que nos faz dizer que este filtro se comporta como um desfasador puro de 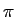 /2
mathend000# para todas as frequências do sinal de entrada, enquanto a amplitude não é alterada.
/2
mathend000# para todas as frequências do sinal de entrada, enquanto a amplitude não é alterada.
Propriedades
porventura a propriedade mais útil na manipulação da TH é o cálculo da sua TF. Dado (2-2.6) podemos escrever a TF da TH como
TF[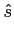 (t)] (t)] |
= |
TF[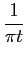 * s(t)], * s(t)], |
|
| |
= |
TF 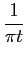 ![$\displaystyle \left.\vphantom{{1\over {\pi t}}}\right]$](img51.png) S(f ), S(f ), |
|
| |
= |
- jsgn(f )S(f ), |
(2-2.12) |
resultado que utilizaremos abundantemente a seguir.
a transformada de Hilbert de uma constante é zero, i.e.,
 |
= |
TH[c] |
|
| |
= |
![$\displaystyle {c \ast \left[ {1\over {\pi t}} \right]}$](img53.png) |
(2-2.13) |
calculando a TF de ambos os termos
TF[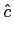 ] = c ] = c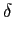 (f )[- jsgn(f )] = 0. (f )[- jsgn(f )] = 0. |
(2-2.14) |
e portanto a sua TF-1
mathend000# é igualmente nula.
calculando a transformada de Hilbert duas vezes permite obter o negativo do sinal original,
calculando a TF
TF[TH[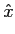 (t)]] (t)]] |
= |
X(f )[- jsgn(f )][- jsgn(f )] |
|
| |
= |
- X(f ) |
(2-2.16) |
e daí
mathend000# o resultado procurado.
demonstra-se facilmente que um sinal x(t)
mathend000# e a sua TH, 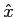 (t)
mathend000# são ortogonais. Com efeito tirando partido da generalização do teorema de Parseval podemos escrever que
(t)
mathend000# são ortogonais. Com efeito tirando partido da generalização do teorema de Parseval podemos escrever que
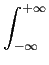 x(t) x(t)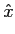 (t) * dt = (t) * dt = 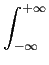 X(f ) X(f )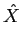 (f ) * df (f ) * df |
(2-2.17) |
e portanto
 x(t) x(t)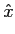 (t) * dt (t) * dt |
= |
 X(f )[jsgn(f )X * (f )]df X(f )[jsgn(f )X * (f )]df |
|
| |
= |
-j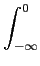 X(f )X * (f )df+j X(f )X * (f )df+j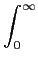 X(f )X * (f )df X(f )X * (f )df |
|
| |
= |
0. |
(2-2.18) |
no caso em que x(t)
mathend000# é real, o que implica que o seu espectro de potência é simétrico na frequência e assim a energia na parte negativa do espectro é igual à energia na parte positiva.
a TH do produto de convolução escreve-se
| TH[x(t) * h(t)] |
= |
x(t) * h(t) * 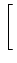 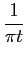 ![$\displaystyle \left.\vphantom{{1\over {\pi t}}}\right]$](img51.png) |
|
| |
= |
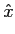 (t) * h(t) (t) * h(t) |
|
| |
= |
x(t) * 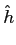 (t). (t). |
(2-2.19) |
Exemplo 2.1: calcular a TH do sinal
x(
t) = exp(
j t
t)
mathend000#
é fácil de determinar que
TF[TH[exp(j t)]] t)]] |
= TF[exp(j t)][- jsgn(f )] t)][- jsgn(f )] |
| |
= - j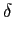 (f - fc)sgn(f ) (f - fc)sgn(f ) |
mathend000#
e daí
mathend000# que calculando a TF-1
mathend000# desta expressão se obtenha o resultado pretendido
| TH[x(t)] |
=  -jsgn(f ) -jsgn(f )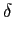 (f-fc)exp(j2 (f-fc)exp(j2 ft)df ft)df |
| |
= - jsgn(fc)exp(j t). t). |
mathend000#
finalmente podemos deduzir do resultado precedente que
TH[exp(
j t
t +

)] = -
jsgn(
fc)exp(
j t
t +

).
mathend000#
ainda a partir deste resultado podemos facilmente deduzir que
TH[cos t] t] |
= |
sgn(fc)sin t, t, |
(2-2.20) |
TH[sin t] t] |
= |
- sgn(fc)cos t, t, |
(2-2.21) |
e também por combinação das relações precedentes
TH[cos( t + t +  )] )] |
= |
sgn(fc)sin( t + t +  ) ) |
(2-2.22) |
TH[sin( t + t +  )] )] |
= |
- sgn(fc)cos( t + t +  ). ). |
(2-2.23) |
Exemplo 2.2: calcular a TH do sinal
x(t) = b(t)exp(j t) t) |
(2-2.24) |
onde o sinal b(t)
mathend000# é uma função passa-baixo limitada dentro da banda espectral [- W, W]
mathend000#. Prova-se então que
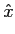 (t) = - jsgn(fc)b(t)exp(j (t) = - jsgn(fc)b(t)exp(j t) t) |
(2-2.25) |
onde se supõe que
|fc|> W
mathend000#. Deixamos a demonstração deste resultado como exercício para as aulas TP. Simultaneamente, tendo em conta os resultados acima, podemos escrever
TH[b(t)exp(j t + t +  )] = - jsgn(fc)b(t)exp(j )] = - jsgn(fc)b(t)exp(j t + t +  ). ). |
(2-2.26) |
Vamos agora supôr que temos duas funções passa-baixo xc(t)
mathend000# e xs(t)
mathend000# cujo espectro se encontra contido no intervalo
[- fc, fc]
mathend000# com fc > 0
mathend000#. Assim, combinando (2-2.20) - (2-2.21) com (2-2.25), podemos dizer que
TH[xc(t)cos t] t] |
= |
xc(t)sin t t |
(2-2.27) |
TH[xs(t)sin t] t] |
= |
- xs(t)cos t t |
(2-2.28) |
a partir das quais podemos ainda dizer que a TH de
x(t) = xc(t)cos t - xs(t)sin t - xs(t)sin t t |
(2-2.29) |
é dada por
| TH[x(t)] |
= |
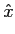 (t), (t), |
|
| |
= |
xc(t)sin t + xs(t)cos t + xs(t)cos t. t. |
(2-2.30) |
Se invertermos o sistema de equações (2-2.29) e (2-2.30) em relação a xc(t)
mathend000# e xs(t)
mathend000# podemos calcular as componentes do sinal x(t)
mathend000#
xc(t) = x(t)cos t + t + 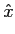 (t)sin (t)sin t t |
|
|
(2-2.31) |
xs(t) = 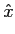 (t)cos (t)cos t - x(t)sin t - x(t)sin t t |
|
|
(2-2.32) |
se um dado sinal x(t)
mathend000# não tem nenhuma componente constante (DC) então a sua energia é conservada pela TH. Com efeito
 |x(t) |x(t) dt = dt =  | |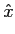 (t) (t) dt. dt. |
(2-2.33) |
Deixamos a demonstração como exercício.
Se o sinal analítico s+(t)
mathend000# for um sinal passa-banda, i.e., tomar valores diferentes de zero para uma banda de frequências em torno a uma frequência fc
mathend000#, e for zero para todos os outros valores de f
mathend000#, para colocar o sinal s+(t)
mathend000# em banda base, i.e., numa banda de frequências em torno a f = 0
mathend000#, teremos de fazer uma translação de fc
mathend000# Hz. Assim o sinal em banda base equivalente a s+(t)
mathend000# será (no domínio da frequência)
Sbb(f )= S+(f + fc)
mathend000# ou seja no tempo
| sbb(t) |
= |
s+(t)e-j2 fct fct |
|
| |
= |
[s(t)+j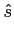 (t)]e-j2 (t)]e-j2 fct fct |
(2-2.34) |
e de forma equivalente
[s(t) + j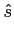 (t)] = sbb(t)ej2 (t)] = sbb(t)ej2 fct, fct, |
(2-2.35) |
de onde fazendo
sbb(t) = x(t) + jy(t)
mathend000# e igualando partes reais e imaginárias de (2-2.35) obtemos
| s(t) |
= |
x(t)cos(2 fct) - y(t)sin(2 fct) - y(t)sin(2 fct), fct), |
(2-2.36) |
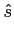 (t) (t) |
= |
x(t)sin(2 fct) + y(t)cos(2 fct) + y(t)cos(2 fct). fct). |
(2-2.37) |
A equação (2-2.36) é uma representação do sinal passa-banda s(t)
mathend000# no qual as suas componentes em banda-base x(t)
mathend000# e y(t)
mathend000# se encontram como moduladoras do cos
mathend000# e do sin
mathend000# às frequências centrais fc
mathend000#; x(t)
mathend000# e y(t)
mathend000# são chamadas as componentes em fase e em quadratura do sinal s(t)
mathend000# visto que as funções que elas modulam estão desfasadas de 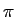 /2
mathend000#. Utilizando (2-2.35) podemos escrever o sinal em banda s(t)
mathend000# como sendo
/2
mathend000#. Utilizando (2-2.35) podemos escrever o sinal em banda s(t)
mathend000# como sendo
| s(t) |
= |
Re[sbb(t)ej2 fct], fct], |
(2-2.38) |
| |
= |
Re{[x(t) + jy(t)]ej2 fct}, fct}, |
|
onde Re
mathend000# significa ``parte real de''. Resumindo, partindo de um sinal real em banda-passante s(t)
mathend000# o seu equivalente passa-baixo em banda de base é sbb(t)
mathend000# dado por (2-2.34) e, vice-versa, o sinal em banda passante s(t)
mathend000# pode ser obtido a partir da sua representação em banda basesbb(t)
mathend000# usando (2-2.39). Alternativamente, utilizando a representação exponencial dum número complexo, podemos escrever
sbb(t) = a(t)ej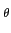 (t), (t), |
(2-2.39) |
onde
| a(t) |
= |
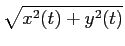 , , |
(2-2.40) |
 (t) (t) |
= |
tan-1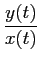 , , |
(2-2.41) |
e onde a(t)
mathend000# e 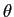 (t)
mathend000# são chamados o envelope e a fase de s(t)
mathend000#, respectivamente. Assim, utilizando a definição (2-2.39),
(t)
mathend000# são chamados o envelope e a fase de s(t)
mathend000#, respectivamente. Assim, utilizando a definição (2-2.39),
| s(t) |
= |
Re{a(t)ej[2 fct+ fct+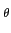 (t)]}, (t)]}, |
|
| |
= |
a(t)cos[2 fct + fct +  (t)]. (t)]. |
(2-2.42) |
A TF de s(t)
mathend000# escreve-se, utilizando mais uma vez (2-2.39)
S(f )=  Re[sbb(t)ej2 Re[sbb(t)ej2 fct]e-j2 fct]e-j2 ftdt, ftdt, |
(2-2.43) |
e sabendo que a parte real de um número complexo qualquer z
mathend000# se pode escrever como
| Re(z) = (1/2)[z + z * ], |
(2-2.44) |
então
| S(f ) |
= |
  [sbb(t)ej2 [sbb(t)ej2 fct + sbb * e-j2 fct + sbb * e-j2 fct]e-j2 fct]e-j2 ftdt, ftdt, |
|
| |
= |
 [Sbb(f - fc) + Sbb * (- f - fc)], [Sbb(f - fc) + Sbb * (- f - fc)], |
(2-2.45) |
que nos permite calcular o espectro S(f )
mathend000# do sinal passa-banda s(t)
mathend000# a partir do espectro Sbb(f )
mathend000# do seu equivalente passa-baixo sbb(t)
mathend000#. Note-se que
Sbb(f - fc)
mathend000# é simplesmente o espectro de sbb(t)
mathend000# deslocado de fc
mathend000# Hz no sentido das frequências positivas, enquanto
S * bb(- f - fc)
mathend000# é o complexo conjugado do espectro de sbb(t)
mathend000# invertido na frequência e deslocado de fc
mathend000# Hz no sentido das frequências negativas. Esta última afirmação é fácil de comprender se notarmos que
Sastbb(- f - fc) = S * bb[- (f + fc)]
mathend000#.
Uma notação semelhante pode ser utilizada para representar sistemas passa-banda de resposta impulsiva h(t)
mathend000#
h(t) = Re[hbb(t)ej2 fct], fct], |
(2-2.46) |
onde hbb(t)
mathend000# é o seu equivalente passa-baixo sendo que, normalmente, h(t)
mathend000# é real mas o seu equivalente passa-baixo hbb(t)
mathend000# é complexo. A função de transferência do sistema passa-banda escreve-se
H(f )=  [Hbb(f - fc) + Hbb * (- f - fc)], [Hbb(f - fc) + Hbb * (- f - fc)], |
(2-2.47) |
e onde
| Hbb(f - fc) |
= |
H+(f ), |
|
| |
= |
2u(f )H(f ), |
|
| |
= |
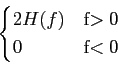 , , |
(2-2.48) |
é a componente para f > 0
mathend000# do espectro de H(f )
mathend000# e da mesma forma
H * bb(- f - fc) = 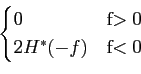 . . |
(2-2.49) |
Frequentemente o factor 2 é abandonado na representação de sistemas passa-banda, o que resulta no aparecimento de um factor 2 na equação (2-2.46) e no desaparecimento do factor 1/2 em (2-2.47). Deve-se aqui acrescentar que, visto que h(t)
mathend000# é real, então temos
| H(f )= H * (- f ). |
(2-2.50) |
A resposta r(t)
mathend000# de um sistema passa-banda de resposta impulsiva h(t)
mathend000# a um sinal passa-banda s(t)
mathend000# escreve-se normalmente como o produto de convolução
r(t) =  s( s( )h(t - )h(t -  )d )d , , |
(2-2.51) |
e de modo equivalente
| R(f )= H(f )S(f ), |
(2-2.52) |
onde por substituição
R(f )=  [Hbb(f - fc) + Hbb * (- f - fc)][Sbb(f - fc) + Sbb * (- f - fc)], [Hbb(f - fc) + Hbb * (- f - fc)][Sbb(f - fc) + Sbb * (- f - fc)], |
(2-2.53) |
onde se utilizaram as relações (2-2.45) e (2-2.47) (esta última sem o coeficiente 1/2).Se o sinal s(t)
mathend000# for de banda estreita, i.e., a sua banda útil B
mathend000# é tal que B 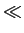 fc
mathend000# então poderemos dizer que
Sbb(f - fc)
fc
mathend000# então poderemos dizer que
Sbb(f - fc) 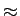 0
mathend000# para frequências negativas e o mesmo para o sistema passa-banda
Hbb(f - fc) = 0
mathend000# para f < 0
mathend000#. A relação (2-2.53) reduz-se então aos dois termos cruzados de resposta para frequências positivas,
0
mathend000# para frequências negativas e o mesmo para o sistema passa-banda
Hbb(f - fc) = 0
mathend000# para f < 0
mathend000#. A relação (2-2.53) reduz-se então aos dois termos cruzados de resposta para frequências positivas,
| R(f ) |
= |
 [Sbb(f - fc)Hbb(f - fc) + Sbb * (- f - fc)Hbb * (- f - fc)], [Sbb(f - fc)Hbb(f - fc) + Sbb * (- f - fc)Hbb * (- f - fc)], |
|
| |
= |
 [Rbb(f - fc) + Rbb * (- f - fc)], [Rbb(f - fc) + Rbb * (- f - fc)], |
(2-2.54) |
de onde podemos escrever que
| Rbb(f )= Hbb(f )Sbb(f ), |
(2-2.55) |
é o equivalente passa-baixo Rbb(f )
mathend000# da resposta do sistema passa-banda R(f )
mathend000#, dada como o produto das TFs dos equivalentes passa-baixo do sinal de entrada e do sistema. Esta relação permite-nos obviamente escrever
rbb(t) =  sbb( sbb( )hbb(t - )hbb(t -  )d )d . . |
(2-2.56) |
Energia e potência
A energia de um sinal é uma quantidade fundamental nos sistemas de comunicação. Assim definimos a energia de um sinal s(t)
mathend000# por
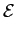 x = x =  |x(t) |x(t) dt, e dt, e 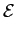 x = x = 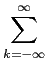 |xk |xk |
(2-2.57) |
para sinais contínuos e discretos respectivamente. Sendo a potência igual à energia por unidade de tempo, só poderemos calcular a potência contida num sinal como sendo a potência média dada por
Ps = 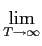 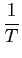 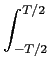 |s(t) |s(t) dt, e Ps = dt, e Ps = 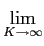 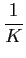 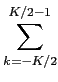 |sk |sk . . |
(2-2.58) |
Para sinais passa-banda, e utilizando a relação (2-2.44) no caso contínuo de (2-2.57), obtem-se
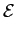 s s |
= |
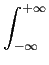 ![$\displaystyle \left[\vphantom{ {1\over 2} [s_{bb}(t)e^{j2\pi f_c t}+s_{bb}^{\ast}(t)e^{-j2\pi f_c t}] }\right.$](img82.png)  [sbb(t)ej2 [sbb(t)ej2 fct + sbb * (t)e-j2 fct + sbb * (t)e-j2 fct] fct]![$\displaystyle \left.\vphantom{ {1\over 2} [s_{bb}(t)e^{j2\pi f_c t}+s_{bb}^{\ast}(t)e^{-j2\pi f_c t}] }\right]^{2}_{}$](img83.png) dt dt |
|
| |
= |
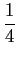 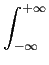 {2sbb(t)sbb * (t) + sbb2(t)ej4 {2sbb(t)sbb * (t) + sbb2(t)ej4 fct + [sbb * (t)]2e-j4 fct + [sbb * (t)]2e-j4 fct}dt. fct}dt. |
(2-2.59) |
Visto que
sbb(t)sbb * (t) =|sbb(t)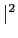 mathend000#, temos que
mathend000#, temos que
 s s |
= |
 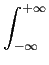 |sbb(t) |sbb(t) dt + dt +  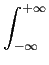 [ [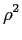 (t)ej2 (t)ej2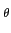 (t)ej4 (t)ej4 fct + fct + |
|
| |
|
+ 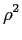 (t)e-j2 (t)e-j2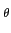 (t)e-j4 (t)e-j4 fct]dt, fct]dt, |
(2-2.60) |
onde se utilizou
sbb(t) = 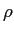 (t)e-j
(t)e-j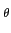 (t)
mathend000#, com
(t)
mathend000#, com
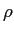 (t) =|sbb(t)|
mathend000# e
(t) =|sbb(t)|
mathend000# e
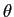 =
= 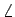 [sbb(t)]
mathend000#, e assim podemos escrever
[sbb(t)]
mathend000#, e assim podemos escrever
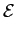 s s |
= |
 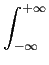 |sbb(t) |sbb(t) dt + dt + 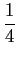 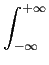 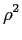 (t)[ej[4 (t)[ej[4 fct+2 fct+2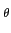 (t)] + e-j[4 (t)] + e-j[4 fct+2 fct+2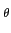 (t)]]dt, (t)]]dt, |
|
| |
= |
 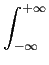 |sbb(t) |sbb(t) dt + dt +  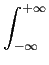 |sbb(t) |sbb(t) cos[4 cos[4 fct + 2 fct + 2 (t)]dt, (t)]dt, |
(2-2.61) |
onde, por definição, o sinal sbb(t)
mathend000# é passa-baixo comparado com a frequência fc
mathend000# e assim podemos dizer que o segundo termo desta expressão é um coseno que varia rapidamente, modulado lentamente em amplitude por sbb(t)
mathend000#. Baseando-nos na ideia de que o integral de um cos
mathend000# no intervalo
[- 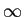 , +
, + 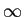 ]
mathend000# é zero, podemos assim dizer que o segundo termo em (2-2.61) é aproximadamente nulo o que nos dá que a energia é finalmente
]
mathend000# é zero, podemos assim dizer que o segundo termo em (2-2.61) é aproximadamente nulo o que nos dá que a energia é finalmente
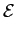 s s |
= |
 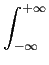 |sbb(t) |sbb(t) dt, dt, |
|
| |
= |
 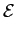 bb, bb, |
(2-2.62) |
onde
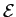 bb
mathend000# é a energia do sinal em banda base sbb(t)
mathend000#.
bb
mathend000# é a energia do sinal em banda base sbb(t)
mathend000#.
Representação espectral de sinais aleatórios
A passagem de um sinal através de um sistema físico de natureza electrónica (analógica ou digital) adiciona forçosamente uma componente aleatória indesejável, à qual chamamos ruído. Da mesma forma a passagem do sinal através de um canal de transmissão físico adiciona ruído de transmissão. A adição de uma componente de ruído aleatório num sinal determinístico resulta num sinal de natureza estocástica. Neste capítulo vamos generalizar as noções de sinais e sua representação espectral ao caso de sinais estocásticos. O aluno não familiar com as noções básicas de definição de processos estocásticos deverá rever a matéria de Probabilidades, Estatística e Processos Estocásticos.
Noções preliminares
Já vimos na disciplina de Sistemas e Sinais [5], que uma das condições de existência da TF é que o sinal em questão deverá ser absolutamente integrável, o que se pode representar por
 |s(x)|dx < |s(x)|dx < 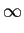 , , |
(2-3.01) |
que é uma condição de certo modo drástica e exclui, por exemplo, desde já, simples funções periódicas como sin(x)
mathend000#. O cálculo das TF de funções periódicas só pode ser feito exactamente através de Séries de Fourier (SF), ou então, através do uso da noção de função generalizada ou distribuição. Outra forma de resolver o problema na prática, é o de limitar o intervalo de integração de forma a torná-lo finito. Nesse caso, é possível obter um resultado, que não será a TF do sinal pretendido, mas sim a TF do sinal multiplicado pela função de observação (janela), que no caso determinístico pode ser determinada inequivocamente. Tudo isto já foi visto anteriormente e não será repetido. Outro tipo de sinais excluidos da TF, são os sinais ditos aleatórios que, em termos matemáticos, são apenas processos estocásticos. Mas neste caso o problema do cálculo é dificilmente solúvel de modo único pois que, mesmo para um intervalo de tempo limitado, uma nova realização do sinal produz uma nova TF e então devemos questionar-nos sobre qual o verdadeiro significado da representação espectral dum sinal aleatório. Na realidade o verdadeiro resultado não existe (ou pelo menos não pode ser calculado de forma inequívoca) e apenas temos acesso a estimativas desse resultado, e é nesse sentido que se fala de estimação espectral e não de cálculo espectral. Chegou a altura de apresentarmos um exemplo do problema enfrentado em estimação espectral.
consideremos o simples caso de um sinal sinusoidal
s(t) = cos(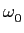 t)
mathend000#. Sabemos através da teoria que a TF de s(t)
mathend000# é
t)
mathend000#. Sabemos através da teoria que a TF de s(t)
mathend000# é
TF[s(t)] =  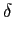 ( (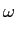 - - 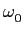 ) + ) +  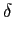 ( (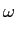 + + 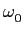 ) ) |
(2-3.02) |
Façamos agora o exercício já nosso conhecido que consiste em observar o sinal s(t)
mathend000# no intervalo finito [0, T]
mathend000#. Nesse caso temos que
| TF[s(t)] = TF{s(t)rect[(t - T/2)/T]} |
(2-3.03) |
e portanto, sabendo que a TF do rect é um sinc, o resultado vai ser duas funções sinc centradas em
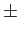
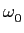 mathend000#. A largura do pico central e a amplitude dos picos laterais da função sinc vão ser proporcionais a 1/T
mathend000#. Na prática isto significa que, quanto maior for o intervalo de observação T
mathend000#, mais estreito vai ser o pico central do sinc e menores vão ser os picos laterais. Por outras palavras, passando ao limite, as funções sinc irão tender para Diracs. Tudo isto já foi visto anteriormente e diz respeito ao caso da observação dum sinal determinístico num intervalo finito.
mathend000#. A largura do pico central e a amplitude dos picos laterais da função sinc vão ser proporcionais a 1/T
mathend000#. Na prática isto significa que, quanto maior for o intervalo de observação T
mathend000#, mais estreito vai ser o pico central do sinc e menores vão ser os picos laterais. Por outras palavras, passando ao limite, as funções sinc irão tender para Diracs. Tudo isto já foi visto anteriormente e diz respeito ao caso da observação dum sinal determinístico num intervalo finito.
Vejamos agora o seguinte problema. Considere o sinal
y(t) = s(t) + n(t)
mathend000#, onde n(t)
mathend000# é uma sequência de ruído branco de média nula e variância
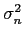 mathend000# e onde s(t)
mathend000# é o nosso sinal sinusoidal. Se a relação sinal/ruído for suficientemente baixa, uma simples inspecção de y(t)
mathend000# não será suficiente para determinar a presença de s(t)
mathend000# e muito menos a sua forma, amplitude ou frequência. Ocorre-nos então a ideia de recorrer à representação espectral de y(t)
mathend000# que, normalmente, deveria mostrar um máximo pronunciado para uma determinada frequência, se s(t)
mathend000# estivesse presente e a sua abcissa seria nem mais menos que o valor da frequência de s(t)
mathend000#,
mathend000# e onde s(t)
mathend000# é o nosso sinal sinusoidal. Se a relação sinal/ruído for suficientemente baixa, uma simples inspecção de y(t)
mathend000# não será suficiente para determinar a presença de s(t)
mathend000# e muito menos a sua forma, amplitude ou frequência. Ocorre-nos então a ideia de recorrer à representação espectral de y(t)
mathend000# que, normalmente, deveria mostrar um máximo pronunciado para uma determinada frequência, se s(t)
mathend000# estivesse presente e a sua abcissa seria nem mais menos que o valor da frequência de s(t)
mathend000#, 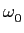 mathend000#. O primeiro problema é que a TF de y(t)
mathend000# - teoricamente pelo menos - não existe porque n(t)
mathend000# não é integrável entre
[-
mathend000#. O primeiro problema é que a TF de y(t)
mathend000# - teoricamente pelo menos - não existe porque n(t)
mathend000# não é integrável entre
[- 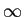 ,
,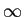 ]
mathend000#. Utilizamos então o caminho alternativo que é a função de correlação e que nos leva à densidade espectral. Assim
]
mathend000#. Utilizamos então o caminho alternativo que é a função de correlação e que nos leva à densidade espectral. Assim
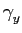 (t1, t2) = E[y(t1)y(t2)], (t1, t2) = E[y(t1)y(t2)], |
(2-3.04) |
onde E[ ]
mathend000# é o operador ``esperança matemática'' ou valor esperado. A questão complica-se pois, se para s(t)
mathend000# determinístico
E[s(t)] = s(t)
mathend000# para n(t)
mathend000# aleatório, são necessárias - sempre teoricamente - um número infinito de tiragens aleatórias. Além disso podemos questionar-nos sobre o sentido de calcular ``periodicidades'' de um sinal n(t)
mathend000# que não tem um ``comportamento mais ou menos constante'' em torno a um determinado valor médio. Em termos matemáticos, isto quer dizer que, para fazer algum sentido calcular o espectro de n(t)
mathend000#, este tem de ser estacionário1 (pelo menos no sentido lato) e ergódico2 de forma a podermos dizer que (pelo menos) os momentos de primeira e segunda ordem são independentes do instante de cálculo e que a média temporal é igual (no limite) à média de conjunto (ver noções de estacionaridade e ergodicidade em [5]). Assim, considerando que podemos obter um número infinito de tiragens aleatórias de y(t)
mathend000#, podemos escrever
onde
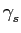 (
( )
mathend000# é suposto conhecido3 e
)
mathend000# é suposto conhecido3 e
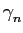 (
( ) =
) = 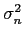
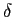 (
( )
mathend000#. A TF de (2-3.5) dá-nos, segundo a definição, a densidade espectral de y(t)
mathend000#,
)
mathend000#. A TF de (2-3.5) dá-nos, segundo a definição, a densidade espectral de y(t)
mathend000#,
Pyy(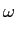 ) ) |
= |
TF[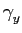 ( ( )] )] |
|
| |
= |
Pss(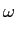 ) + ) + 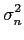 |
(2-3.06) |
o que nos diz que o efeito do ruído branco é o de adicionar uma constante ao espectro,
Pss( )
mathend000#, de s(t)
mathend000#. No caso realista de não dispormos de um conjunto infinito de observações independentes para calcular a média de conjunto, temos a complicada tarefa de dividir um intervalo infinito de observação num número infinito de sub-intervalos de duração infinita e calcular
)
mathend000#, de s(t)
mathend000#. No caso realista de não dispormos de um conjunto infinito de observações independentes para calcular a média de conjunto, temos a complicada tarefa de dividir um intervalo infinito de observação num número infinito de sub-intervalos de duração infinita e calcular
 ( ( ) = ) = 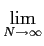 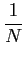 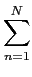 y(tn)y(tn - y(tn)y(tn -  ) (n - 1)T ) (n - 1)T tn tn nT. nT. |
(2-3.07) |
Obviamente, como não dispomos de um intervalo infinito, teremos de nos contentar com um número finito de intervalos, cada um deles finito, apenas com uma estimativa
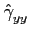 mathend000#, de
mathend000#, de
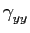 mathend000# para N
mathend000# finito. Assim um estimador de
mathend000# para N
mathend000# finito. Assim um estimador de
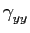 mathend000# poderá ser
mathend000# poderá ser
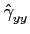 ( ( ) = ) = 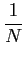 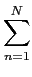 y(tn)y(tn - y(tn)y(tn -  ), (n - 1)T ), (n - 1)T tn tn nT nT |
(2-3.08) |
o que nos leva forçosamente a obter uma estimativa da densidade espectral
É essencialmente o facto de ter de estimar a função de correlação de um sinal aleatório num intervalo de observação finito que faz do cálculo da densidade espectral de potência um problema de estimação, denominado estimação espectral. A estimação espectral tem sido o tema de inúmeros trabalhos, investigações e descobertas nos últimos quarenta anos. Se as características estatísticas de determinado sinal pudessem ser conhecidas com exactidão a partir da observação de um intervalo finito desse sinal então a estimação espectral seria uma técnica determinística. Na realidade, só uma estimativa do espectro pode ser obtida a partir de uma única observação de um intervalo finito do sinal. A figura 2.3 ilustra a ambiguidade do problema da estimação espectral quando dois estimadores espectrais diferentes são usados no mesmo sinal resultando daí
mathend000#duas representações espectrais diferentes: qual delas é a verdadeira ? Não existe resposta para esta pergunta.
Figura 2.3:
densidade espectral de potência do mesmo sinal obtida através de um método de estimação espectral clássica (a) e um de alta resolução (b).
|
|
O facto de dispormos de sinais aleatórios em vez de determinísticos impõe uma análise estatística do sinal, i.e., temos de proceder a uma estimação da função de autocorrelação da sequência temporal fazendo para isso a hipótese de estacionaridade (e ergodicidade) resultando numa estimativa da DEP.
Densidade espectral de potência
A densidade espectral de potência (DEP ou PSD=power spectral density) é definida pela transformada de Fourier da função de autocorrelação de um processo estacionário, ou seja
Pxx(f )=  rxx( rxx( )e-j2 )e-j2 f f d d . . |
(2-3.10) |
Por outras palavras, a DEP descreve a distribuição da variância de um processo aleatório no domínio da frequência. Do mesmo modo, através da TF inversa,
rxx( ) = ) =  Pxx(f )ej2 Pxx(f )ej2 f f df. df. |
(2-3.11) |
Este par de transformadas de Fourier é chamado teorema de Wiener-Khintchine. Para  = 0
mathend000# temos que
= 0
mathend000# temos que
rxx(0) =  Pxx(f )df, Pxx(f )df, |
(2-3.12) |
o que significa que a autocorrelação para um desvio nulo é igual à potência total contida no espectro do sinal x(t)
mathend000#. Como para os sinais determinísticos, aplicam-se todas as propriedades da TF no que diz respeito, em particular, às simetrias de
rxx( )
mathend000# e de Pxx(f )
mathend000# para x(t)
mathend000# real.
)
mathend000# e de Pxx(f )
mathend000# para x(t)
mathend000# real.
Um processo aleatório particularmente interessante é o que representa o ruído branco contínuo w(t)
mathend000#, cuja função de autocorrelação é dada por
rww( ) =
) = 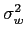
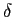 (
( )
mathend000#. A DEP do ruído branco escreve-se substituindo esta relação em (2-3.10), obtendo
)
mathend000#. A DEP do ruído branco escreve-se substituindo esta relação em (2-3.10), obtendo
| Pww(f ) |
= |
 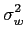 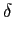 (t)e-j2 (t)e-j2 ftdt ftdt |
(2-3.13) |
| |
= |
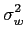 , , |
(2-3.14) |
que é constante qualquer que seja f
mathend000#. Podemos agora, a partir da resposta de um sistema linear invariante de resposta impulsiva h(t)
mathend000#, quando excitado por um sinal x(t)
mathend000#, dizer que a DEP do sinal resposta é obtida a partir da DEP do sinal excitação sabendo que para os sistemas lineares
y(t) = h(t) * x(t)  E[y(t)y(t - E[y(t)y(t -  )] = E[{h(t) * x(t)}{h(t - )] = E[{h(t) * x(t)}{h(t -  ) * x(t - ) * x(t -  )}]. )}]. |
(2-3.15) |
Aqui a notação da convolução é um pouco infeliz, pois na realidade não se deveria escrever
h(t) * x(t)
mathend000# mas sim
(h * x)(t)
mathend000#. Esta notação deficiente, traduz-se no facto de, no segundo termo da relação anterior, aparecer
h(t -  ) * x(t -
) * x(t -  )
mathend000# o que induz facilmente em erro. Utilizando uma notação explícita podemos escrever a partir de (2-3.15) que a função de autocorrelação de y(t)
mathend000# é dada por
)
mathend000# o que induz facilmente em erro. Utilizando uma notação explícita podemos escrever a partir de (2-3.15) que a função de autocorrelação de y(t)
mathend000# é dada por
ryy( ) ) |
= |
E[ h(u)x(t - u)du h(u)x(t - u)du h(v)x(t - h(v)x(t -  - v)dv] - v)dv] |
|
| |
= |
  h(u)h(v)E[x(t - u)x(t - h(u)h(v)E[x(t - u)x(t -  - v)]dudv, - v)]dudv, |
(2-3.16) |
fazendo uma mudança de variável apropriada
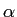 = t - u
mathend000# podemos escrever
= t - u
mathend000# podemos escrever
ryy( ) ) |
= |
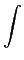 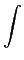 h(u)h(v)E[x( h(u)h(v)E[x(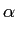 )x( )x(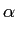 + - + -  - v)]dudv - v)]dudv |
|
| |
= |
  h(u)h(v)rxx( h(u)h(v)rxx( + v - u)dudv + v - u)dudv |
|
| |
= |
 h(v)[ h(v)[ h(u)rxx( h(u)rxx( + v - u)du]dv + v - u)du]dv |
|
| |
= |
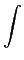 h(v)(h*rxx)( h(v)(h*rxx)( + v)dv + v)dv |
|
| |
= |
h( )*h(- )*h(-  )*rxx( )*rxx( ), ), |
(2-3.17) |
e finalmente fazendo a TF de ambos os membros da equação anterior
Pyy(f )= Pxx(f )|H(f ) . . |
(2-3.18) |
O caso interessante em muitas aplicações é quando o processo excitação é uma sequência de ruído branco e então
Pxx(f )= 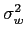 mathend000#.
mathend000#.
a título de exemplo vamos agora considerar um sinal sinusoidal discreto do tipo
x[n] = A sin(2 f0n + f0n +  ), ), |
(2-3.19) |
onde A
mathend000# é a amplitude, f0
mathend000# a frequência e 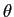 mathend000# a fase. A média estatística deste sinal é
mathend000# a fase. A média estatística deste sinal é
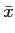 [n] = E[A sin(2 [n] = E[A sin(2 f0n + f0n +  )] = A sin(2 )] = A sin(2 f0n + f0n +  ), ), |
(2-3.20) |
que é uma função de n
mathend000# e portanto este sinal é não estacionário, i.e., a sua média de conjunto depende do instante onde é realizada. A autocorrelação do sinal x[n]
mathend000# escreve-se
| rxx[n + m, n] |
= |
E{x[n + m]x * [n]} |
|
| |
= |
E{A2sin(2 f0[n + m] + f0[n + m] +  )sin(2 )sin(2 f0n + f0n +  )} )} |
|
| |
= |
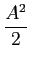 {cos(2 {cos(2 f0m) - cos[2 f0m) - cos[2 f0(2n + m) + 2 f0(2n + m) + 2 ]}, ]}, |
|
relação a partir da qual se torna óbvio que também a função de autocorrelação não é uma função do intervalo temporal entre os instantes considerados na correlação. A conclusão é que uma sinusoide determinística é não estacionária. No entanto se a fase for considerada como uma variável aleatória uniformemente distribuida em [0, 2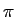 ]
mathend000# temos que
]
mathend000# temos que
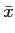 [n] [n] |
= |
E[A sin(2 f0n + f0n +  )] )] |
|
| |
= |
A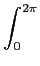 sin(2 sin(2 f0n + f0n +  ) )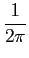 d d , , |
|
| |
= |
0 |
|
o que significa que na realidade
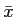 [n] =
[n] = 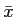 = 0
mathend000#, é independente de n
mathend000#. De notar que 1/2
= 0
mathend000#, é independente de n
mathend000#. De notar que 1/2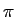 mathend000# na relação anterior é simplesmente a densidade de probabilidade da variável aleatória
mathend000# na relação anterior é simplesmente a densidade de probabilidade da variável aleatória 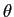 mathend000#. Da mesma forma
mathend000#. Da mesma forma
| rxx[n + m, n] |
= |
E{x[n + m]x * [n]} |
|
| |
= |
E{A2sin(2 f0[n + m] + f0[n + m] +  )sin(2 )sin(2 f0n + f0n +  )} )} |
|
| |
= |
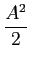 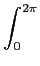 {cos(2 {cos(2 f0m) - cos[2 f0m) - cos[2 f0(2n + m) + 2 f0(2n + m) + 2 ]} ]}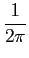 d d , , |
|
| |
= |
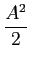 cos(2 cos(2 f0m), f0m), |
|
que é uma função apenas do intervalo m
mathend000# entre os instantes considerados, e portanto
rxx[n + m, n] = rxx[m] = (A2/2)cos(2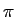 f0m)
mathend000#. Neste caso o sinal x[n]
mathend000# é estacionário (pelo menos no sentido lato).
f0m)
mathend000#. Neste caso o sinal x[n]
mathend000# é estacionário (pelo menos no sentido lato).
Por extensão, se o sinal for formado por uma soma de L
mathend000# sinusoides cujas fases são aleatórias, distribuidas uniformemente em [0, 2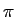 ]
mathend000# e independentes entre elas, tal que
]
mathend000# e independentes entre elas, tal que
x[n] = 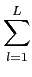 Alsin(2 Alsin(2 fln + fln + 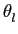 ) ) |
(2-3.21) |
então poderemos dizer que para a média
| E[x[n]] |
= |
E[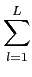 Alsin(2 Alsin(2 fln + fln + 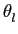 ), ), |
|
| |
= |
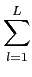 Al Al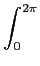 sin(2 sin(2 fln + fln + 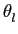 )p )p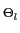 ( ( )d )d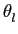 , , |
|
| |
= |
0, |
(2-3.22) |
porque os termos de fase são descorrelacionados entre si o que implica que a densidade de probabilidade conjunta se pode escrever como o produto das densidades de probabilidade
p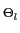 (
(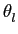 )
mathend000# para cada uma delas. Da mesma forma para a correlação,
)
mathend000# para cada uma delas. Da mesma forma para a correlação,
| rxx[n + m, n] |
= |
E{x[n + m]x * x[n]}, |
|
| |
= |
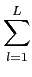 Al2 Al2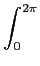 sin(2 sin(2 fl[n + m] + fl[n + m] + 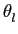 )sin(2 )sin(2 fln + fln + 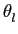 )p )p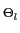 ( (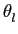 )d )d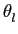 + + |
|
| |
|
+ 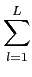 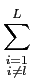 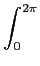 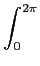 AlAisin(2 AlAisin(2 fl[n + m] + fl[n + m] +  ) ) |
|
| |
|
sin(2 fin + fin +  )p )p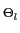 ( (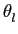 )p )p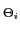 ( (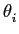 )d )d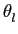 d d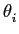 , , |
|
onde o segundo termo é nulo, permitindo assim dizer que
rxx[n + m, n] = rxx[m] = 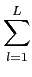 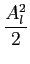 cos(2 cos(2 flm), flm), |
(2-3.23) |
e que o processo x[n]
mathend000# é também estacionário. Ainda, se as sinusoides forem complexas, i.e., se
x[n] = 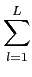 Alej(2 Alej(2 fln+ fln+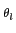 ), ), |
(2-3.24) |
então prova-se utilizando o mesmo raciocínio, que
rxx[m] = 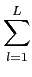 Al2ej2 Al2ej2 flm. flm. |
(2-3.25) |
Finalmente se adicionarmos ao sinal x[n]
mathend000# um ruído branco w[n]
mathend000# de média nula e variância
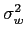 mathend000# e independente das fases das sinusoides, tal que
y[n] = x[n] + w[n]
mathend000#, então obtemos que
mathend000# e independente das fases das sinusoides, tal que
y[n] = x[n] + w[n]
mathend000#, então obtemos que
| ryy[m] |
= |
rxx[m] + rww[m] |
|
| |
= |
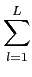 Al2ej2 Al2ej2 flm + flm + 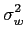 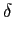 [m]. [m]. |
(2-3.26) |
Sinais aleatórios passa-banda
A adição de uma componente de ruído aleatório a um sinal passa-banda resulta num sinal passa-banda de natureza estocástica. Neste capítulo vamos generalizar as noções de sinais passa-banda e sua representação espectral ao caso de sinais estocásticos.
Consideremos um processo estocástico n(t)
mathend000# estacionário no sentido lato de média nula e de densidade espectral de potência Pnn(f )
mathend000#. À semelhança do caso dos sinais determinísticos, este processo aleatório será considerado de banda estreita se a sua densidade espectral de potência for aproximadamente zero fora de uma banda Bn
mathend000# tal que
Bn 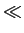 fc
mathend000#, onde fc
mathend000# é a frequência da portadora. Sob esta condição poderemos exprimir o processo passa-banda em função de grandezas equivalentes passa-baixo
fc
mathend000#, onde fc
mathend000# é a frequência da portadora. Sob esta condição poderemos exprimir o processo passa-banda em função de grandezas equivalentes passa-baixo
| n(t) |
= |
a(t)cos[2 fct + fct +  (t)], (t)], |
(2-3.27) |
| |
= |
x(t)cos 2 fct - y(t)sin 2 fct - y(t)sin 2 fct, fct, |
(2-3.28) |
| |
= |
Re[z(t)ej2 fct], fct], |
(2-3.29) |
onde z(t)
mathend000# é chamado envelope complexo ou componente em banda base de n(t)
mathend000#. Dada a relação que liga o processo estocástico passa-banda n(t)
mathend000# às suas componentes em quadratura x(t)
mathend000# e y(t)
mathend000# podemos deduzir que:
- tanto x(t)
mathend000# como y(t)
mathend000# são processos aleatórios de média nula, visto que E(n(t)] = 0
mathend000# e (2-3.29)
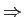 E[x(t)] = E[y(t)] = 0
mathend000#.
E[x(t)] = E[y(t)] = 0
mathend000#.
- a estacionaridade de n(t)
mathend000# implica que as funções de autocorrelação e correlação cruzada de x(t)
mathend000# e y(t)
mathend000# obedecem a
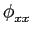 (
( ) =
) = 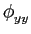 (
( )
mathend000# e que
)
mathend000# e que
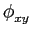 (
( ) = -
) = - 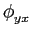 (
( )
mathend000#. Com efeito calculando a função de correlação do processo aleatório n(t)
mathend000#,
)
mathend000#. Com efeito calculando a função de correlação do processo aleatório n(t)
mathend000#,
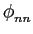 (t, t + (t, t +  ) ) |
= |
E[n(t), n * (t +  )] )] |
|
| |
= |
E[x(t)cos 2 fct - y(t)sin 2 fct - y(t)sin 2 fct] fct] |
|
| |
|
[x(t +  )cos 2 )cos 2 fc(t + fc(t +  ) - y(t + ) - y(t +  )sin 2 )sin 2 fc(t + fc(t +  )] )] |
|
| |
= |
E[x(t)x(t +  )] )] [cos 2 [cos 2 fc(2t + fc(2t +  ) + cos 2 ) + cos 2 fc fc ] - ] - |
|
| |
|
- E[y(t)xt +  )] )] [sin 2 [sin 2 fc(2t + fc(2t +  ) - sin 2 ) - sin 2 fc fc ] - ] - |
|
| |
|
- E[x(t)y(t +  )] )] [sin 2 [sin 2 fc(2t + fc(2t +  ) + sin 2 ) + sin 2 fc fc ] + ] + |
|
| |
|
+ E[y(t)y(t +  )] )] [cos 2 [cos 2 fc fc - cos 2 - cos 2 fc(2t + fc(2t +  )], )], |
|
de onde visto que n(t)
mathend000# é estacionário, os termos em t
mathend000# devem ser nulos, o que implica que
 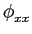 ( ( )cos 2 )cos 2 fc(2t + fc(2t +  ) ) |
- |
 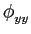 ( ( )cos 2 )cos 2 fc(2t + fc(2t +  ) = ) = |
|
| |
|
 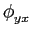 ( ( )sin 2 )sin 2 fc(2t + fc(2t +  ) + ) +  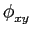 ( ( )sin 2 )sin 2 fc(2t + fc(2t +  ) ) |
|
ou seja, que para que esta última equação seja verificada, devemos ter que
- e também que
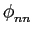 (
( ) =
) = 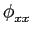 (
( )cos 2
)cos 2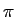 fc
fc -
- 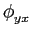 (
( )sin 2
)sin 2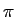 fc
fc mathend000#, consequência directa do ponto anterior, no caso n(t)
mathend000# estacionário.
mathend000#, consequência directa do ponto anterior, no caso n(t)
mathend000# estacionário.
- ainda que
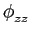 (
( ) =
) = 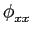 (
( ) + j
) + j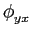 (
( )
mathend000#. Com efeito se utilizarmos a definição
)
mathend000#. Com efeito se utilizarmos a definição
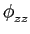 ( ( ) ) |
= |
E![$\displaystyle \left\{\vphantom{[x(t)+jy(t)][x(t+\tau)+jy(t+\tau)]^{\ast}}\right.$](img141.png) [x(t) + jy(t)][x(t + [x(t) + jy(t)][x(t +  ) + jy(t + ) + jy(t +  )] * )] * ![$\displaystyle \left.\vphantom{[x(t)+jy(t)][x(t+\tau)+jy(t+\tau)]^{\ast}}\right\}$](img142.png) |
|
| |
= |
E x(t)x * (t + x(t)x * (t +  ) + jy(t)x * (t + ) + jy(t)x * (t +  ) - jx(t)y * (t + ) - jx(t)y * (t +  ) + y(t)y * (t + ) + y(t)y * (t +  ) )![$\displaystyle \left.\vphantom{x(t)x^{\ast}(t+\tau) + jy(t)x^{\ast}(t+\tau) - jx(t)y^{\ast}(t+\tau) + y(t)y^{\ast}(t+\tau)}\right]$](img144.png) |
|
| |
= |
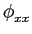 ( ( ) + j ) + j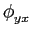 ( ( ) - j ) - j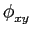 ( ( ) + ) + 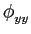 ( ( ) ) |
|
| |
= |
2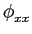 ( ( ) + 2j ) + 2j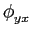 ( ( ), ), |
|
o que implica que
z(
t) =
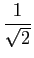
[
x(
t) +
jy(
t)].
mathend000#
- e finalmente que
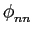 = Re[
= Re[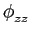 (
( )expj2
)expj2 fc
fc ]
mathend000#. Que se obtem a partir de (2-3.29),
]
mathend000#. Que se obtem a partir de (2-3.29),
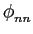 ( ( ) ) |
= |
E[n(t)n * (t +  )] )] |
|
| |
= |
E![$\displaystyle \left\{\vphantom{ {\rm Re}[z(t)e^{j2\pi f_c t}]{\rm Re}[z(t+\tau)e^{j2\pi f_c(t+\tau)}]}\right.$](img146.png) Re[z(t)ej2 Re[z(t)ej2 fct]Re[z(t + fct]Re[z(t +  )ej2 )ej2 fc(t+ fc(t+ )] )]![$\displaystyle \left.\vphantom{ {\rm Re}[z(t)e^{j2\pi f_c t}]{\rm Re}[z(t+\tau)e^{j2\pi f_c(t+\tau)}]}\right\}$](img147.png) |
|
| |
= |
 E[z(t)z(t + E[z(t)z(t +  )ej2 )ej2 fc(2t+ fc(2t+ ) + z * (t)z(t + ) + z * (t)z(t +  )ej2 )ej2 fc fc + + |
|
| |
|
+ z(t)z * (t +  )e-j2 )e-j2 fc fc + z * (t)z * (t + + z * (t)z * (t +  )e-j2 )e-j2 fc(2t+ fc(2t+ )], )], |
|
e dado que n(t)
mathend000# é estacionário temos que os termos dependentes de t
mathend000# deverão ser identicamente nulos o que implica necessariamente que
E[z(t)z(t +  )] )] |
= |
0 |
|
E[z * (t)z * (t +  )] )] |
= |
0, |
|
e finalmente
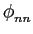 ( ( ) ) |
= |
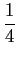  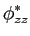 ( ( )ej2 )ej2 fc fc + + 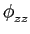 ( ( )e-j2 )e-j2 fc fc ![$\displaystyle \left.\vphantom{\phi_{zz}^{\ast}(\tau)e^{j2\pi f_c\tau} + \phi_{zz}(\tau)e^{-j2\pi f_c\tau}}\right]$](img150.png) |
|
| |
= |
 Re Re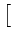 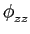 ( ( )ej2 )ej2 fc fc ![$\displaystyle \left.\vphantom{\phi_{zz}(\tau) e^{j2\pi f_c \tau}}\right]$](img152.png) . . |
|
Esta última relação implica que a autocorrelação do processo estocástico passa-banda pode ser definida de forma única a partir da função de autocorrelação da sua componente passa-baixo z(t)
mathend000# e da frequência da portadora fc
mathend000#. Assim podemos definir a densidade espectral de potência de n(t)
mathend000# como
| Pnn(f ) |
= |
 {Re[ {Re[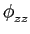 ( ( )ej2 )ej2 fc fc ]}e-j2 ]}e-j2 f f d d , , |
|
| |
= |
 [Pzz(f - fc) + Pzz * (- f - fc)]. [Pzz(f - fc) + Pzz * (- f - fc)]. |
(2-3.30) |
Como a função de autocorrelação
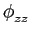 (
( )
mathend000# de z(t)
mathend000# é tal que
)
mathend000# de z(t)
mathend000# é tal que
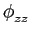 (
( ) =
) = 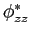 (-
(-  )
mathend000# então Pzz(f )
mathend000# é uma função real.
)
mathend000# então Pzz(f )
mathend000# é uma função real.
Ruído branco passa-banda
O problema subadjacente à caracterização do ruído branco passa-banda é de que, por definição, o ruído branco tem uma densidade espectral de potência que é de banda larga (teoricamente infinita) e constante para qualquer valor de f
mathend000# o que, obviamente, contraria a hipótese de banda estreita postulada no capítulo anterior. Portanto o termo ``ruído branco passa-banda'' não deveria teoricamente existir. No entanto, e na prática, chama-se ruído branco passa-banda, ao processo estocástico branco filtrado por um filtro passa-banda ideal de banda B
mathend000# em torno à frequência fc
mathend000# da portadora. Assim a densidade espectral do ruído branco pode-se escrever
Pww(f )= 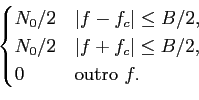 |
(2-3.31) |
Admitindo toda a notação introduzida no capítulo anterior para os processos aleatórios em geral, podemos definir o equivalente passa-baixo z(t)
mathend000# do ruído branco passa-banda w(t)
mathend000# cuja densidade espectral de potência se escreve então
Pzz(f )= 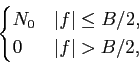 |
(2-3.32) |
e a sua função de autocorrelação escreve-se
tal que
De onde podemos deduzir que, tal como no caso do ruído branco em geral, tanto a densidade espectral de potência como a função de autocorrelação do ruído branco passa-banda são funções simétricas, o que implica, em particular,
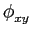 (
( ) = 0
mathend000# e que
) = 0
mathend000# e que
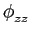 (
( ) =
) = 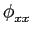 (
( ) =
) = 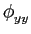 (
( )
mathend000#. Isto implica que tanto o sinal equivalente passa-baixo, como as componentes passa-baixo em fase e quadratura são descorrelacionadas e tem autocorrelações iguais para todos os atrasos
)
mathend000#. Isto implica que tanto o sinal equivalente passa-baixo, como as componentes passa-baixo em fase e quadratura são descorrelacionadas e tem autocorrelações iguais para todos os atrasos  mathend000#.
mathend000#.
Sinais cicloestacionários
Sinais cicloestacionários são sinais aleatórios cujas funções de autocorrelação são periódicas. Assim, a função de autocorrelação
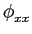 (t + (t +  , t) = E[x(t + , t) = E[x(t +  )x * (t)], )x * (t)], |
(2-4.01) |
é tal que
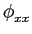 (t + (t +  + kT, t + kT) = + kT, t + kT) = 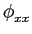 (t + (t +  , t), , t), |
(2-4.02) |
e portanto de período T
mathend000#. A caracterização destes sinais através da sua densidade espectral faz-se introduzindo a média temporal da sua função de autocorrelação num período que é
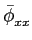 ( ( ) = ) = 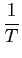 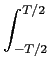 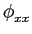 (t + (t +  , t)dt, , t)dt, |
(2-4.03) |
permitindo o cálculo da densidade espectral de potência média de um processo cicloestacionário definida por
Pxx(f )=  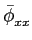 ( ( )e-j2 )e-j2 f f d d . . |
(2-4.04) |
Representação de sinais em expansões ortogonais
Para introduzir a expansão de sinais em bases ortogonais convém lembrar que, de forma análoga aos espaços vectoriais, nos quais podemos definir o produto vectorial e a norma, também para funções podemos escrever o produto interno entre duas funções definidas no intervalo [a, b]
mathend000# como sendo
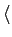 x1(t)x2(t) x1(t)x2(t)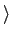 = = 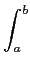 x1(t)x2 * (t)dt, x1(t)x2 * (t)dt, |
(2-5.01) |
no caso geral em que as funções podem ser complexas e onde *
mathend000# significa complexo conjugado. Como no caso dos vectores, se as funções forem ortogonais, temos que o seu produto interno é nulo. A partir da definição de produto interno é fácil chegar à noção de norma que é
| x(t)| = 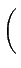 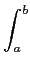 |x(t) |x(t) dt dt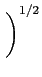 . . |
(2-5.02) |
Um conjunto de sinais é dito ortornormal se forem conjuntamente ortogonais e a sua norma for igual a um. Como no caso dos vectores um conjunto de sinais é dito linearmente independente, se nenhum deles pode ser representado como uma combinação linear dos outros. Adicionalmente, temos a desigualdade triangular que se escreve simplesmente
| x1(t) + x2(t)| 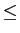 | x1(t)| + | x2(t)|, | x1(t)| + | x2(t)|, |
(2-5.03) |
e a desigualdade de Schwartz que se enuncia
|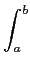 x1(t)x * 2(t)dt| x1(t)x * 2(t)dt|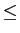 | |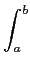 |x1(t) |x1(t) dt dt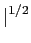 | |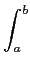 |x2(t) |x2(t) dt dt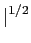 , , |
(2-5.04) |
na qual a igualdade é obtida se e só se
x1(t) = ax2(t)
mathend000#, onde a
mathend000# é uma constante complexa.
Vamos agora generalizar ao caso de um sinal s(t)
mathend000# real, determinístico e de energia finita
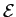 mathend000#,
mathend000#,
Podemos então aproximar o sinal s(t)
mathend000# como uma expansão 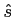 (t)
mathend000# numa determinada base de funções fn(t)
mathend000# como
(t)
mathend000# numa determinada base de funções fn(t)
mathend000# como
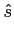 (t) = (t) = 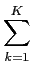 skfk(t) skfk(t) |
(2-5.06) |
onde a base de funções
{fk(t);k = 1,..., K}
mathend000# é ortonormal e onde
{sk;k = 1,..., K}
mathend000# são os coeficientes da expansão de s(t)
mathend000# na base que se encontram através da minimização da energia do erro quadrático
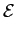 e e |
= |
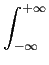 e2(t)dt, e2(t)dt, |
|
| |
= |
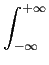 [s(t) - [s(t) - 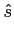 (t)]2dt. (t)]2dt. |
(2-5.07) |
A minimização de (2-5.7) pode ser efectuada de forma clássica diferenciando em relação a cada um dos coeficientes {sk}
mathend000# e anulando as derivadas ou, alternativamente, utilizando um resultado da teoria da estimação que consiste em considerar que o conjunto {sk}
mathend000# que minimiza a forma quadrática do erro corresponde ao caso em que a função de erro e(t)
mathend000#, é ortogonal a cada uma das funções da base
{fk(t)}
mathend000#. Uma explicação rápida desta noção consiste em observar que, devido às propriedades enunciadas acima, as funcções
{fk(t)}
mathend000# formam um sub-espaço vectorial (ou um plano) no qual se encontra também
![]() (t) + j/
(t) + j/![]() t
t
![]() (t)
(t)
![]() /2
/2
![]()
![$\displaystyle {c \ast \left[ {1\over {\pi t}} \right]}$](img53.png)
![]() ] = c
] = c![]() (f )[- jsgn(f )] = 0.
(f )[- jsgn(f )] = 0.![]() (t)]
(t)]![$\displaystyle {{\rm TH} \left[ x(t) \ast \left[ {1\over {\pi t}}\right]\right]}$](img55.png)
![$\displaystyle {x(t) \ast \left[ {1\over {\pi t}}\right] \ast \left[ {1\over {\pi t}}\right]}$](img56.png)
![]() (t)]]
(t)]]![]() (t)
(t)
![]() x(t)
x(t)![]() (t) * dt =
(t) * dt = ![]() X(f )
X(f )![]() (f ) * df
(f ) * df![]() x(t)
x(t)![]() (t) * dt
(t) * dt![]() X(f )[jsgn(f )X * (f )]df
X(f )[jsgn(f )X * (f )]df![]() X(f )X * (f )df+j
X(f )X * (f )df+j![]() X(f )X * (f )df
X(f )X * (f )df![]()
![]()
![]()
![]() (t) * h(t)
(t) * h(t)![]() (t).
(t).![]() t)
t)
![]() t)]]
t)]]![]() t)][- jsgn(f )]
t)][- jsgn(f )]![]() (f - fc)sgn(f )
(f - fc)sgn(f )![]() -jsgn(f )
-jsgn(f )![]() (f-fc)exp(j2
(f-fc)exp(j2![]() ft)df
ft)df![]() t).
t).![]() t +
t + ![]() )] = - jsgn(fc)exp(j
)] = - jsgn(fc)exp(j![]() t +
t + ![]() ).
).
![]() t +
t + ![]() )]
)]![]() t +
t + ![]() )
)![]() t +
t + ![]() )]
)]![]() t +
t + ![]() ).
).![]() t)
t)![]() t +
t + ![]() )] = - jsgn(fc)b(t)exp(j
)] = - jsgn(fc)b(t)exp(j![]() t +
t + ![]() ).
).![]() t]
t]![]() t
t![]() t]
t]![]() t
t![]() t +
t + ![]() (t)sin
(t)sin![]() t
t![]() (t)cos
(t)cos![]() t - x(t)sin
t - x(t)sin![]() t
t![]() |x(t)
|x(t)![]() dt =
dt = ![]() |
|![]() (t)
(t)![]() dt.
dt.![]() /2
/2
![]() (t)
(t)
![]() Re[sbb(t)ej2
Re[sbb(t)ej2![]() fct]e-j2
fct]e-j2![]() ftdt,
ftdt,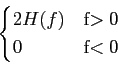 ,
,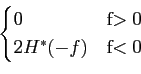 .
.![]() fc
fc
![]() 0
0
![]() [Sbb(f - fc)Hbb(f - fc) + Sbb * (- f - fc)Hbb * (- f - fc)],
[Sbb(f - fc)Hbb(f - fc) + Sbb * (- f - fc)Hbb * (- f - fc)],![]() [Rbb(f - fc) + Rbb * (- f - fc)],
[Rbb(f - fc) + Rbb * (- f - fc)],![]() s
s![]()
![]()
![]() [sbb(t)ej2
[sbb(t)ej2![]() fct + sbb * (t)e-j2
fct + sbb * (t)e-j2![]() fct]
fct]![]() dt
dt![]()
![]() {2sbb(t)sbb * (t) + sbb2(t)ej4
{2sbb(t)sbb * (t) + sbb2(t)ej4![]() fct + [sbb * (t)]2e-j4
fct + [sbb * (t)]2e-j4![]() fct}dt.
fct}dt.![]()
![]() (t)e-j
(t)e-j![]() (t)
(t)
![]() (t) =|sbb(t)|
(t) =|sbb(t)|
![]() =
= ![]() [sbb(t)]
[sbb(t)]
![]() s
s![]()
![]() |sbb(t)
|sbb(t)![]() dt +
dt + ![]()
![]()
![]() (t)[ej[4
(t)[ej[4![]() fct+2
fct+2![]() (t)] + e-j[4
(t)] + e-j[4![]() fct+2
fct+2![]() (t)]]dt,
(t)]]dt,![]()
![]() |sbb(t)
|sbb(t)![]() dt +
dt + ![]()
![]() |sbb(t)
|sbb(t)![]() cos[4
cos[4![]() fct + 2
fct + 2![]() (t)]dt,
(t)]dt,![]() , +
, + ![]() ]
]
![]() bb
bb
![]() t)
t)
![]()
![]() (
(![]() -
- ![]() ) +
) + ![]()
![]() (
(![]() +
+ ![]() )
)![]()
![]()
![]()
![]()
![]() ,
,![]() ]
]
![]() (
(![]() )
)
![]() (
(![]() ) =
) = ![]()
![]() (
(![]() )
)
![]() )
)
![]() (
(![]() ) =
) = ![]()
![]()
![]() y(tn)y(tn -
y(tn)y(tn - ![]() ) (n - 1)T
) (n - 1)T![]() tn
tn![]() nT.
nT.![]()
![]()
![]()
![]() (
(![]() ) = TF[
) = TF[![]() ].
].![\includegraphics[height=70mm,width=120mm]{figs/ambiguidade.ps}](img108.png)
![]() ) =
) = ![]() Pxx(f )ej2
Pxx(f )ej2![]() f
f![]() df.
df.![]() = 0
= 0
![]() )
)
![]() ) =
) = ![]()
![]() (
(![]() )
)
![]()
![]()
![]() (t)e-j2
(t)e-j2![]() ftdt
ftdt![]() ,
,![]() ) * x(t -
) * x(t - ![]() )
)
![]() = t - u
= t - u
![]() )
)![]()
![]() h(u)h(v)E[x(
h(u)h(v)E[x(![]() )x(
)x(![]() + -
+ - ![]() - v)]dudv
- v)]dudv![]()
![]() h(u)h(v)rxx(
h(u)h(v)rxx(![]() + v - u)dudv
+ v - u)dudv![]() h(v)[
h(v)[![]() h(u)rxx(
h(u)rxx(![]() + v - u)du]dv
+ v - u)du]dv![]() h(v)(h*rxx)(
h(v)(h*rxx)(![]() + v)dv
+ v)dv![]() )*h(-
)*h(- ![]() )*rxx(
)*rxx(![]() ),
),![]()
![]() f0n +
f0n + ![]() ),
),![]()
![]() [n] = E[A sin(2
[n] = E[A sin(2![]() f0n +
f0n + ![]() )] = A sin(2
)] = A sin(2![]() f0n +
f0n + ![]() ),
),![]() f0[n + m] +
f0[n + m] + ![]() )sin(2
)sin(2![]() f0n +
f0n + ![]() )}
)}![]() {cos(2
{cos(2![]() f0m) - cos[2
f0m) - cos[2![]() f0(2n + m) + 2
f0(2n + m) + 2![]() ]},
]},![]() ]
]
![]() [n]
[n]![]() f0n +
f0n + ![]() )]
)]![]() sin(2
sin(2![]() f0n +
f0n + ![]() )
)![]() d
d![]() ,
,![]() [n] =
[n] = ![]() = 0
= 0
![]()
![]()
![]() f0[n + m] +
f0[n + m] + ![]() )sin(2
)sin(2![]() f0n +
f0n + ![]() )}
)}![]()
![]() {cos(2
{cos(2![]() f0m) - cos[2
f0m) - cos[2![]() f0(2n + m) + 2
f0(2n + m) + 2![]() ]}
]}![]() d
d![]() ,
,![]() cos(2
cos(2![]() f0m),
f0m),![]() f0m)
f0m)
![]() ]
]
![]() Alsin(2
Alsin(2![]() fln +
fln + ![]() )
)![]() (
(![]() )
)
![]() Al2
Al2![]() sin(2
sin(2![]() fl[n + m] +
fl[n + m] + ![]() )sin(2
)sin(2![]() fln +
fln + ![]() )p
)p![]() (
(![]() )d
)d![]() +
+![]()
![]()
![]()
![]() AlAisin(2
AlAisin(2![]() fl[n + m] +
fl[n + m] + ![]() )
)![]() fin +
fin + ![]() )p
)p![]() (
(![]() )p
)p![]() (
(![]() )d
)d![]() d
d![]() ,
,![]()
![]() cos(2
cos(2![]() flm),
flm),![]() Alej(2
Alej(2![]() fln+
fln+![]() ),
),![]() Al2ej2
Al2ej2![]() flm.
flm.![]()
![]() Al2ej2
Al2ej2![]() flm +
flm + ![]()
![]() [m].
[m].![]() fc
fc
![]() fct +
fct + ![]() (t)],
(t)],![]() fct - y(t)sin 2
fct - y(t)sin 2![]() fct,
fct,![]() fct],
fct],![]() E[x(t)] = E[y(t)] = 0
E[x(t)] = E[y(t)] = 0
![]() (
(![]() ) =
) = ![]() (
(![]() )
)
![]() (
(![]() ) = -
) = - ![]() (
(![]() )
)
![]() (t, t +
(t, t + ![]() )
)![]() )]
)]![]() fct - y(t)sin 2
fct - y(t)sin 2![]() fct]
fct]![]() )cos 2
)cos 2![]() fc(t +
fc(t + ![]() ) - y(t +
) - y(t + ![]() )sin 2
)sin 2![]() fc(t +
fc(t + ![]() )]
)]![]() )]
)]![]() [cos 2
[cos 2![]() fc(2t +
fc(2t + ![]() ) + cos 2
) + cos 2![]() fc
fc![]() ] -
] -![]() )]
)]![]() [sin 2
[sin 2![]() fc(2t +
fc(2t + ![]() ) - sin 2
) - sin 2![]() fc
fc![]() ] -
] -![]() )]
)]![]() [sin 2
[sin 2![]() fc(2t +
fc(2t + ![]() ) + sin 2
) + sin 2![]() fc
fc![]() ] +
] +![]() )]
)]![]() [cos 2
[cos 2![]() fc
fc![]() - cos 2
- cos 2![]() fc(2t +
fc(2t + ![]() )],
)],![]()
![]() (
(![]() )cos 2
)cos 2![]() fc(2t +
fc(2t + ![]() )
)![]()
![]() (
(![]() )cos 2
)cos 2![]() fc(2t +
fc(2t + ![]() ) =
) =![]()
![]() (
(![]() )sin 2
)sin 2![]() fc(2t +
fc(2t + ![]() ) +
) + ![]()
![]() (
(![]() )sin 2
)sin 2![]() fc(2t +
fc(2t + ![]() )
)![]() (
(![]() )
)![]() (
(![]() )
)![]() (
(![]() )
)![]() (
(![]() )
)![]() (
(![]() ) =
) = ![]() (
(![]() )cos 2
)cos 2![]() fc
fc![]() -
- ![]() (
(![]() )sin 2
)sin 2![]() fc
fc![]()
![]() (
(![]() ) =
) = ![]() (
(![]() ) + j
) + j![]() (
(![]() )
)
![]() (
(![]() )
)![]() [x(t) + jy(t)][x(t +
[x(t) + jy(t)][x(t + ![]() ) + jy(t +
) + jy(t + ![]() )] *
)] * ![]()
![]() x(t)x * (t +
x(t)x * (t + ![]() ) + jy(t)x * (t +
) + jy(t)x * (t + ![]() ) - jx(t)y * (t +
) - jx(t)y * (t + ![]() ) + y(t)y * (t +
) + y(t)y * (t + ![]() )
)![]()
![]() (
(![]() ) + j
) + j![]() (
(![]() ) - j
) - j![]() (
(![]() ) +
) + ![]() (
(![]() )
)![]() (
(![]() ) + 2j
) + 2j![]() (
(![]() ),
),![]() [x(t) + jy(t)].
[x(t) + jy(t)].
![]() = Re[
= Re[![]() (
(![]() )expj2
)expj2![]() fc
fc![]() ]
]
![]() (
(![]() )
)![]() )]
)]![]() Re[z(t)ej2
Re[z(t)ej2![]() fct]Re[z(t +
fct]Re[z(t + ![]() )ej2
)ej2![]() fc(t+
fc(t+![]() )]
)]![]()
![]() E[z(t)z(t +
E[z(t)z(t + ![]() )ej2
)ej2![]() fc(2t+
fc(2t+![]() ) + z * (t)z(t +
) + z * (t)z(t + ![]() )ej2
)ej2![]() fc
fc![]() +
+![]() )e-j2
)e-j2![]() fc
fc![]() + z * (t)z * (t +
+ z * (t)z * (t + ![]() )e-j2
)e-j2![]() fc(2t+
fc(2t+![]() )],
)],![]() )]
)]![]() )]
)]![]() (
(![]() )
)![]()
![]()
![]() (
(![]() )ej2
)ej2![]() fc
fc![]() +
+ ![]() (
(![]() )e-j2
)e-j2![]() fc
fc![]()
![]()
![]() Re
Re![]()
![]() (
(![]() )ej2
)ej2![]() fc
fc![]()
![]() .
.![]() (
(![]() )
)
![]() (
(![]() ) =
) = ![]() (-
(- ![]() )
)
![]() (
(![]() ) = 0
) = 0
![]() (
(![]() ) =
) = ![]() (
(![]() ) =
) = ![]() (
(![]() )
)
![]()
![]()
![]() (t)
(t)
![]() (t)
(t)
![\includegraphics[width=10cm]{figs/fig2-2.eps}](img25.png)
![\includegraphics[width=14cm]{figs/fig2-3.eps}](img31.png)
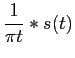 ,
,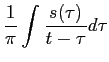 ,
,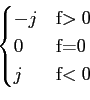 .
.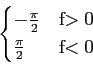 ,
, |sk
|sk
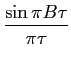 ,
,