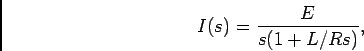Next: Circuito RLC
Up: Circuitos em regime transitório
Previous: Circuitos em regime transitório
Contents
Consideremos o circuito da figura 5.1. Neste circuito temos uma fonte de tensão de valor 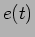 , variável, ligada em série com uma resistência
, variável, ligada em série com uma resistência 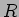 e um condensador
e um condensador 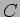 . A fonte de tensão varia como uma onda quadrada representada no gráfico da figura entre 0 e E volts. Estamos interessados em determinar como varia a tensão
. A fonte de tensão varia como uma onda quadrada representada no gráfico da figura entre 0 e E volts. Estamos interessados em determinar como varia a tensão 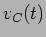 aos terminais do condensador
aos terminais do condensador 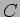 . Vamos começar por escrever a lei da malha
. Vamos começar por escrever a lei da malha
Figura 5.1:
circuito RC série (a) e forma de onda em 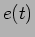 (b).
(b).
|
|
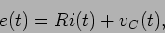 |
(5-1.01) |
por outro lado sabemos que
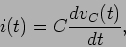 |
(5-1.02) |
substituindo (5-1.2) em (5-1.1) temos uma equação diferencial de primeira ordem com segundo membro em 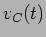 , que é
, que é
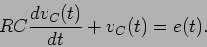 |
(5-1.03) |
Existem pelo menos duas formas de resolver a equação (5-1.3): uma é através da solução directa da equação diferencial considerando primeiro a equação homogénea e depois a equação forçada com segundo membro; a outra é utilizando a Transformada de Laplace (TL) estudada no capítulo anterior. Vamos utilizar a TL, calculando a TL de ambos os membros de (5-1.3) obtemos
![\begin{displaymath}
RC[sV_C(s) - v_C(0)] + V_C(s)=E(s),
\end{displaymath}](img584.png) |
(5-1.04) |
sabendo que o condensador se encontra descarregado no instante inicial, 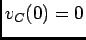 , temos que
, temos que
 |
(5-1.05) |
Basta-nos agora considerar o sinal 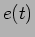 da figura 5.1(b) que se pode escrever como
da figura 5.1(b) que se pode escrever como
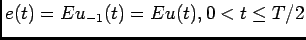 e por isso a sua TL nesse intervalo é dada por
e por isso a sua TL nesse intervalo é dada por
 |
(5-1.06) |
substituindo em (5-1.5) e decompondo em frações temos
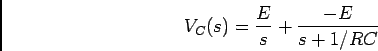 |
(5-1.07) |
de onde podemos tirar directamente a TLI
![\begin{displaymath}
v_C(t) = E[1-e^{-t/RC}]u(t)
\end{displaymath}](img590.png) |
(5-1.08) |
É claro que seria muito mais fácil utilizar directamente o cálculo simbólico, o nos permite não passar pela equação diferencial escrevendo imediatamente a partir do circuito da figura 5.1(a) o par de equações
onde considerámos logo que o condensador 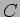 se encontrava descarregado no momento inicial, i.e., que
se encontrava descarregado no momento inicial, i.e., que 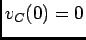 , e de onde tiramos logo (5-1.5).
, e de onde tiramos logo (5-1.5).
Figura 5.2:
descarga de um condensador.
|
|
Quando a tensão 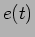 muda de
muda de 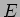 para 0 tudo se passa como no circuito equivalente da figura 5.2 onde o condensador se descarrega progressivamente na resistência
para 0 tudo se passa como no circuito equivalente da figura 5.2 onde o condensador se descarrega progressivamente na resistência 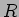 segundo uma equação idêntica a (5-1.3) com
segundo uma equação idêntica a (5-1.3) com 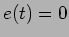 e portanto a solução deduz-se de (5-1.4) com
e portanto a solução deduz-se de (5-1.4) com 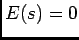 e
e
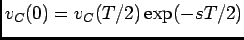 , o termo em exponencial significa apenas que tudo se passa em
, o termo em exponencial significa apenas que tudo se passa em 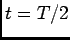 em vez de em
em vez de em  (ver discussão em torno ao cálculo de
(ver discussão em torno ao cálculo de 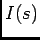 na equação (d) do exemplo 1 de 4.5). Assim
na equação (d) do exemplo 1 de 4.5). Assim
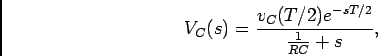 |
(5-1.11) |
e portanto calculando a TLI
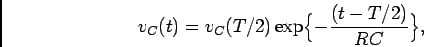 |
(5-1.12) |
e a forma completa de 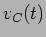 está representada na curva (a) da figura 5.3 para
está representada na curva (a) da figura 5.3 para 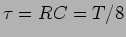 .
.
Figura 5.3:
tensão aos bornos de um condensador (a) e corrente de carga (b).
|
|
Calculando a derivada da função 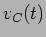 de (5-1.8) obtem-se
de (5-1.8) obtem-se
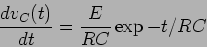 |
(5-1.13) |
de onde se deduz o coeficiente director na origem fazendo  ,
,
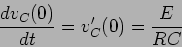 |
(5-1.14) |
e por isso a equação da recta tangente à curva 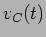 na origem escreve-se
na origem escreve-se
 |
(5-1.15) |
quando esta recta atinge o valor final da curva 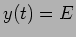 temos que
temos que 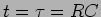 conforme representado na figura 5.3. Se o valor de
conforme representado na figura 5.3. Se o valor de 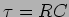 , que é chamada constante de tempo do circuito, fosse muito inferior a
, que é chamada constante de tempo do circuito, fosse muito inferior a 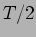 então a carga seria muito rápida e ao limite
então a carga seria muito rápida e ao limite 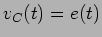 . Se
. Se 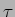 fosse muito superior a
fosse muito superior a 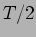 , então o sinal de saída não iria atingir o seu valor final no intervalo
, então o sinal de saída não iria atingir o seu valor final no intervalo 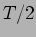 considerado e
considerado e 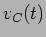 iria ser, ao limite, desprezável em relação a
iria ser, ao limite, desprezável em relação a 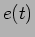 .
.
A corrente 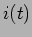 no circuito é dada por (5-1.2) onde
no circuito é dada por (5-1.2) onde 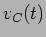 tem a forma (5-1.8) para
tem a forma (5-1.8) para 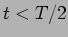 e então
e então
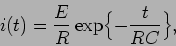 |
(5-1.16) |
para 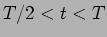 temos que
temos que
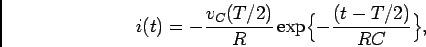 |
(5-1.17) |
e cujo gráfico está representado na figura 5.3(b).
Em termos energéticos, utilizando a equação (2-4.7), podemos dizer que a energia armazenada no condensador quando carregado à tensão 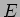 , é
, é
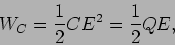 |
(5-1.18) |
por outro lado a energia fornecida pela fonte é 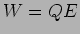 , concluindo-se que só metade da energia fornecida pela fonte é armazenada pelo condensador, sendo a outra metade dissipada na resistência
, concluindo-se que só metade da energia fornecida pela fonte é armazenada pelo condensador, sendo a outra metade dissipada na resistência 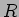 .
.
Exemplo: consideremos o circuito da figura 5.4.
Figura 5.4:
circuito RL série.
|
|
Neste circuito está representada uma fonte de tensão alternada semelhante à da figura 5.1 e com a mesma onda quadrada à entrada. A fonte de tensão encontra-se em série com uma resistência 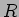 e uma bobine
e uma bobine 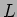 . Pretendemos determinar a corrente
. Pretendemos determinar a corrente 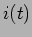 atravessando a bobine e a tensão aos seus bornos
atravessando a bobine e a tensão aos seus bornos 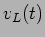 .
.
Podemos começar por escrever a equação que rege o circuito,
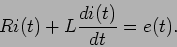 |
(5-1.19) |
Resolvendo como no caso RC através da TL, obtemos
![\begin{displaymath}
R I(s) + L[sI(s)+i(0)]=E(s),
\end{displaymath}](img621.png) |
(5-1.20) |
com 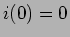 e
e 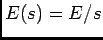 chegamos a um resultado idêntico aquele encontrado no caso do circuito RC, i.e., que a corrente
chegamos a um resultado idêntico aquele encontrado no caso do circuito RC, i.e., que a corrente 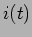 no circuito se pode exprimir como a soma de dois termos: um devido ao degrau unidade à entrada e outro que é uma exponencial amortecida com uma constante de tempo dependente dos valores dos elementos do circuito, neste caso a resistência
no circuito se pode exprimir como a soma de dois termos: um devido ao degrau unidade à entrada e outro que é uma exponencial amortecida com uma constante de tempo dependente dos valores dos elementos do circuito, neste caso a resistência 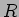 e a bobine
e a bobine 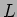 . Assim
. Assim
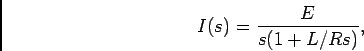 |
(5-1.21) |
e portanto
![\begin{displaymath}
i(t) = {E\over R}\Bigl[ 1-\exp\Bigl\{-{R\over L}t\Bigr\}\Bigr].
\end{displaymath}](img625.png) |
(5-1.22) |
Figura 5.5:
corrente (a) e tensão (b) num circuito RL série.
|
|
A tensão 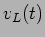 é obtida facilmente através da derivação de (5-1.22) segundo (5-1.23). A figura 5.5 mostra os gráficos da tensão e corrente no circuito em função do tempo para o sinal de entrada
é obtida facilmente através da derivação de (5-1.22) segundo (5-1.23). A figura 5.5 mostra os gráficos da tensão e corrente no circuito em função do tempo para o sinal de entrada 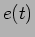 . Podemos fazer o mesmo raciocínio acerca dos valores relativos entre
. Podemos fazer o mesmo raciocínio acerca dos valores relativos entre 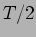 e a constante de tempo do circuito que é neste caso
e a constante de tempo do circuito que é neste caso 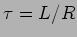 .
.
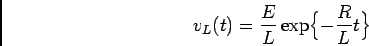 |
(5-1.23) |




Next: Circuito RLC
Up: Circuitos em regime transitório
Previous: Circuitos em regime transitório
Contents
Sergio Jesus
2003-12-07
![]() , variável, ligada em série com uma resistência
, variável, ligada em série com uma resistência ![]() e um condensador
e um condensador ![]() . A fonte de tensão varia como uma onda quadrada representada no gráfico da figura entre 0 e E volts. Estamos interessados em determinar como varia a tensão
. A fonte de tensão varia como uma onda quadrada representada no gráfico da figura entre 0 e E volts. Estamos interessados em determinar como varia a tensão ![]() aos terminais do condensador
aos terminais do condensador ![]() . Vamos começar por escrever a lei da malha
. Vamos começar por escrever a lei da malha
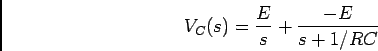
![]() muda de
muda de ![]() para 0 tudo se passa como no circuito equivalente da figura 5.2 onde o condensador se descarrega progressivamente na resistência
para 0 tudo se passa como no circuito equivalente da figura 5.2 onde o condensador se descarrega progressivamente na resistência ![]() segundo uma equação idêntica a (5-1.3) com
segundo uma equação idêntica a (5-1.3) com ![]() e portanto a solução deduz-se de (5-1.4) com
e portanto a solução deduz-se de (5-1.4) com ![]() e
e
![]() , o termo em exponencial significa apenas que tudo se passa em
, o termo em exponencial significa apenas que tudo se passa em ![]() em vez de em
em vez de em ![]() (ver discussão em torno ao cálculo de
(ver discussão em torno ao cálculo de ![]() na equação (d) do exemplo 1 de 4.5). Assim
na equação (d) do exemplo 1 de 4.5). Assim
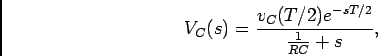
![]() no circuito é dada por (5-1.2) onde
no circuito é dada por (5-1.2) onde ![]() tem a forma (5-1.8) para
tem a forma (5-1.8) para ![]() e então
e então
![]() , é
, é
![]() e uma bobine
e uma bobine ![]() . Pretendemos determinar a corrente
. Pretendemos determinar a corrente ![]() atravessando a bobine e a tensão aos seus bornos
atravessando a bobine e a tensão aos seus bornos ![]() .
.