Exemplo 1: utilizando o cálculo simbólico da TL, queremos saber qual a evolução da tensão ![]() aos terminais do condensador da figura 4.9 sabendo que no instante
aos terminais do condensador da figura 4.9 sabendo que no instante ![]() temos
temos ![]() V. O interruptor S fecha-se para
V. O interruptor S fecha-se para ![]() , abre para
, abre para ![]() ms e fecha novamente para
ms e fecha novamente para ![]() ms até 3 ms. Determine as expressões de
ms até 3 ms. Determine as expressões de ![]() e as formas de onda para
e as formas de onda para ![]() ms.
ms.
Para ![]() ms, com o interruptor S fechado podemos escrever
ms, com o interruptor S fechado podemos escrever
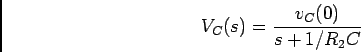
Para
![]() ms, o condensador
ms, o condensador ![]() encontra-se em série com as duas resistências
encontra-se em série com as duas resistências ![]() e
e ![]() de 100 k
de 100 k![]() cada. Nesse caso o novo sistema de equações em Laplace é
cada. Nesse caso o novo sistema de equações em Laplace é
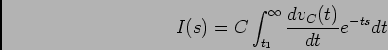
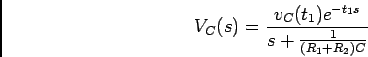
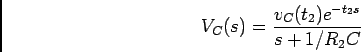
A forma de onda de ![]() é formada por arcos de exponencial decrescente com
é formada por arcos de exponencial decrescente com ![]() v,
v, ![]() v e
v e ![]() v.
v.
Exemplo 2: a figura 4.10 representa um cicuito contendo apenas uma bobine e um condensador (L=1/![]() H, C=25
H, C=25 ![]() F). Antes do interruptor S se fechar temos
F). Antes do interruptor S se fechar temos ![]() V. Utilizando o cálculo simbólico da TL, determine:
V. Utilizando o cálculo simbólico da TL, determine:
a) a evolução da corrente ![]() no circuito.
no circuito.
b) a evolução da tensão ![]() .
.
a) Com o interruptor S fechado escrevemos
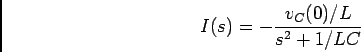
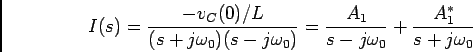

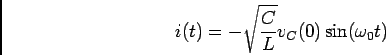
b) agora podíamos resolver o sistema em relação a ![]() mas é bastante mais simples escrever
mas é bastante mais simples escrever