



Next: Elementos ideais activos
Up: Elementos de circuitos
Previous: Elementos de circuitos
Contents
A resistência: uma resistência 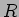 dá origem a um potencial
dá origem a um potencial 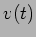 quando percorrida por uma corrente
quando percorrida por uma corrente 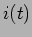 (figura 2.5a), é
(figura 2.5a), é
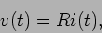 |
(2-4.01) |
e inversamente
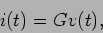 |
(2-4.02) |
onde 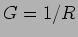 é uma conductância e se exprime em
é uma conductância e se exprime em 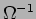 . A resistência equivalente a duas resistências
. A resistência equivalente a duas resistências 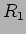 e
e 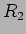 colocadas em série, i.e., tal que a corrente que percorre uma é igual à corrente que percorre a outra é
colocadas em série, i.e., tal que a corrente que percorre uma é igual à corrente que percorre a outra é
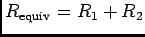 . Se as resistências se encontrarem em paralelo, i.e., se a tensão aos terminais duma for igual à tensão aos terminais da outra, então a resistência equivalente é evidentemente,
. Se as resistências se encontrarem em paralelo, i.e., se a tensão aos terminais duma for igual à tensão aos terminais da outra, então a resistência equivalente é evidentemente,
 |
(2-4.03) |
A título de exercício determine a resistência equivalente a três resistências colocadas em série e em paralelo. E se em vez de resistências tivermos conductâncias ? Qual será a conductância equivalente a duas ou três conductâncias em série e/ou em paralelo ?
Como já foi dito acima, a quantidade instantânea de energia posta em jogo numa resistência é sempre positiva, i.e., uma resistência absorve sempre a energia
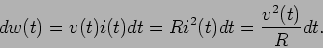 |
(2-4.04) |
Figura 2.5:
dipólo resistivo (a), dipólo capacitivo (b)
e dipólo inductivo(c).
|
|
O condensador: um condensador 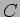 armazena energia sob forma de campo eléctrico entre as suas armaduras. Assim, com as definições da figura 2.5b, temos que
armazena energia sob forma de campo eléctrico entre as suas armaduras. Assim, com as definições da figura 2.5b, temos que
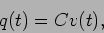 |
(2-4.05) |
e que
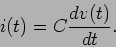 |
(2-4.06) |
A variação da energia contida num condensador escreve-se
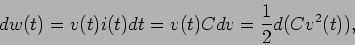 |
(2-4.07) |
o que mostra que a energia depende de forma estreita da variação da tensão aos seus terminais: positiva se esta for positiva e
negativa no caso contrário. Isto significa que um condensador absorve energia, armazena-a sob forma electrostática, e pode restitui-la mais tarde. Mais uma vez qual o valor do condensador equivalente a dois condensadores colocados em série ? E em paralelo ?
Bobine(self): uma bobine, de inductância 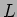 , armazena energia sob forma de campo magnético. Uma bobine tem como princípio o de se opôr à variação da corrente. Esta corrente cria à sua passagem um fluxo de inducção magnética
, armazena energia sob forma de campo magnético. Uma bobine tem como princípio o de se opôr à variação da corrente. Esta corrente cria à sua passagem um fluxo de inducção magnética
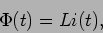 |
(2-4.08) |
que se opõe (pela regra dos três dedos) à causa que o criou (ou seja à corrente). Podemos ainda escrever (figura 2.5c)
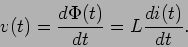 |
(2-4.09) |
No caso da bobine a relação energética escreve-se
![\begin{displaymath}
dw(t) = v(t) i(t) dt = L i(t) di = {1\over 2} d[L i^2(t)],
\end{displaymath}](img124.png) |
(2-4.10) |
que, como no caso do condensador, mostra que a energia pode tomar valores positivos ou negativos consoante a variação, neste caso da corrente eléctrica, que percorre a bobine. As relações energéticas instantâneas (2-4.7) e (2-4.10) permitem-nos calcular o valor total da energia armazenado num condensador e bobine respectivamente, permite-nos calcular
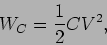 |
(2-4.11) |
e
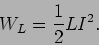 |
(2-4.12) |
Exemplo: no circuito da figura 2.6(a), 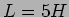 e
e  . Calcular
. Calcular 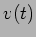 quando
quando 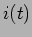 tem a forma indicada no gráfico da figura 2.6(b).
tem a forma indicada no gráfico da figura 2.6(b).
Figura 2.6:
(a) circuito RL e (b) corrente 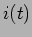 .
.
|
|
Comecemos por escrever a equação de Ohm no dipólo da figura 2.6(a). Assim temos que a queda de tensão é a soma das tensões aos terminais dos elementos do circuito, i.e.,
e escrevendo a mesma relação para cada elemento
sabendo que 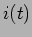 se escreve a partir da figura 2.6(b) como
se escreve a partir da figura 2.6(b) como
e que depois se repete com um período igual a 6, podemos então escrever (utilizando os valores numéricos)
dando lugar à representação gráfica da figura 2.7
Figura 2.7:
tensão aos terminais do circuito da figura 2.6.
|
|




Next: Elementos ideais activos
Up: Elementos de circuitos
Previous: Elementos de circuitos
Contents
Sergio Jesus
2003-12-07
![]() dá origem a um potencial
dá origem a um potencial ![]() quando percorrida por uma corrente
quando percorrida por uma corrente ![]() (figura 2.5a), é
(figura 2.5a), é

![]() armazena energia sob forma de campo eléctrico entre as suas armaduras. Assim, com as definições da figura 2.5b, temos que
armazena energia sob forma de campo eléctrico entre as suas armaduras. Assim, com as definições da figura 2.5b, temos que
![]() , armazena energia sob forma de campo magnético. Uma bobine tem como princípio o de se opôr à variação da corrente. Esta corrente cria à sua passagem um fluxo de inducção magnética
, armazena energia sob forma de campo magnético. Uma bobine tem como princípio o de se opôr à variação da corrente. Esta corrente cria à sua passagem um fluxo de inducção magnética
![]() e
e ![]() . Calcular
. Calcular ![]() quando
quando ![]() tem a forma indicada no gráfico da figura 2.6(b).
tem a forma indicada no gráfico da figura 2.6(b).