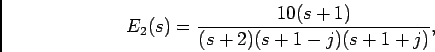Next: Caracterização de circuitos em
Up: Circuitos em regime transitório
Previous: Circuitos RC
Contents
Na figura 5.6 colocámos em série uma fonte de tensão e três elementos: uma resistência 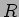 , uma bobine
, uma bobine 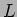 e um condensador
e um condensador 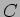 .
.
Figura 5.6:
circuito RLC série.
|
|
A lei das malhas permite-nos escrever,
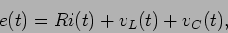 |
(5-2.01) |
substituindo as expressões de 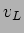 e
e 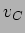 obtemos
obtemos
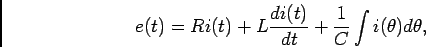 |
(5-2.02) |
Utilizando directamente a representação simbólica para cada elemento do circuito e que 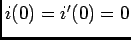 , podemos escrever
, podemos escrever
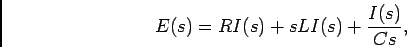 |
(5-2.03) |
e portanto, arranjando um pouco a equação em ordem a 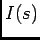 e definindo as seguintes constantes
e definindo as seguintes constantes 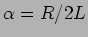 e
e
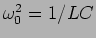 , obtem-se facilmente
, obtem-se facilmente
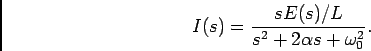 |
(5-2.04) |
Obviamente que a expressão da corrente 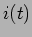 resultante da TLI de
resultante da TLI de 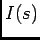 , vai ser completamente determinada pelas raízes da equação do segundo grau que forma o denominador de (5-2.4) - frequentemente denominada ``equação característica''. Estas raízes são
, vai ser completamente determinada pelas raízes da equação do segundo grau que forma o denominador de (5-2.4) - frequentemente denominada ``equação característica''. Estas raízes são
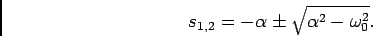 |
(5-2.05) |
Os casos possíveis segundo os valores relativos de 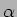 e
e 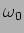 estão resumidos na tabela 1 que acompanha a figura 5.7, na qual estão representadas as raízes no plano complexo.
estão resumidos na tabela 1 que acompanha a figura 5.7, na qual estão representadas as raízes no plano complexo.
A decomposição em factores de (5-2.4) permite obter
 |
(5-2.06) |
com
Assim, podemos escrever a
![${\rm TLI}[I(s)]$](img642.png) ,
,
![\begin{displaymath}
i(t) = {{E e^{-\alpha t}}\over {2L\sqrt{\alpha^2-\omega_0^2}...
...rt{\alpha^2-\omega_0^2}t} - e^{-\sqrt{\alpha^2-\omega_0^2}t}].
\end{displaymath}](img643.png) |
(5-2.07) |
Tabela 1:
características dos quatro regimes de funcionamento
possíveis dos circuitos de segunda ordem.
| |
regime |
|
raízes |
sinal de saída |
| 1 |
não |
 |
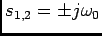 |
onda sinusoidal |
| |
amortecido |
|
|
|
| 2 |
sobre |
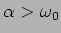 |
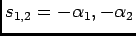 |
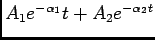 |
| |
amortecido |
|
|
|
| 3 |
crítico |
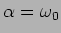 |
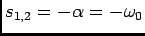 |
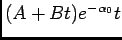 |
| 4 |
sub |
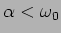 |
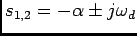 |
seno
amortecido |
| |
amortecido |
|
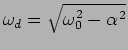 |
|
|
Figura 5.7:
raízes do sistema de segundo grau no plano complexo.
|
|
Vamos agora estudar cada uma das quatro situações possíveis segundo os valores relativos de 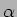 e
e 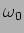 .
.
a) Caso 1: regime não amortecido
Neste caso temos que  e portanto as raízes são imaginárias puras
e portanto as raízes são imaginárias puras
 |
(5-2.08) |
e a resposta é então
ou ainda
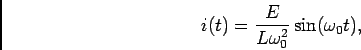 |
(5-2.09) |
e temos portanto um regime sinusoidal puro à frequência
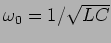 .
.
b) Caso 2: regime sobre amortecido
Neste caso temos que
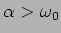 e portanto as raízes são reais
e portanto as raízes são reais
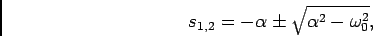 |
(5-2.10) |
e a resposta é então
![\begin{displaymath}
i(t) = {{E e^{-\alpha t}}\over {2L\sqrt{\alpha^2-\omega_0^2}...
...rt{\alpha^2-\omega_0^2}t} - e^{-\sqrt{\alpha^2-\omega_0^2}t}].
\end{displaymath}](img643.png) |
(5-2.11) |
de notar que ambas as raízes além de reais são negativas o que forma uma resposta exponencial amortecida.
c) Caso 3: regime crítico
Neste caso temos que
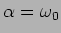 , correspondente ao caso
, correspondente ao caso
valor crítico da resistência, e portanto temos uma raíz dupla
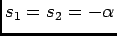 . Se nos limitarmos a efectuar esta substituição em (5-2.7) obtemos uma indeterminação. Deveremos então utilizar o desenvolvimento em série da exponencial em torno a zero para encontrar
. Se nos limitarmos a efectuar esta substituição em (5-2.7) obtemos uma indeterminação. Deveremos então utilizar o desenvolvimento em série da exponencial em torno a zero para encontrar
e ainda
 |
(5-2.12) |
d) Caso 4: regime sub amortecido
Neste caso temos que
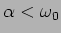 e portanto as raízes são complexas conjugadas e imaginárias puras
e portanto as raízes são complexas conjugadas e imaginárias puras
assim
 |
(5-2.13) |
onde
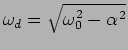 e a resposta é então do tipo
e a resposta é então do tipo
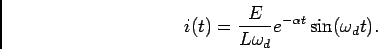 |
(5-2.14) |
dando origem a uma sinusoide com pulsação 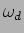 que se amortece exponencialmente com o coeficiente de amortecimento
que se amortece exponencialmente com o coeficiente de amortecimento 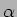 .
.
Exemplo: considerando o circuito de segunda ordem da figura 5.8 com
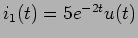 , pretendemos calcular a tensão
, pretendemos calcular a tensão 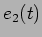 aos bornos da bobine e da resistência em série considerando condições iniciais nulas.
aos bornos da bobine e da resistência em série considerando condições iniciais nulas.
Figura 5.8:
circuito de segunda ordem.
|
|
Começando por estabelecer o sistema de equações diferenciais, obtem-se
e a corrente na bobine
por substituição e reagrupando os termos em 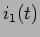 e
e 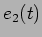 temos
temos
cuja TL é dada por
visto que
![$I_1(s) = {\rm TL}[i_1(t)]$](img677.png) é dada por
é dada por
temos que, por substituição na equação anterior, e cálculo das raízes da equação do segundo grau do denominador
dando origem à representação no plano 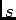 da figura 5.9 e finalmente à TLI (caso idêntico ao exemplo do capítulo 4.2)
da figura 5.9 e finalmente à TLI (caso idêntico ao exemplo do capítulo 4.2)
![\begin{displaymath}
e_2(t) = [5\sqrt{2} e^{-t} \cos(t-{{\pi}\over 4}) - 5e^{-2t}]u(t).
\end{displaymath}](img680.png) |
(5-2.15) |
Figura 5.9:
pólos e zeros no plano 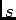 .
.
|
|
Retomemos o exemplo do circuito de segunda ordem da figura 5.8, utilizando agora o cálculo simbólico directamente.
Podemos então escrever directamente a admitância
e, visto que
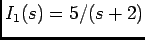 , temos que
, temos que
equação idêntica à anterior mas que se obteve apenas em dois passos. Na resposta (5-2.15) podemos distinguir perfeitamente que o primeiro termo é devido à resposta natural do sistema e o segundo termo é devido únicamente à excitação 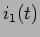 .
.




Next: Caracterização de circuitos em
Up: Circuitos em regime transitório
Previous: Circuitos RC
Contents
Sergio Jesus
2003-12-07
![]() , uma bobine
, uma bobine ![]() e um condensador
e um condensador ![]() .
.


![]() e
e ![]() .
.
![]() e portanto as raízes são imaginárias puras
e portanto as raízes são imaginárias puras
![\begin{displaymath}i(t) = {E\over {2Lj\omega_0^2}}[e^{j\omega_0 t} - e^{-j\omega_0 t}]\end{displaymath}](img657.png)
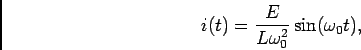
![]() e portanto as raízes são reais
e portanto as raízes são reais
![\begin{displaymath}
i(t) = {{E e^{-\alpha t}}\over {2L\sqrt{\alpha^2-\omega_0^2}...
...rt{\alpha^2-\omega_0^2}t} - e^{-\sqrt{\alpha^2-\omega_0^2}t}].
\end{displaymath}](img643.png)
![]() , correspondente ao caso
, correspondente ao caso

![\begin{displaymath}i(t) \approx {E\over {2L\sqrt{\alpha^2-\omega_0^2}}}e^{-\alph...
...1+\sqrt{\alpha^2-\omega_0^2}t - 1+\sqrt{\alpha^2-\omega_0^2}t],\end{displaymath}](img663.png)
![]() e portanto as raízes são complexas conjugadas e imaginárias puras
e portanto as raízes são complexas conjugadas e imaginárias puras
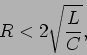
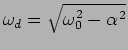 e a resposta é então do tipo
e a resposta é então do tipo
![]() , pretendemos calcular a tensão
, pretendemos calcular a tensão ![]() aos bornos da bobine e da resistência em série considerando condições iniciais nulas.
aos bornos da bobine e da resistência em série considerando condições iniciais nulas.