Subsecções
Transformada de Laplace
A utilidade da Transformada de Laplace (TL) decorre da necessidade de representar funções temporais no domínio da frequência complexa ou plano complexo, no qual a variável, geralmente designada pela letra s
mathend000# ou p
mathend000#, é uma variável complexa
p = 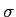 + j
+ j mathend000#1. Devido à utilidade da TL na manipulação de funções de variável complexa, tornou-se um utensílio essencial na análise e na síntese de sistemas lineares.
mathend000#1. Devido à utilidade da TL na manipulação de funções de variável complexa, tornou-se um utensílio essencial na análise e na síntese de sistemas lineares.
Definição e existência
Começaremos pela sua definição no caso geral, que vem essencialmente da definição de Transformada de Fourier (TF), e que é
F(s) =  f (t)e-stdt, f (t)e-stdt,
|
(3-1.01) |
mathend000#
que é denominada Transformada de Laplace (TL) bilateral, devido ao domínio de integração se estender de - 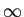 mathend000# a +
mathend000# a + 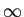 mathend000#. Devido ao facto de, na prática, nos interessarmos quase exclusivamente pelas funções causais que são nulas para t
mathend000#. Devido ao facto de, na prática, nos interessarmos quase exclusivamente pelas funções causais que são nulas para t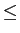 0
mathend000#, seremos levados a utilizar mais frequentemente a TL unilateral que se escreve
0
mathend000#, seremos levados a utilizar mais frequentemente a TL unilateral que se escreve
F(s) = 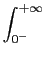 f (t)e-stdt, f (t)e-stdt,
|
(3-1.02) |
mathend000#
na qual devemos no entanto precisar que o limite inferior inclui o ponto de origem do eixo do tempo; em particular, um impulso de Dirac na origem deverá ser tido em conta na TL. A transformada inversa é obtida, sempre através da analogia com a TF, por
f (t) = 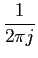 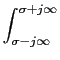 F(s)estds, F(s)estds,
|
(3-1.03) |
mathend000#
onde, neste caso, o integral é de variável complexa.
Uma das questões mais importante no cálculo da TL é, antes de mais, a da sua existência. Já sabemos, a partir da TF, que a TL existe quando o integral de definição converge no intervalo considerado. Em geral utiliza-se a noção de convergência no sentido absoluto, i.e., que
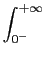 |x(t)|dt < |x(t)|dt < 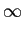 , ,
|
(3-1.04) |
mathend000#
que é uma noção mais exigente do que, se em vez de
|x(t)|
mathend000#, utilizarmos apenas x(t)
mathend000#. Devido ao facto de que, em teoria de sinais, a maior parte das funções são de tipo exponencial para as quais
|
x(
t)|<
eCt quando t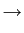
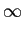
,
mathend000#
onde C
mathend000# é uma constante real, coloca-se a questão de convergência para este tipo de funções, para as quais é importante relembrar a noção de abcissa de convergência absoluta. Podemos escrever (3-1.2) como
F(s) = 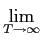 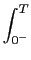 f (t)e-stdt, f (t)e-stdt,
|
(3-1.05) |
mathend000#
podendo demonstrar-se que se a função f (t)
mathend000# for de tipo exponencial (3-1.5) converge sempre, i.e., a sua TL existe. Além disso podemos também dizer em geral que
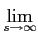 F(s) = 0. F(s) = 0.
|
(3-1.06) |
mathend000#
Trata-se aqui de determinar o domínio do plano s
mathend000# para o qual F(s)
mathend000# existe, de forma a podermos calcular a TL inversa. Para cada caso específico trata-se de calcular um valor 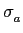 mathend000# real tal que
mathend000# real tal que
Re[F(s)] > 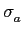 , ,
|
(3-1.07) |
mathend000#
neste caso 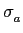 mathend000# é chamada abcissa de convergência absoluta.
mathend000# é chamada abcissa de convergência absoluta.
Exemplo: calcular a abcissa de convergência da função
f (t) = e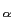 t
mathend000#.
t
mathend000#.
Temos então que
mathend000#
que se pode fácilmente calcular como sendo
F(
s) =
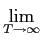
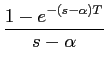
,
mathend000#
e torna-se neste caso claro que F(s)
mathend000# só existe (ou só toma valores finitos) para
s > 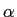 mathend000#, i.e.,
mathend000#, i.e.,
F(
s) =
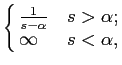
mathend000#
e por isso a abcissa de convergência absoluta é neste caso
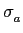 =
= 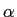 mathend000#.
mathend000#.
Pólos e zeros duma função
Quase todas as funções de variável s
mathend000# que consideraremos podem ser colocadas sob a forma de fração racional
F(s) = 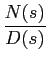 = = 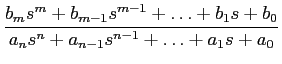 . .
|
(3-1.08) |
mathend000#
De uma forma equivalente podemos exprimir os polinómios N(s)
mathend000# e D(s)
mathend000# em função das suas raízes,
F(s) = 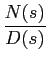 = A = A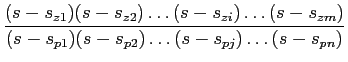 , ,
|
(3-1.09) |
mathend000#
onde A = bm/an
mathend000# é uma constante. A partir de (3-1.9) podemos facilmente determinar as valores de s
mathend000# (em geral complexos) para as quais F(s)
mathend000# toma valores extremos, i.e., valores zero ou valores infinitos, consoante são raízes do numerador ou denominador, e são chamados pólos e zeros respectivamente.
Figura 3.1:
localização de pólos e zeros no plano
complexo: um pólo real (a), dois pólos e um zero reais (b)
e dois pólos imaginários puros complexos conjugados (c).
|
![\includegraphics[width=8cm]{figs/fig4-5.eps}](img159.png) |
Exemplos: vejamos alguns exemplos de TL e a sua representação no plano complexo com a respectiva localização de pólos e zeros.
A)
f (t) = e-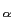 tu(t)
mathend000#
tu(t)
mathend000#
temos que
mathend000#
que tem apenas um pólo para s = - 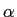 mathend000# como representado na figura 3.1(a).
mathend000# como representado na figura 3.1(a).
B)
f (t) = (e-2t + e-4t)u(t)
mathend000#
temos neste caso que
F(
s) =
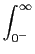 e-(s+2)tdt
e-(s+2)tdt +
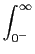 e-(s+4)tdt
e-(s+4)tdt,
mathend000#
de onde utilizando o resultado anterior duas vezes com os devidos valores para 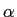 mathend000#,
mathend000#,
mathend000#
com um zero em -3 e dois pólos: um em -4 e outro em -2, conforme representado na figura 3.1(b).
C)
f (t) = cos(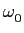 t)u(t)
mathend000#
t)u(t)
mathend000#
F(
s) =
cos(
 t
t)
e-stdt
mathend000#
onde utilizando a forma de Euler,
mathend000#
e utilizando mais uma vez o resultado anterior
mathend000#
e neste caso teremos pólos complexos conjugados no eixo imaginário e um zero em s = 0
mathend000# que se encontram representados na figura 3.1(c).
Teoremas simples da Transformada de Laplace
Na prática mais do que a própria definição, convém conhecer algumas das propriedades mais relavantes da TL, de modo a facilitar a sua aplicação à análise de sistemas.
1. Atraso no domínio temporal: o cálculo da TL de
g(t) = f (t - t0)
mathend000# faz-se através de
TL[
f (
t -
t0)] =
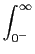 f
f (
t -
t0)
e-stdt,
mathend000#
onde colocando
 = t - t0
mathend000#, e
d
= t - t0
mathend000#, e
d = dt
mathend000# permite escrever
= dt
mathend000# permite escrever
TL[
f (
t -
t0)] =
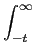 f
f (

)
e-s(t0+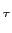 )d
)d
,
mathend000#
e de onde notando que a função causal f (t) = 0
mathend000# para t < 0
mathend000# permite deduzir o resultado final
|
TL[f (t - t0)] = e-st0F(s).
|
(3-1.10) |
mathend000#
2. Diferenciação no domínio de Laplace: demonstra-se facilmente calculando a derivada de
F(s) = 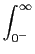 f (t)e-stdt, f (t)e-stdt,
|
(3-1.11) |
mathend000#
em relação a s
mathend000# que é
G(s) = 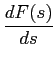 = = 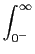 [- tf (t)]e-stdt, [- tf (t)]e-stdt,
|
(3-1.12) |
mathend000#
e portanto temos o par
TL[tf (t)] = - 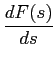 , ,
|
(3-1.13) |
mathend000#
e por dedução à ordem n
mathend000#
TL[(- t)nf (t)] = 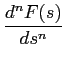 . .
|
(3-1.14) |
mathend000#
3. Família de impulsos: a família de Diracs começa com o degrau unidade
u(t) = u-1(t)
mathend000# para o qual se pode facilmente calcular
TL[u(t)] = 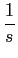 , ,
|
(3-1.15) |
mathend000#
em seguida, utilizando (3-1.14)
TL[tnu(t)] = 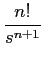 . .
|
(3-1.16) |
mathend000#
Podemos agora generalizar à família de impulsos com a ajuda de (3-1.14)
|
TL[u-n(t)] = s-n.
|
(3-1.17) |
mathend000#
onde u-n(t)
mathend000# designa o integral de ordem n
mathend000# do impulso de Dirac, tal que
u-1(t) = u(t)
mathend000#, u-2(t)
mathend000# será a rampa unitária, etc.
4. Diferenciação temporal: pode-se demonstrar que
TL 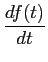 ![$\displaystyle \left.\vphantom{{{df(t)}\over {dt}}}\right]$](img180.png) = sF(s) - f (0-), = sF(s) - f (0-),
|
(3-1.18) |
mathend000#
onde f (0-)
mathend000# representa o valor da função temporal no instante inicial. A demonstração obtem-se fazendo
G(s) = TL 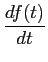 ![$\displaystyle \left.\vphantom{{{df(t)}\over {dt}}}\right]$](img180.png) = =  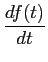 e-stdt, e-stdt,
|
(3-1.19) |
mathend000#
de onde fazendo a mudança de variável dv = df (t)
mathend000# e
u = e-st
mathend000# e integrando por partes,
G(s) = [e-stf (t)]0-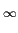 - - 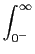 f (t)[- se-st], dt f (t)[- se-st], dt
|
(3-1.20) |
mathend000#
admitindo que f (t)
mathend000# é de tipo exponencial temos que para o extremo superior (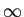 mathend000#) o primeiro termo dá zero e para t = 0-
mathend000# dá f (0-)
mathend000#. Em relação ao segundo termo é fácil ver que se trata de sF(s)
mathend000# e por isso o resultado encontra-se como sendo
mathend000#) o primeiro termo dá zero e para t = 0-
mathend000# dá f (0-)
mathend000#. Em relação ao segundo termo é fácil ver que se trata de sF(s)
mathend000# e por isso o resultado encontra-se como sendo
|
G(s) = - f (0-) + sF(S).
|
(3-1.21) |
mathend000#
As derivadas de ordem superior obtêm-se por extensão do caso precedente tal que
TL 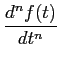 ![$\displaystyle \left.\vphantom{{{d^n f(t)}\over {dt^n}}}\right]$](img184.png) = snF(S) - sn-1f (0-) -...- f(n-1)(0-). = snF(S) - sn-1f (0-) -...- f(n-1)(0-).
|
(3-1.22) |
mathend000#
5. Integração temporal: podemos ver facilmente que
que se demonstra colocando
o que implica g(0-) = 0
mathend000#. Como podemos escrever que a
TL[dg(t)/dt] = TL[f (t)] = F(s)
mathend000#, utilizando (3-1.21), podemos escrever que
TL[dg(t)/dt] = sG(s) - g(0-)
mathend000#. Assim, visto que g(0-) = 0
mathend000# podemos escrever que
F(s) = sG(s)
mathend000# e finalmente provar (3-1.23).
6. Teorema do valor inicial: prova-se que, para as funções sem descontinuidades na origem, podemos determinar o valor da função temporal para t = 0
mathend000# através de
f (0) = 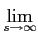 sF(s). sF(s).
|
(3-1.25) |
mathend000#
7. Teorema do valor final: prova-se igualmente que o valor final da função temporal se pode determinar através de
f (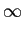 ) = ) = 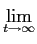 f (t) = f (t) = 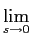 sF(s). sF(s).
|
(3-1.26) |
mathend000#
8. TL do produto de convolução: consideremos o produto de convolução entre duas funções f1(t)
mathend000# e f2(t)
mathend000# tal que
| TL[f1(t) * f2(t)] |
= |
  f1( f1( )f2(t - )f2(t -  )d )d e-stdt e-stdt |
|
| |
= |
  f1( f1( )f2( )f2(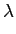 )e-s( )e-s(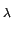 + +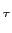 )d )d d d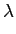 |
|
| |
= |
 f1( f1( )e-s )e-s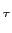 d d  f2( f2(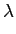 )e-s )e-s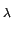 d d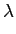 |
|
| |
= |
F1(s)F2(s) |
(3-1.27) |
onde foi utilizada a mudança de variável
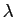 = t -
= t -  mathend000# com a respectiva alteração no integral. Assim podemos ver que a TL do produto de convolução entre dois sinais, resulta no produto simples das TL dos sinais.
mathend000# com a respectiva alteração no integral. Assim podemos ver que a TL do produto de convolução entre dois sinais, resulta no produto simples das TL dos sinais.
9. Funções periódicas causais: é frequente na prática querermos determinar a TL de uma função periódica. Tomemos como exemplo o caso simples de uma função
g(t) = f (t) + f (t - T)
mathend000#, resultante da repetição da função f (t)
mathend000# com um intervalo T
mathend000#. Assim podemos directamente escrever
G(s) = TL[g(t)] = TL[f (t)] + TL[f (t)]e-sT,
mathend000#
onde utilizámos (3-1.10). Ou ainda
|
G(s) = F(s)[1 + e-sT].
|
(3-1.28) |
mathend000#
A partir deste caso simples deduzimos directamente o caso geral do sinal periódico causal onde se o sinal g(t)
mathend000# se escrever
g(t) = 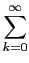 f (t - kT), f (t - kT),
|
(3-1.29) |
mathend000#
então, a partir de (3-1.28), temos que
G(
s) =
F(
s)
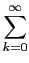 e-kTs
e-kTs
mathend000#
ou ainda, utilizando o desenvolvimento em série de 1/(1 - x)
mathend000# para
|x|< 1
mathend000# (ver D.3),
Exemplo: queremos determinar a TL da função periódica causal e limitada no tempo dada por
g(
t) =
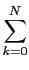 f
f (
t -
kT)
mathend000#
A solução deste problema pode obter-se através da utilização de (3-1.30) tal que
g(
t) =
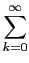 f
f (
t -
kT) -
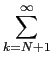 f
f (
t -
kT),
mathend000#
onde a TL do segundo termo é uma soma de termos de uma progressão geométrica de razão e-Ts
mathend000# e cujo primeiro termo é
e(N+1)Ts
mathend000#. Assim podemos escrever que
TL[
g(
t)] =
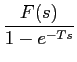
-
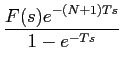
mathend000#
ou mais condensado
G(
s) =
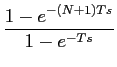 F
F(
s).
mathend000#
que é o resultado procurado.
Transformada de Laplace Inversa
A definição da Transformada de Laplace Inversa (TLI) foi dada em (3-1.3). A necessidade do cálculo da TLI é evidentemente a de permitir a obtenção da (ou das) função (ões) temporal (ais) resultado da análise complexa do sistema. Existem fundamentalmente duas formas de resolver (3-1.3): uma através da integração directa e outra através do reconhecimento da unicidade da TL. O primeiro método é geralmente extremamente trabalhoso pois implica o cálculo dos resíduos para cada pólo simples da função
F(s)est
mathend000# e para um determinado contorno no plano s
mathend000# - este método apesar de ser bastante elegante não é quase nunca utilizado. Em vez disso, utiliza-se o segundo método que consiste em considerar que f (t)
mathend000# e F(s)
mathend000# formam um par único e por isso se
TL[f (t)] = F(s)
mathend000# então temos que
TLI[F(s)] = f (t)
mathend000#. Por isso basta-nos colocar F(s)
mathend000# sob uma forma cuja a função temporal é conhecida. Em geral sob a forma da soma de vários termos que são transformadas de Laplace de funções temporais conhecidas para podermos dizer que o sinal temporal resultante f (t)
mathend000# não é mais do que a soma dessas funções temporais.
Exemplos:
A) consideremos o caso da função simples,
F(s) = 10s-1,
mathend000#
portanto
f (t) = 10u(t)
mathend000#, porque já tinhamos visto que
TL[u(t)] = 1/s
mathend000#.
B) ou o caso da função
G(
s) =
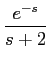
,
mathend000#
onde, sabendo que a TL de um atraso puro é


(
t - 1)
e-stdt =
e-s,
mathend000#
e que
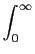 e-2te-stdt
e-2te-stdt =
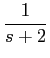
,
mathend000#
podemos deduzir que
f (t) = e-2(t-1)u(t - 1).
mathend000#
No caso de funções mais complexas (frequentes na prática) torna-se difícil identificar os inversos por observação directa. Na maior parte dos casos trata-se de frações racionais complexas e a sua inversão passa pela decomposição em termos simples cujos inversos sejam conhecidos, como por exemplo, a função
F(
s) =
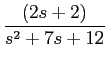
,
mathend000#
que se pode decompor em fracções simples como
mathend000#
onde os coeficientes A1
mathend000# e A2
mathend000# podem ser determinados multiplicando ambos os termos da equação anterior por s + 3
mathend000# e fazendo s = - 3
mathend000# e s + 4
mathend000# e fazendo s = - 4
mathend000#, respectivamente. Obtendo-se neste caso A1 = - 4
mathend000# e A2 = 6
mathend000#. A partir deste valores podemos então escrever que
f (t) = [- 4e-3t +6e-4t]u(t),
mathend000#
que é o resultado esperado. Existem várias técnicas de cálculo para a decomposição de fracções racionais que deixamos ao cuidado do leitor, mediante uma atenta revisão do programa da disciplina de Análise Matemática.
Aplicação aos sistemas lineares
A utilização prática da TL na análise e síntese de sistemas lineares passa essencialmente pelas seguintes propriedades:
TL[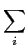 aifi(t)] = aifi(t)] = 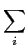 aiFi(s), aiFi(s),
|
(3-2.01) |
mathend000#
e
|
TL[f(n)(t)] = snF(s) - sn-1f (0) -...- sf(n-2)(0) - f(n-1)(0),
|
(3-2.02) |
mathend000#
com as quais as equações diferenciais em t
mathend000# se tornam equações algébricas em s
mathend000#. Na prática o problema é quase sempre dividido em cinco etapas sucessivas:
1) transformar a equação diferencial numa equação algébrica utilizando (3-2.2)
2) resolver a equação resultante para a grandeza de saída Y(s)
mathend000#
3) desenvolver Y(s)
mathend000# em frações racionais
4) encontrar o inverso
y(t) = TLI[Y(s)]
mathend000#
5) verificar o resultado
Exemplos:
A) Seja a seguinte equação diferencial de primeira ordem
a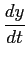
+
by =
x(
t),
mathend000#
com
x(t) = e-ctu(t)
mathend000#. Podemos desde já escrever a passagem para o domínio s
mathend000#,
a[
sY(
s) -
y(0)] +
bY(
s) =
X(
s) =
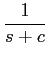
,
mathend000#
isto é
Y(
s) =
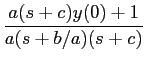
,
mathend000#
ou também, decompondo em fracções racionais
Y(
s) =
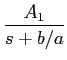
+
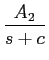
,
mathend000#
com
A1 =
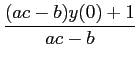 A2
A2 =
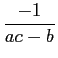
,
mathend000#
e de onde se pode deduzir o resultado
y(t) = [A1e-bt/a + A2e-ct]u(t).
mathend000#
A verificação do resultado faz-se, óbviamente, inserindo y(t)
mathend000# na equação diferencial inicial. Alternativamente poderíamos
utilizar os teoremas dos valores inicial e final, (3-1.25) e (3-1.26), respectivamente, para verificar o comportamento assimptótico da solução obtida.
B) seja agora a equação diferencial de segunda ordem
i''(t) + 7i'(t) + 10i(t) = 6e-3tu(t),
mathend000#
com i(0) = 3
mathend000# A e i'(0) = 3
mathend000# A/s. Podemos então escrever, calculando a TL de ambos os termos,
s2I(
s) -
si(0) -
i'(0) + 7
sI(
s) - 7
i(0) + 10
I(
s) =
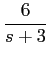
,
mathend000#
de onde, resolvendo em relação a I(s)
mathend000#,
mathend000#
e portanto a solução final
i(t) = 8e-2t -3e-3t -2e-5t, t > 0.
mathend000#
Na prática somos levados a considerar frequentemente, não uma equação única para determinar uma das variáveis do sistema, mas sim um conjunto de equações com várias variáveis, em geral ligadas entre elas, e por isso teremos de colocar o problema sob a forma de um sistema de equações.
Exemplo: considere o seguinte sistema de equações diferenciais,
mathend000#
mathend000#
com condições iniciais nulas, i.e.,
x(0) = y(0) = 0
mathend000#. Aplicando a TL nos dois membros de cada uma das equações acima obtemos,
(
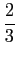 s
s + 1)
X(
s) -
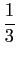 sY
sY(
s) =
F(
s) =
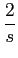
mathend000#
-
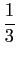 sX
sX(
s) + (
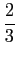 s
s + 1)
Y(
s) = 0,
mathend000#
das quais podemos deduzir por substituição
mathend000#
mathend000#
e finalmente aplicando a TLI,
x(t) = (2 - e-t - e-3t)u(t),
mathend000#
y(t) = (e-t - e-3t)u(t),
mathend000#
de onde podemos facilmente verificar as condições iniciais.
Função de sistema
Podemos agora fazer uma generalização dos sistemas lineares de primeira e segunda ordem ao caso de uma ordem superior n
mathend000#. Assim podemos dizer que a relação entre a entrada x(t)
mathend000# e a saída y(t)
mathend000# de um sistema linear pode ser descrita por uma equação do tipo1
Neste caso, e para condições iniciais nulas, temos que tomando a TL de ambos os termos,
onde, considerando condições iniciais nulas,
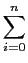 aisiY(s) = aisiY(s) = 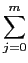 bjsjX(s), bjsjX(s),
|
(3-2.05) |
mathend000#
rearranjando os termos e desenvolvendo os somatórios
Y(s) = 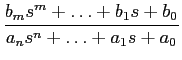 X(s). X(s).
|
(3-2.06) |
mathend000#
Daqui podemos deduzir a função de sistema, ou função de transferência, H(s)
mathend000#,
H(s) = 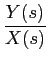 = = 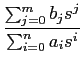 . .
|
(3-2.07) |
mathend000#
No caso em que os pólos são todos simples, a função de transferência H(s)
mathend000# pode ser representada sob a forma de
H(s) = 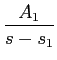 + + 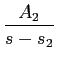 +...+ +...+ 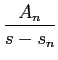 , ,
|
(3-2.08) |
mathend000#
onde a sua TLI se escreve
|
h(t) = A1es1t + A2es2t +...+ Anesnt,
|
(3-2.09) |
mathend000#
que é chamada a resposta impulsiva do sistema, i.e., é a resposta do sistema Y(s)
mathend000# quando o sinal de entrada é um impulso de Dirac, e então visto que
TL[x(t) = 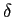 (t)] = 1
mathend000#, temos que Y(s) = H(s)
mathend000#. Isto significa que a resposta impulsiva depende apenas da função de transferência H(s)
mathend000# e por isso apenas do sistema ele mesmo e, em particular, dos pólos do sistema
si;i = 1,..., n
mathend000#. Também isto não é estranho pois os pólos do sistema são aqueles que estão ligados à resposta natural do sistema, i.e., a resposta do sistema sem excitação - também chamada solução da equação homógenea.
(t)] = 1
mathend000#, temos que Y(s) = H(s)
mathend000#. Isto significa que a resposta impulsiva depende apenas da função de transferência H(s)
mathend000# e por isso apenas do sistema ele mesmo e, em particular, dos pólos do sistema
si;i = 1,..., n
mathend000#. Também isto não é estranho pois os pólos do sistema são aqueles que estão ligados à resposta natural do sistema, i.e., a resposta do sistema sem excitação - também chamada solução da equação homógenea.
Exemplos:
A) sistema de primeira ordem sem condições iniciais: considere a figura 3.2, com y(0) = 0
mathend000# e
x(t) = e-2tu(t).
mathend000#
Figura 3.2:
sistema de primeira ordem.
|
![\includegraphics[width=8cm]{figs/fig4-6.eps}](img238.png) |
Podemos directamente escrever
x(
t) =
C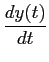
+
y(
t),
mathend000#
a partir da qual tiramos a TL
X(s) = CsY(s) + Y(s),
mathend000#
de onde a função do sistema H(s)
mathend000# é
H(
s) =
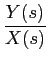
=
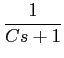
.
mathend000#
Desta podemos determinar a resposta impulsiva h(t)
mathend000#, que se escreve
h(
t) =
TLI[
H(
s)] =
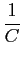 e-t/Cu
e-t/Cu(
t),
mathend000#
e sabendo que
X(
s) =
TL[
X(
t)] =
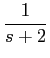
,
mathend000#
portanto Y(s)
mathend000# escreve-se
mathend000#
e finalmente
y(
t) = [
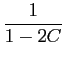 e-2t
e-2t +
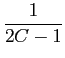 e-t/C
e-t/C]
u(
t),
mathend000#
será a resposta do circuito no caso em que o sistema se encontra inerte no momento inicial, i.e., quando y(0) = 0
mathend000#.
B) sistema de primeira ordem com condições iniciais: considere o mesmo sistema da figura 3.2 mas agora com um valor inicial da saída y(0) = 2
mathend000#.
Não será necessário re-escrever todas as equações, mas sómente a TL da equação diferencial tendo em conta (3-1.22),
X(s) = C[sY(s) - y(0)] + Y(s),
mathend000#
substituindo pelos valores númericos e pela transformada de X
mathend000# obtemos
Y(
s) =
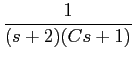
+
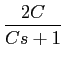
,
mathend000#
utlizando o resultado da decomposição do caso anterior, obtemos
y(
t) =
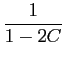 e-2t
e-2t +
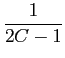 e-t/C
e-t/C +2
e-t/C![$\displaystyle \left.\vphantom{{1\over {1-2C}}e^{-2t} + {1\over {2C-1}}e^{-t/C} + 2e^{-t/C}}\right]$](img249.png) u
u(
t),
mathend000#
onde simplificando
mathend000#
C) sistema de segunda ordem sem condições iniciais: considere agora o caso do sistema da figura 3.3 com
x(t) = 5e-2tu(t)
mathend000#. Pretende-se calcular a saída y(t)
mathend000#.
Figura 3.3:
sistema de segunda ordem.
|
![\includegraphics[width=10cm]{figs/fig4-7.eps}](img253.png) |
Como anteriormente, podemos escrever directamente
mathend000#
cuja TL é dada por
Y(s)(s2 + 2s + 2) = 2(s + 1)X(s),
mathend000#
visto que
X(s) = TL[x(t)]
mathend000# é dada por
X(
s) =
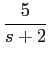
,
mathend000#
temos que, por substituição na equação anterior, e cálculo das raízes da equação do segundo grau do denominador
Y(
s) =
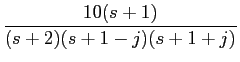
,
mathend000#
dando origem à representação no plano s
mathend000# da figura 3.4. A inversão faz-se por decomposição da fração polinomial,
mathend000#
onde podemos facilmente deduzir que
A1 = - 5,
B1 =
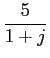
,
mathend000#
com
B2 = B1 *
mathend000#. Por questões de simplificação do cálculo é frequente colocar os coeficientes complexos sob forma exponencial. Assim podemos escrever que
B1 =
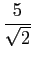 e
e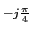
,
mathend000#
e portanto
mathend000#
Podemos agora calcular a TLI a cada um dos termos para obter
y(
t) = - 5
e-2t +
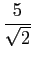
[
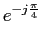 e(-1+j)t
e(-1+j)t +
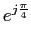 e(-1-j)t
e(-1-j)t]
u(
t),
mathend000#
ou ainda simplificando
y(
t) = - 5
e-2t +
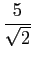 e-t
e-t[
e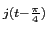
+
e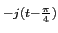
]
u(
t),
mathend000#
de onde deduzimos finalmente
y(
t) = [5
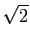 e-t
e-tcos(
t -
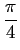
) - 5
e-2t]
u(
t).
mathend000#
Neste resultado final podemos facilmente identificar que o primeiro termo - oscilação em cos(t)
mathend000# - é a resposta do sistema em regime permanente e o segundo - exponencial atenuada - é a resposta ao sinal de entrada x(t)
mathend000#.
Figura 3.4:
pólos e zeros no plano s
mathend000#.
|
![\includegraphics[width=8cm]{figs/fig4-8.eps}](img274.png) |
O integral de Fourier, ou simplesmente transformada de Fourier (TF), permite passar de uma função temporal s(t)
mathend000# `qualquer' (periódica ou aperiódica) para uma função frequencial S( )
mathend000# definida por
)
mathend000# definida por
S( ) = TF[s(t)] = ) = TF[s(t)] =  s(t)e-j s(t)e-j tdt. tdt.
|
(3-3.01) |
mathend000#
Em geral a S( )
mathend000# chama-se espectro de s(t)
mathend000#, mesmo se essa designação deva ser reservada para
|S(
)
mathend000# chama-se espectro de s(t)
mathend000#, mesmo se essa designação deva ser reservada para
|S( )|
mathend000#, que é tambem chamada densidade espectral em amplitude. De modo análogo a transformada de Fourier inversa (TFI) é definida por
)|
mathend000#, que é tambem chamada densidade espectral em amplitude. De modo análogo a transformada de Fourier inversa (TFI) é definida por
s(t) = TFI[S( )] = )] = 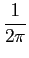  S( S( )ej )ej td td , ,
|
(3-3.02) |
mathend000#
que permite determinar a função temporal s(t)
mathend000# de modo único a partir do seu espectro S( )
mathend000#. Por vezes é mais cómodo representar o espectro de s(t)
mathend000# como uma função da frequência (em Hz) e não da pulsação em rd/s e por isso de forma análoga temos
)
mathend000#. Por vezes é mais cómodo representar o espectro de s(t)
mathend000# como uma função da frequência (em Hz) e não da pulsação em rd/s e por isso de forma análoga temos
S(f )= TF[s(t)] =  s(t)e-j2 s(t)e-j2 ftdt. ftdt.
|
(3-3.03) |
mathend000#
e
s(t) = TFI[S(f )] =  S(f )ej2 S(f )ej2 ftdf, ftdf,
|
(3-3.04) |
mathend000#
onde obviamente
f =  /2
/2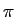 mathend000#.
mathend000#.
No caso de um sinal de variável (tempo) discreta, a sua Transformada de Fourier (em inglês Discrete Time Fourier Transform ou DTFT) obtem-se fazendo a passagem t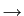 nT
mathend000# - onde T
mathend000# é o período de amostragem e n
mathend000# é uma variável discreta - transformando-se assim o integral em somatório, permitindo escrever a partir de (3-3.1)
nT
mathend000# - onde T
mathend000# é o período de amostragem e n
mathend000# é uma variável discreta - transformando-se assim o integral em somatório, permitindo escrever a partir de (3-3.1)
S( ) = ) = 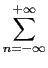 s(nT)e-j s(nT)e-j nT. nT.
|
(3-3.05) |
mathend000#
note-se o facto de que se nesta equação substituirmos  mathend000# por
mathend000# por
 +2
+2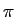 /T
mathend000# obtemos,
/T
mathend000# obtemos,
S( + + 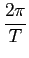 ) ) |
= |
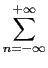 s(nT)e s(nT)e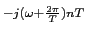 |
|
| |
= |
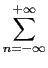 s(nT)e-j s(nT)e-j nT-2 nT-2 n n |
|
| |
= |
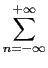 s(nT)e-j( s(nT)e-j( nT) nT) |
|
| |
= |
S( ), ), |
(3-3.06) |
dado que
exp(-2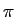 n) = 1
mathend000# para qualquer valor de n
mathend000# inteiro. Chega-se então à conclusão interessante de que, independentemente de s(nT)
mathend000# ser periódico ou não, o seu espectro é sempre periódico de período 2
n) = 1
mathend000# para qualquer valor de n
mathend000# inteiro. Chega-se então à conclusão interessante de que, independentemente de s(nT)
mathend000# ser periódico ou não, o seu espectro é sempre periódico de período 2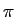 /T
mathend000#, onde T
mathend000# é o intervalo de amostragem (intervalo de tempo entre duas amostras consecutivas). Devemos aqui sublinhar que esta é sem dúvida a maior e, quase única, diferença entre a TF de sinais contínuos e sinais discretos.
/T
mathend000#, onde T
mathend000# é o intervalo de amostragem (intervalo de tempo entre duas amostras consecutivas). Devemos aqui sublinhar que esta é sem dúvida a maior e, quase única, diferença entre a TF de sinais contínuos e sinais discretos.
Tendo em conta esta propriedade a TF inversa no caso discreto obtem-se a partir de (3-3.2), tendo em conta que devido à periodicidade do espectro, apenas devemos considerar o integral de definição num período
s(nT) = 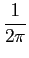 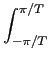 S( S( )ej )ej nTd nTd . .
|
(3-3.07) |
mathend000#
- Sinal analítico, f (t)
mathend000# complexo: se o sinal temporal f (t)
mathend000# é complexo com uma parte real fR(t)
mathend000# e uma parte imaginária fX(t)
mathend000# pode-se então demonstrar facilmente que
R( ) = ) =  [fR(t)cos [fR(t)cos t + fX(t)sin t + fX(t)sin t]dt, t]dt,
|
(3-3.08) |
mathend000#
e
X( ) = - ) = -  [fR(t)sin [fR(t)sin t - fX(t)cos t - fX(t)cos t]dt, t]dt,
|
(3-3.09) |
mathend000#
onde
F( ) = R(
) = R( ) + jX(
) + jX( )
mathend000#, e inversamente
)
mathend000#, e inversamente
fR(t) = 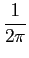  [R( [R( )cos )cos t - X( t - X( )sin )sin t]d t]d , ,
|
(3-3.10) |
mathend000#
e
fX(t) = 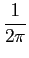  [R( [R( )sin )sin t + X( t + X( )cos )cos t]d t]d . .
|
(3-3.11) |
mathend000#
Estas relações fazem aparecer propriedades interessantes quando fX(t)
mathend000# é vista como a transformada de Hilbert de f (t)
mathend000# que é o sinal analítico (ver disciplina de Fundamentos de Telecomunicações).
- Sinal f (t)
mathend000# real: neste caso temos obviamente
fR(t) = f (t)
mathend000# e fX(t) = 0
mathend000#, o que implica que
R( ) = ) = 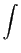 f (t)cos f (t)cos tdt tdt
|
(3-3.12) |
mathend000#
e
X( ) = - ) = - 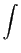 f (t)sin f (t)sin tdt tdt
|
(3-3.13) |
mathend000#
de onde se pode deduzir que
R( ) = R(-
) = R(-  )
mathend000# e
X(
)
mathend000# e
X( ) = - X(-
) = - X(-  )
mathend000#. Isto quer dizer que
F(-
)
mathend000#. Isto quer dizer que
F(-  ) = F * (
) = F * ( )
mathend000# o que consiste numa propriedade importante da transformada de Fourier das funções reais. O inverso também se pode demonstrar, ou seja, que se o espectro frequencial de uma função obedece a
F(-
)
mathend000# o que consiste numa propriedade importante da transformada de Fourier das funções reais. O inverso também se pode demonstrar, ou seja, que se o espectro frequencial de uma função obedece a
F(-  ) = F * (
) = F * ( )
mathend000# então f (t)
mathend000# é real.
)
mathend000# então f (t)
mathend000# é real.
- Sinal temporal par e real: neste caso, em que o sinal real
f (t) = f (- t)
mathend000#, temos que
R( ) = ) =  f (t)cos f (t)cos tdt = 2 tdt = 2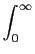 f (t)cos( f (t)cos( t)dt, t)dt,
|
(3-3.14) |
mathend000#
e
X( ) = 0, ) = 0,
|
(3-3.15) |
mathend000#
devido ao facto que o produto de duas funções pares dá ainda uma função par, e o produto de uma função par e uma função ímpar dá uma função ímpar. Portanto a TF de uma função real par é real. Inversamente a TFI de uma função real é uma função também real e par.
- Sinal temporal ímpar: neste caso
f (t) = - f (- t)
mathend000#, e por analogia com o caso precedente
R( ) = 0, ) = 0,
|
(3-3.16) |
mathend000#
e
X( ) = - 2 ) = - 2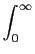 f (t)sin f (t)sin tdt. tdt.
|
(3-3.17) |
mathend000#
- TF do produto de convolução: vamos agora demonstrar que o produto simples de duas funções no domínio do tempo é um produto de convolução no domínio da frequência e vice-versa uma convolução no tempo transforma-se numa simples multiplicação na frequência. Pretende-se portanto demonstrar o seguinte teorema
Se
|
X1(f )= TF[x1(t)] e X2(f )= TF[x2(t)],
|
(3-3.18) |
mathend000#
então
TF[ x1(t - x1(t -  )x2( )x2( )d )d ] ] |
= |
TF[x1(t) * x2(t)] |
|
| |
= |
X1(f )X2(f ). |
(3-3.19) |
A demonstração deste teorema faz-se a partir da equação (3-3.19),
TF[x1(t) * x2(t)] =   x1(t - x1(t -  )x2( )x2( )d )d e-j2 e-j2 ftdt, ftdt,
|
(3-3.20) |
mathend000#
na qual poderemos inverter a ordem de integração considerando que ambos os integrais convergem nos respectivos intervalos (sinais de energia finita) e fazendo a mudança de variável v = t -  mathend000# e assim,
mathend000# e assim,
TF[x1(t) * x2(t)] =   x1(v)x2( x1(v)x2( )e-j2 )e-j2 f(v+ f(v+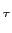 )d )d dv, dv,
|
(3-3.21) |
mathend000#
ou seja
TF[x1(t) * x2(t)] =  [ [ x1(v)e-j2 x1(v)e-j2 fvdv]x2( fvdv]x2( )e-j2 )e-j2 f f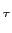 d d , ,
|
(3-3.22) |
mathend000#
e na qual podemos reconhecer que o termo entre [ ]
mathend000# é a TF de x1(t)
mathend000# que pode sair do integral em  mathend000# ficando
mathend000# ficando
| TF[x1(t) * x2(t)] |
= |
X1(f ) x2( x2( )e-j2 )e-j2 f f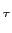 d d |
|
| |
= |
X1(f )X2(f ), |
(3-3.23) |
o que demonstra o teorema. A relação utilizada neste teorema foi a forma geral da convolução na qual ambos os sinais eram supostos não causais. No caso de sinais causais os limites inferior e superior do integral de convolução serão, em princípio, 0
mathend000# e t
mathend000# respectivamente, mas podem ser substituidos por - 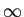 mathend000# e
mathend000# e 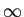 mathend000# o que não altera o valor do integral visto que o produto dos dois sinais é nulo entre
[-
mathend000# o que não altera o valor do integral visto que o produto dos dois sinais é nulo entre
[-  , 0]
mathend000# e
[t,
, 0]
mathend000# e
[t, ]
mathend000#.
]
mathend000#.
- TF do produto ordinário: já vimos que a TF do produto de convolução no tempo resulta num produto simples no domínio da frequência. Vamos agora ver qual a TF do produto simples no tempo.
Seja,
| TF[x1(t) . x2(t)] |
= |
 [ [ X1(v)ej2 X1(v)ej2 vtdv]x2(t)e-j2 vtdv]x2(t)e-j2 ftdt ftdt |
|
| |
= |
 X1(v) X1(v) x2(t)e-j2 x2(t)e-j2 (f-v)tdtdv (f-v)tdtdv |
|
| |
= |
 X1(v)X(f - v)dv X1(v)X(f - v)dv |
|
| |
= |
X1(f ) * X2(f ) |
(3-3.24) |
que nos permite dizer que a TF do produto simples no tempo é igual ao produto de convolução no domínio da frequência. Obviamente que tanto para esta relação como para a estabelecida no ponto anterior o inverso também é verdade, dado que a TF é uma transformação injectiva.
Devido à sua importância na manipulação de sinais, devemos ainda referir como se escrevem estas expressões quando da utilização da TF em  mathend000#. Assim podemos facilmente demonstrar que
mathend000#. Assim podemos facilmente demonstrar que
TF[x1(t) * x2(t)] = X1( )X2( )X2( ), ),
|
(3-3.25) |
mathend000#
e
TF[x1(t) . x2(t)] = 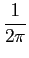 X1( X1( ) * X2( ) * X2( ). ).
|
(3-3.26) |
mathend000#
1. Função porta rectangular - rect(x)
Talvez a função mais utilizada em teoria do sinal seja a função de observação ou ``função porta rectangular''
Neste caso obtém-se
TF[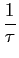 rect( rect(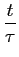 )] )] |
= |
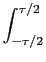 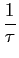 e-j e-j tdt tdt |
|
| |
= |
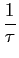 [ [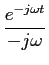 ]- ]-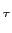 /2 /2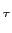 /2, /2, |
(3-3.28) |
o que, utilizando a relação,
sin x = 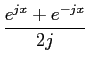 , ,
|
(3-3.29) |
mathend000#
dá como resultado
TF[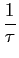 rect( rect(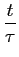 )] )] |
= |
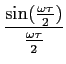 |
|
| |
= |
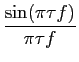 |
|
| |
= |
sinc( f ) f ) |
(3-3.30) |
O que em resumo nos define que a TF da função porta é uma sinc (ver figura 3.5),
TF[rect(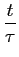 )] = )] =  sinc( sinc( f ), f ),
|
(3-3.31) |
mathend000#
e inversamente
TFI[sinc( f )] = f )] = 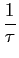 rect( rect(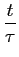 ). ).
|
(3-3.32) |
mathend000#
Figura 3.5:
Transformada de Fourier da função porta rectangular (a) na função sinc (b).
|
![\includegraphics[width=10cm]{figs/TF_plots1.eps}](img293.png) |
No caso discreto temos um resultado semelhante. Assim a TF da função rect discreta definida por
rect(k/K) = 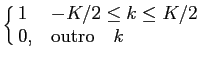
|
(3-3.33) |
mathend000#
calcula-se através de
TF[rect(k/K)] = 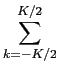 e-j2 e-j2 fkT, fkT,
|
(3-3.34) |
mathend000#
de onde fazendo n = k + K/2
mathend000# permite escrever
| TF[rect(k/K)] |
= |
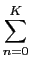 e-j2 e-j2 f(n-K/2)T, f(n-K/2)T, |
|
| |
= |
ej fKT fKT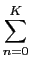 e-j2 e-j2 fnT, fnT, |
(3-3.35) |
onde o somatório é uma progressão geométrica de razão
e-j2 fT
mathend000# e por isso pode ser escrita como
fT
mathend000# e por isso pode ser escrita como
TF[rect(k/K)] = ej fKT fKT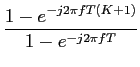 , ,
|
(3-3.36) |
mathend000#
onde podemos agora manipular a expressão de forma a fazer aparecer um seno no numerador e no denominador. Primeiramente, multiplicando e dividindo por
exp(j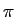 fT)
mathend000# e colocando
exp(-j
fT)
mathend000# e colocando
exp(-j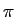 fT)
mathend000# em factor no denominador obtemos
fT)
mathend000# em factor no denominador obtemos
| TF[rect(k/K)] |
= |
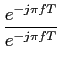 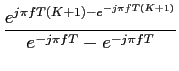 , , |
|
| |
= |
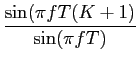 , , |
|
| |
= |
(K + 1)![$\displaystyle {{{\rm sinc} [fT(K+1)]}\over {{\rm sinc} (fT)}}$](img301.png) , , |
(3-3.37) |
e que, como se pode ver, resulta num rácio entre duas sinc's, uma de abertura T(K + 1)
mathend000# e outra de abertura T
mathend000#, multiplicado por um termo de amplitude de K + 1
mathend000# (ver figura 3.6).
Figura 3.6:
Transformada de Fourier da função porta rectangular discreta no tempo: com K = 11
mathend000# amostras (a) função sinc na frequência (b).
|
![\includegraphics[width=10cm]{figs/TF_plots2.eps}](img302.png) |
2. Função sinc(x)
Dado que é bastante difícil calcular a TF da função sinc(x) (ver apêndice E para mais detalhes) vamos proceder ao contrário, i.e., calcular a TF inversa da função porta no domínio da frequência. Seja então a TFI
TFI[rect( f )] f )] |
= |
 rect( rect( f )ej2 f )ej2 ftdf ftdf |
|
| |
= |
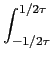 ej2 ej2 ftdf ftdf |
|
| |
= |
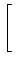 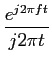 ![$\displaystyle \left.\vphantom{{{e^{j2\pi ft}}\over {j2\pi t}}}\right]_{{-1/2\tau}}^{{1/2\tau}}$](img306.png) |
|
| |
= |
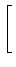 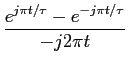 ![$\displaystyle \left.\vphantom{{{e^{j\pi t/\tau}-e^{-j\pi t/\tau}}\over {-j2\pi t}}}\right]$](img309.png) |
|
| |
= |
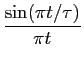 |
|
| |
= |
 sinc(t/ sinc(t/ ), ), |
(3-3.38) |
o que nos revela o interessante resultado de que a TFI da função porta é uma sinc, ou por outras palavras a TF da sinc é uma função porta,
TF[sinc(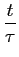 )] = )] = 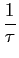 rect( rect( f ), f ),
|
(3-3.39) |
mathend000#
e vice-versa
TFI[rect( f )] = f )] =  sinc( sinc(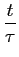 ). ).
|
(3-3.40) |
mathend000#
Exercício: calcular a TFI da função porta no domínio da frequência seguindo sensivelmente os mesmos passos da equação (3-3.38), mas agora para o caso discreto no tempo.
3. Gaussiana
Calculemos agora a TF da função
g(t) = 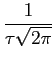 e e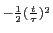 . .
|
(3-3.41) |
mathend000#
Devido à dificuldade de integrar a exponencial num intervalo infinito deveremos, para começar, fazer aparecer no exponente um quadrado puro. Assim
G( ) = ) =  g(t)e-j g(t)e-j tdt = tdt =  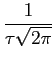 e e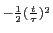 e-j e-j tdt, tdt,
|
(3-3.42) |
mathend000#
cujo expoente é
e ao qual, para fazer aparecer um quadrado puro, é necessário adicionar e subtrair o termo
- 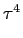
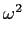 mathend000# obtendo assim
Sabendo que
obtém-se o resultado final depois de simplificação,
mathend000# obtendo assim
Sabendo que
obtém-se o resultado final depois de simplificação,
G( ) = e ) = e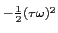 , ,
|
(3-3.46) |
mathend000#
que é ainda uma Gaussiana no domínio da frequência.
A tratamento clássico da transformada de Fourier não contempla o caso das funções não aperiódicas, isto é, das funções não limitadas no tempo porque, matematicamente o integral de definição não converge. São exemplos o caso da família de impulsos das funções generalizadas que passamos a descrever.
No caso do valor infinito do Dirac o integral não existe, mas como só o caso limite nos interessa, o tratamento matemático faz-se por aproximação. Deseja-se calcular a TF do sinal 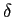 (t)
mathend000#. Muito simplesmente,
(t)
mathend000#. Muito simplesmente,
TF[ (t)] (t)] |
= |
 ( ( ) ) |
|
| |
= |
  (t)e-j (t)e-j tdt tdt |
|
| |
= |
e-j 0 = 1, 0 = 1, |
(3-5.1) |
devido à propriedade (2-3.13) tomada no ponto zero. Inversamente
| TFI[1] |
= |
  1ej 1ej td td |
|
| |
= |
 (t). (t). |
(3-5.2) |
Impõe-se agora estabelecer as expressões recíprocas das precedentes, i.e., as TF de 1 e TFI de
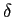 (
( )
mathend000#. A partir de (3-5.2) mudando a variável de integração de
)
mathend000#. A partir de (3-5.2) mudando a variável de integração de  mathend000# em - t
mathend000# e notando que o impulso de Dirac é uma função par, é fácil escrever
mathend000# em - t
mathend000# e notando que o impulso de Dirac é uma função par, é fácil escrever
| TF[1] |
= |
 1e-j 1e-j tdt tdt |
|
| |
= |
2  ( ( ), ), |
(3-5.3) |
e inversamente
TFI[ ( ( )] )] |
= |
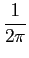   ( ( )ej )ej td td |
|
| |
= |
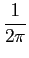 . . |
(3-5.4) |
Por vezes cria-se alguma confusão na obtenção destes resultados, devido à alternância entre a utilização da pulsação  mathend000# em vez da frequência f
mathend000#. Repetimos agora os mesmos resultados mas utilizando a variável f
mathend000#.
mathend000# em vez da frequência f
mathend000#. Repetimos agora os mesmos resultados mas utilizando a variável f
mathend000#.
TF do Dirac,
TF[ (t)] = (t)] =   (t)e-j2 (t)e-j2 ftdt = e-j2 ftdt = e-j2 f0 = 1 f0 = 1
|
(3-5.5) |
mathend000#
TFI de 1,
| TFI[1] = |
= |
 1ej2 1ej2 ftdf ftdf |
|
| |
= |
 (t). (t). |
(3-5.6) |
TF de 1,
| TF[1] |
= |
 1e-j2 1e-j2 ftdt ftdt |
|
| |
= |
 (f ), (f ), |
(3-5.7) |
e inversamente
TFI[ (f )] (f )] |
= |
  (f )ej2 (f )ej2 ftdf ftdf |
|
| |
= |
1. |
(3-5.8) |
O cálculo da transformada de Fourier (TF) da função degrau unidade u(t)
mathend000# ultrapassa largamente o âmbito desta disciplina, pois necessita o conhecimento de algumas ferramentas aplicáveis a funções generalizadas (ou distribuições) das quais o Dirac é um exemplo. Uma dessas ferramentas, necessária neste caso, é a noção de integral limite de Cesaro. Quando um integral é divergente no sentido usual de Rieman é possível, nalguns casos práticos, obter convergência, multiplicando a função integral por um ``factor de convergência'', assim, no sentido de limite de Cesaro - indicado pelo símbolo (C) antes do integral -
(C)  g(t)dt = g(t)dt = 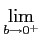  g(t)e-b|t|dt, g(t)e-b|t|dt,
|
(3-6.1) |
mathend000#
onde
e-b|t|
mathend000# é o factor de convergência. No nosso caso, calcularemos o integral
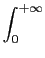 sin(at)dt, sin(at)dt,
|
(3-6.2) |
mathend000#
no limite de Cesaro, através de
(C) 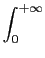 sin(at)dt sin(at)dt |
= 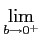 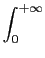 sin(at)e-btdt sin(at)e-btdt |
| |
= 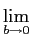 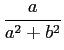 |
| |
= 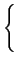 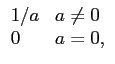 |
|
(3-6.3) |
mathend000#
e escrever simplesmente
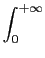 sin(at)dt = sin(at)dt = 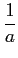 . .
|
(3-6.4) |
mathend000#
Voltemos agora ao caso da TF do Dirac, temos que de acordo com (3-5.3)
TF[1] =  e-j2 e-j2 ftdt = ftdt =  (f ). (f ).
|
(3-6.5) |
mathend000#
Agora, como a função seno é impar o seu integral num intervalo simétrico é nulo, temos que
 (f )= 2 (f )= 2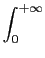 cos(2 cos(2 ft)dt. ft)dt.
|
(3-6.6) |
mathend000#
Estamos agora prontos para discutir o problema proposto, i.e.,
TF[u(t)] = 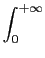 e-j2 e-j2 ftdt, ftdt,
|
(3-6.7) |
mathend000#
ou seja,
TF[u(t)] = 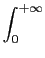 cos(2 cos(2 ft)dt - j ft)dt - j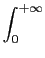 sin(2 sin(2 ft)dt, ft)dt,
|
(3-6.8) |
mathend000#
utilizando (3-6.6) no primeiro termo e (3-6.4) no segundo podemos escrever
TF[u(t)] = 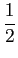  (f )- (f )- 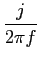 , ,
|
(3-6.9) |
mathend000#
que é o resultado pretendido.
Já agora, podemos determinar igualmente a relação recíproca da TF inversa do degrau na frequência, i.e.,
TFI[u(f )] =  u(f )ej2 u(f )ej2 ftdf. ftdf.
|
(3-6.10) |
mathend000#
Note-se que
U(f )= TF[u(t)]
mathend000# enquanto que u(f )
mathend000# é um degrau unitário em frequência, i.e., uma ``função'' que é igual a zero para f < 0
mathend000# e igual a um para f > 1
mathend000#. Podemos escrever
TFI[u(f )] = 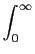 cos(2 cos(2 ft)df + j ft)df + j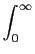 sin(2 sin(2 ft)df. ft)df.
|
(3-6.11) |
mathend000#
Utilizando o mesmo argumento de que a função seno é impar e portanto o seu integral entre
[- 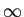 ,
,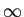 ]
mathend000# é zero, temos que de forma análoga ao caso da
TF[u(t)]
mathend000# mas revertendo de f
mathend000# para t
mathend000# que,
]
mathend000# é zero, temos que de forma análoga ao caso da
TF[u(t)]
mathend000# mas revertendo de f
mathend000# para t
mathend000# que,
 (t) = 2 (t) = 2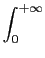 cos(2 cos(2 ft)df ft)df
|
(3-6.12) |
mathend000#
e que com a ajuda de (3-6.4) podemos escrever
TFI[u(f )] = 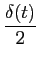 + + 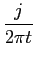 , ,
|
(3-6.13) |
mathend000#
que é o resultado procurado. Podemos agora obter versões equivalentes em  mathend000#, para a TF directa da função degrau unidade
mathend000#, para a TF directa da função degrau unidade
TF[u(t)] = 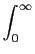 e-j e-j tdt = tdt =   ( ( ) - ) - 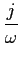 , ,
|
(3-6.14) |
mathend000#
onde 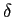 (f )
mathend000# foi substituido por
2
(f )
mathend000# foi substituido por
2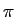
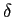 (
( )
mathend000# de acordo com (3-5.3) e para a TF inversa do degrau na frequência em
)
mathend000# de acordo com (3-5.3) e para a TF inversa do degrau na frequência em  mathend000#
mathend000#
TFI[u( )] )] |
= |
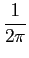 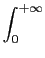 ej ej td td , , |
|
| |
= |
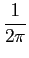 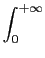 cos( cos( t)d t)d + + 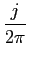 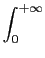 sin( sin( t)d t)d , , |
(3-6.15) |
onde utilizando (3-5.2) e que, mais uma vez, o integral da função sin
mathend000# é nulo num intervalo de
[- 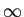 , +
, + 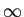 ]
mathend000# dando-nos o resultado do termo em cos
mathend000#
e que a partir de (3-6.4)
temos finalmente por substituição em (3-6.15) que
]
mathend000# dando-nos o resultado do termo em cos
mathend000#
e que a partir de (3-6.4)
temos finalmente por substituição em (3-6.15) que
A função ``sinal de'', ou sign em inglês, define-se por
sgn(t) = 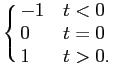
|
(3-7.01) |
mathend000#
Um forma simples de obter a TF de
sgn(t)
mathend000# é a de recordar que a função degrau unidade se pode escrever como
u(t) = 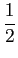 + + 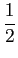 sgn(t), sgn(t),
|
(3-7.02) |
mathend000#
e tendo em conta (3-6.9) podemos concluir que
TF[sgn(t)] = 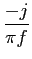 , ,
|
(3-7.03) |
mathend000#
ou de forma equivalente em  mathend000#, identificando com (3-6.14),
mathend000#, identificando com (3-6.14),
TF[sgn(t)] = 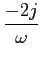 . .
|
(3-7.04) |
mathend000#
Como habitualmente vamos agora tratar o caso inverso, também interessante, da função sgn em frequência. Por analogia podemos escrever
u(f )= 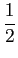 + + 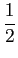 sgn(f ), sgn(f ),
|
(3-7.05) |
mathend000#
e mais uma vez, utilizando (3-6.13), temos que
TFI[sgn(f )] = 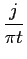 , ,
|
(3-7.06) |
mathend000#
ou o mesmo resultado em  mathend000#, tendo em conta (3-6.18).
mathend000#, tendo em conta (3-6.18).
No caso de um sinal periódico s(t)
mathend000#, de período T
mathend000#, representável por (F-0.6) e (F-0.7), a sua transformada de Fourier escreve-se
TF[s(t)] =  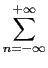 Cnejn2 Cnejn2 f0te-j2 f0te-j2 ftdt, ftdt,
|
(3-8.1) |
mathend000#
onde, invertendo o somatório e o integral,
TF[s(t)] = 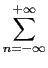 Cn Cn e-j2 e-j2 (f-nf0)tdt. (f-nf0)tdt.
|
(3-8.2) |
mathend000#
O integral representa simplesmente a TF[1] (3-5.3) no ponto f = nf0
mathend000# e portanto,
TF[s(t)] = 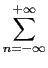 Cn Cn (f - nf0), (f - nf0),
|
(3-8.3) |
mathend000#
de onde se deduz que a TF de um sinal periódico, de período T = 1/f0
mathend000#, não é mais do que a repetição do espectro Cn
mathend000# com o período f0
mathend000#.
transformada de Fourier de
cos(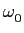 t)
mathend000#. Trata-se neste caso de uma função que não é limitada no tempo, cuja TF pode ser obtida facilmente com a ajuda do Dirac. Assim
t)
mathend000#. Trata-se neste caso de uma função que não é limitada no tempo, cuja TF pode ser obtida facilmente com a ajuda do Dirac. Assim
x(
t) = cos
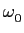 t
t =
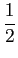 ej
ej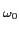 t
t +
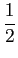 e-j
e-j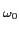 t
t,
mathend000#
e
mathend000#
utilizando (3-5.3) temos que
TF[
x(
t)] =

[

(

-
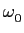
) +

(

+
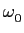
)],
mathend000#
o que indica que a energia da TF de x(t)
mathend000# está concentrada nas duas frequências - 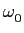 mathend000# e +
mathend000# e + 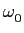 mathend000#.
mathend000#.
Transformada de Fourier de um ``pente'' de Diracs
É frequente necessitarmos o cálculo de
TF[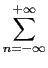  (t - nT0)], (t - nT0)],
|
(3-9.1) |
mathend000#
que é uma sucessão periódica, de período T0
mathend000#, de Diracs, vulgarmente chamada ``pente'' de Diracs ou simplesmente ``função pente''. Sabendo que (F-0.7) para o impulso de Dirac se escreve
Cn = 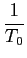 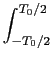  (t)e-jn (t)e-jn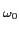 tdt = tdt = 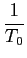 , ,
|
(3-9.2) |
mathend000#
temos que, por substituição em (3-8.3),
TF[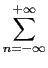  (t - nT0)] = f0 (t - nT0)] = f0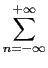  (f - nf0)], (f - nf0)],
|
(3-9.3) |
mathend000#
o que dá o interessante resultado que a TF de um ``pente'' de Diracs no tempo é ainda um ''pente'' de Diracs em frequência.
Processo de amostragem ideal: como aplicação interessante da TF do ``pente de Diracs'', podemos referir a representação do processo de amostragem ideal no domínio da frequência. Consideremos o sinal x(t)
mathend000# amostrado à taxa de amostragem de Ts
mathend000# segundos. O sinal amostrado escreve-se então, considerando a função de amostragem ideal, ou ``pente de Diracs'',
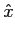 (t) (t) |
= |
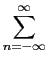 x(nTs) x(nTs) (t - nTs), (t - nTs), |
|
| |
= |
x(t) . s(t), |
(3-9.4) |
expressão já utilizada anteriormente e onde a função de amostragem ideal s(t)
mathend000# é dada por
s(t) = 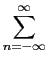  (t - nTs). (t - nTs).
|
(3-9.5) |
mathend000#
Calculemos agora a representação do sinal amostrado no domínio da frequência, calculdando
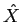 (f )= TF[
(f )= TF[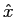 (t)]
mathend000#,
(t)]
mathend000#,
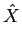 (f ) (f ) |
= |
 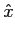 (t)e-j2 (t)e-j2 ftdt ftdt |
|
| |
= |
 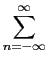 x(nTs) x(nTs) (t - nTs)e-j2 (t - nTs)e-j2 ftdt, ftdt, |
(3-9.6) |
invertendo a ordem entre o integral e o somatório e fazendo sair do integral as grandezas que não dependem do tempo t
mathend000#, temos
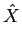 (f ) (f ) |
= |
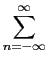 x(nTs) x(nTs)  (t - nTs)e-j2 (t - nTs)e-j2 ftdt, ftdt, |
|
| |
= |
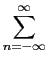 x(nTs) x(nTs)  ( ( )e-j2 )e-j2 f( f(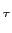 +nTs)d +nTs)d , , |
|
| |
= |
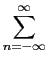 x(nTs)e-j2 x(nTs)e-j2 fnTs, fnTs, |
(3-9.7) |
visto que a
TF[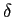 (t)] = 1
mathend000#. Esta expressão diz-nos simplesmente que a TF do sinal amostrado é igual à TF do sinal discreto no tempo definida em (3-3.5). Alternativamente, partindo de (3-9.4) podemos dizer que
(t)] = 1
mathend000#. Esta expressão diz-nos simplesmente que a TF do sinal amostrado é igual à TF do sinal discreto no tempo definida em (3-3.5). Alternativamente, partindo de (3-9.4) podemos dizer que
TF[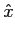 t)] t)] |
= |
TF[x(t) . s(t)] |
|
| |
= |
TF[x(t)] * TF[s(t)] |
|
| |
= |
X(f ) * fs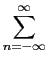  (f - nfs), (f - nfs), |
(3-9.8) |
de onde, em virtude da propriedade de sifting, temos que
TF[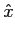 (t)] = fs (t)] = fs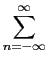 X(f - nfs), X(f - nfs),
|
(3-9.9) |
mathend000#
ou seja, a TF do sinal amostrado - igualmente a TF do sinal discreto no tempo - é uma repetição periódica (de período igual à frequência de amostragem fs
mathend000#) do espectro X(f )
mathend000# do sinal.
Já tivemos ocasião de referir que um sistema linear invariante no tempo pode ser representado por um sistema de equações diferenciais de coeficientes constantes do tipo (2-7.1). É útil, na análise de sistemas lineares, calcular a TF de ambos os membros da eq. (2-7.1)
utilizando recursivamente a propriedade da derivada podemos escrever a partir de (3-10.1)
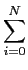 (- 1)i+1ai(j2 (- 1)i+1ai(j2 f )iY(f )= f )iY(f )= 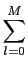 (- 1)l+1bl(j2 (- 1)l+1bl(j2 f )lX(f ), f )lX(f ),
|
(3-10.02) |
mathend000#
onde X(f )
mathend000# e Y(f )
mathend000# são as TF's de x(t)
mathend000# e y(t)
mathend000# respectivamente. Observando (3-10.2) pode-se constatar que através da TF as derivadas deixam lugar a simples multiplicações e que podemos reduzir a expressão que liga a TF de x(t)
mathend000# à TF de y(t)
mathend000# a
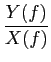 = = 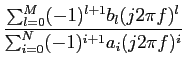 . .
|
(3-10.03) |
mathend000#
O segundo membro desta última equação é uma função de f
mathend000# à qual se chama função de transferência que se nota H(f )
mathend000# e que permite ligar a entrada e a saída do sistema através de
H(f )= 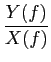 . .
|
(3-10.04) |
mathend000#
Dada a propriedade que permite afirmar que o produto de convolução no tempo é equivalente a um produto simples no domínio da frequência, podemos então dizer que a entrada x(t)
mathend000# e a saída y(t)
mathend000# de um sistema linear estão ligados entre si por uma relação de convolução através da resposta impulsiva h(t)
mathend000#, ou que
y(t) = x(t) * h(t)
mathend000#.
No caso da equação de diferenças (2-7.4) somos levados a utilizar a TF discreta no tempo, assim
TF{ aiy[n - i]} = TF{ aiy[n - i]} = TF{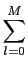 blx[n - l]}, blx[n - l]},
|
(3-10.05) |
mathend000#
ou ainda
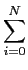 ai ai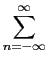 y[n - i]exp(-j2 y[n - i]exp(-j2 fn) = fn) = 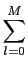 bl bl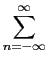 x[n - l]exp(-j2 x[n - l]exp(-j2 fn), fn),
|
(3-10.06) |
mathend000#
onde já foi invertida a ordem dos somatórios em i
mathend000# e l
mathend000# com os somatórios da TF em n
mathend000#. Fazendo agora uma mudança de variável k = n - i
mathend000# no primeiro membro e m = n - l
mathend000# no segundo, permite escrever
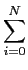 aiexp(-j2 aiexp(-j2 fi) fi) |
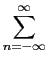 |
y[k]exp(-j2 fk) = fk) = |
|
| |
= 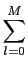 bl bl |
exp(-j2 fl ) fl )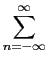 x[m]exp(-j2 x[m]exp(-j2 fm), fm), |
(3-10.07) |
e agora
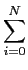 aiexp(-j2 aiexp(-j2 fi)Y(f )= fi)Y(f )= 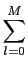 blexp(-j2 blexp(-j2 fl )X(f ), fl )X(f ),
|
(3-10.08) |
mathend000#
e, como no caso contínuo,
H(f )= 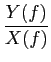 = = 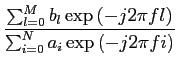 . .
|
(3-10.09) |
mathend000#
Veremos mais tarde que a definição de um novo espaço de variável
z = ej2 f
mathend000#, permite definir uma nova transformada, denominada Transformada em Z (TZ)
f
mathend000#, permite definir uma nova transformada, denominada Transformada em Z (TZ)
TZ{y[n]} = 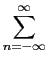 y[n]z-nT, y[n]z-nT,
|
(3-10.10) |
mathend000#
onde frequentemente T = 1
mathend000#. A partir de (3-10.9) podemos escrever directamente a TZ de h[n]
mathend000# como
H(z) = 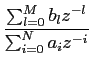 . .
|
(3-10.11) |
mathend000#
Neste equação podemos notar que tanto o denominador como o numerador da fração são polinómios em z. As raízes do denominador, chamados pólos, são muito importantes para a determinação da estabilidade do sistema. As raízes do numerador são chamados os zeros do sistema.
calcular o espectro de potência normalizado da função
g(t) = 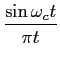 . .
|
(3-10.12) |
mathend000#
A potência normalizada é a potência dissipada numa resistência de 1 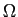 mathend000#. Trata-se portanto de calcular o espectro de
f (t) = g2(t)
mathend000# que não é mais do que a TF dum produto temporal g(t)g(t)
mathend000#. Portanto
mathend000#. Trata-se portanto de calcular o espectro de
f (t) = g2(t)
mathend000# que não é mais do que a TF dum produto temporal g(t)g(t)
mathend000#. Portanto
F( ) = ) = 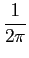 G( G( ) * G( ) * G( ), ),
|
(3-10.13) |
mathend000#
usando a TF da função
(sin x)/x
mathend000#,
G( ) = rect( ) = rect(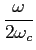 ), ),
|
(3-10.14) |
mathend000#
o integral de convolução torna-se numa convolução de duas funções rectangulares obtendo-se evidentemente uma função triangular da forma
calcular o espectro da função f (t)
mathend000# formada pela série de Diracs definida por
f (t) = 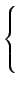 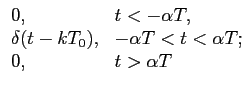
|
(3-10.16) |
mathend000#
Comecemos por considerar a seguinte série infinita de Diracs,
g(t) = 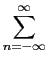  (t - nT0), (t - nT0),
|
(3-10.17) |
mathend000#
da qual se conhece a transformada de Fourier que não é outra senão uma série de Diracs em frequência,
G( ) = ) = 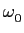 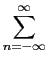  ( ( - n - n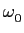 ), com ), com 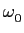 = 2 = 2 /T0 /T0
|
(3-10.18) |
mathend000#
Agora podemos multiplicar a função temporal g(t)
mathend000# por uma janela rectangular de tal modo a obter
f (t) = m(t)g(t)
mathend000#,
![]() t
t
![]()
![]() e
e![]() te-stdt,
te-stdt,
![]()
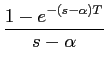 ,
,
![]()
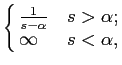
![]() =
= ![]()
![]() =
= 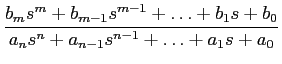 .
.
![\includegraphics[width=8cm]{figs/fig4-5.eps}](img159.png)
![]() tu(t)
tu(t)
![]() e-
e-![]() te-stdt =
te-stdt = ![]()
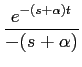
![]() =
= 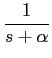 ,
,
![]()
![]() e-(s+2)tdt +
e-(s+2)tdt + ![]() e-(s+4)tdt,
e-(s+4)tdt,
![]()
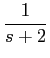 +
+ 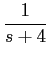 = 2
= 2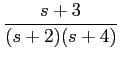 ,
,
![]() t)u(t)
t)u(t)
![]() cos(
cos(![]() t)e-stdt
t)e-stdt
![]()
![]() e-(s+j
e-(s+j![]() )tdt +
)tdt + ![]()
![]() e-(s-j
e-(s-j![]() )tdt
)tdt
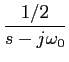 +
+ 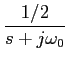 =
= 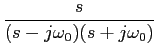 ,
,
![]() f (t - t0)e-stdt,
f (t - t0)e-stdt,
![]() = t - t0
= t - t0
![]() = dt
= dt
![]() f (
f (![]() )e-s(t0+
)e-s(t0+![]() )d
)d![]() ,
,
![]() f (t)e-stdt,
f (t)e-stdt,
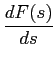 =
= ![]() [- tf (t)]e-stdt,
[- tf (t)]e-stdt,
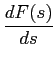 ,
,
![]() ,
,
![]() .
.
![]()
![]()
![]() = sF(s) - f (0-),
= sF(s) - f (0-),
![]()
![]()
![]() =
= ![]()
![]() e-stdt,
e-stdt,
![]() -
- ![]() f (t)[- se-st], dt
f (t)[- se-st], dt
![]()
![]() f (
f (![]() )d
)d![]() ,
,
![]() = t -
= t - ![]()
![]() f (t - kT),
f (t - kT),
![]() e-kTs
e-kTs
![]() f (t - kT)
f (t - kT)
![]() f (t - kT) -
f (t - kT) - 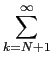 f (t - kT),
f (t - kT),
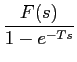 -
- 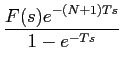
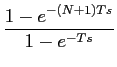 F(s).
F(s).
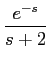 ,
,
![]()
![]() (t - 1)e-stdt = e-s,
(t - 1)e-stdt = e-s,
![]() e-2te-stdt =
e-2te-stdt = 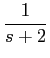 ,
,
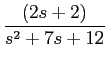 ,
,
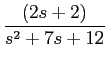 =
= 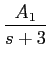 +
+ 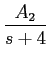 ,
,
![]() aifi(t)] =
aifi(t)] = ![]() aiFi(s),
aiFi(s),
![]() + by = x(t),
+ by = x(t),
![]() ,
,
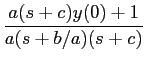 ,
,
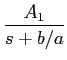 +
+ ![]() ,
,
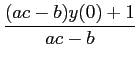 A2 =
A2 = 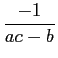 ,
,
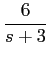 ,
,
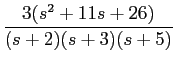 =
= 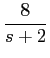 -
- 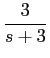 -
- 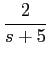 ,
,
![]()
![]() + x -
+ x - ![]()
![]() = f (t) = 2u(t)
= f (t) = 2u(t)
![]()
![]() +
+ ![]()
![]() + y = 0,
+ y = 0,
![]() s + 1)X(s) -
s + 1)X(s) - ![]() sY(s) = F(s) =
sY(s) = F(s) = ![]()
![]() sX(s) + (
sX(s) + (![]() s + 1)Y(s) = 0,
s + 1)Y(s) = 0,
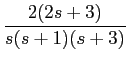 =
= ![]() -
- 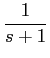 -
- 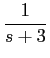
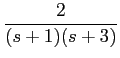 =
= 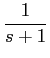 -
- 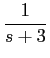 ,
,
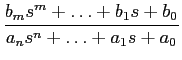 X(s).
X(s).
![]() =
= 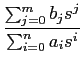 .
.
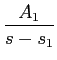 +
+ 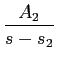 +...+
+...+ 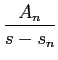 ,
,
![]() (t)] = 1
(t)] = 1
![]() + y(t),
+ y(t),
![]() =
= 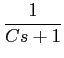 .
.
![]() e-t/Cu(t),
e-t/Cu(t),
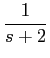 ,
,
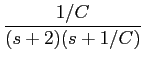 =
= 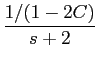 +
+ 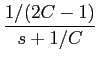 ,
,
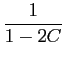 e-2t +
e-2t + 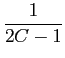 e-t/C]u(t),
e-t/C]u(t),
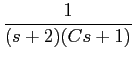 +
+ 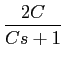 ,
,
![]()
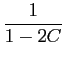 e-2t +
e-2t + 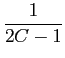 e-t/C +2e-t/C
e-t/C +2e-t/C![]() u(t),
u(t),
![]()
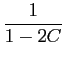 e-2t +
e-2t + 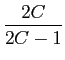 e-t/C
e-t/C![]() u(t).
u(t).
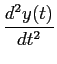 +2
+2![]() +2y(t) = 2
+2y(t) = 2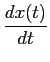 + 2x(t),
+ 2x(t),
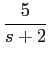 ,
,
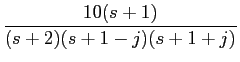 ,
,
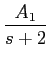 +
+ 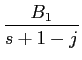 +
+ 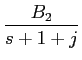 ,
,
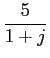 ,
,
![]() e
e![]() ,
,
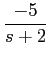 +
+ ![]()
![]()
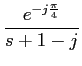 +
+ 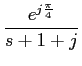
![]() .
.
![]() [
[![]() e(-1+j)t +
e(-1+j)t + ![]() e(-1-j)t]u(t),
e(-1-j)t]u(t),
![]() e-t[e
e-t[e![]() + e
+ e![]() ]u(t),
]u(t),
![]() e-tcos(t -
e-tcos(t - ![]() ) - 5e-2t]u(t).
) - 5e-2t]u(t).
![]() )
)
![]() )
)
![]() )|
)|
![]() )
)
![]() /2
/2![]()
![]() nT
nT
![]()
![]() +2
+2![]() /T
/T
![]() +
+ ![]() )
)![]() s(nT)e
s(nT)e![]()
![]() s(nT)e-j
s(nT)e-j![]() nT-2
nT-2![]() n
n![]() s(nT)e-j(
s(nT)e-j(![]() nT)
nT)![]() ),
),![]() n) = 1
n) = 1
![]() /T
/T
![]() ) =
) = ![]() [fR(t)cos
[fR(t)cos![]() t + fX(t)sin
t + fX(t)sin![]() t]dt,
t]dt,
![]() ) = -
) = - ![]() [fR(t)sin
[fR(t)sin![]() t - fX(t)cos
t - fX(t)cos![]() t]dt,
t]dt,
![]() ) = R(
) = R(![]() ) + jX(
) + jX(![]() )
)
![]()
![]() [R(
[R(![]() )cos
)cos![]() t - X(
t - X(![]() )sin
)sin![]() t]d
t]d![]() ,
,
![]()
![]() [R(
[R(![]() )sin
)sin![]() t + X(
t + X(![]() )cos
)cos![]() t]d
t]d![]() .
.
![]() ) =
) = ![]() f (t)cos
f (t)cos![]() tdt
tdt
![]() ) = -
) = - ![]() f (t)sin
f (t)sin![]() tdt
tdt
![]() ) = R(-
) = R(- ![]() )
)
![]() ) = - X(-
) = - X(- ![]() )
)
![]() ) = F * (
) = F * (![]() )
)
![]() ) = F * (
) = F * (![]() )
)
![]() ) =
) = ![]() f (t)cos
f (t)cos![]() tdt = 2
tdt = 2![]() f (t)cos(
f (t)cos(![]() t)dt,
t)dt,
![]() ) = 0,
) = 0,
![]() ) = 0,
) = 0,
![]() ) = - 2
) = - 2![]() f (t)sin
f (t)sin![]() tdt.
tdt.
![]()
![]() x1(t -
x1(t - ![]() )x2(
)x2(![]() )d
)d![]() e-j2
e-j2![]() ftdt,
ftdt,
![]()
![]()
![]() x1(v)x2(
x1(v)x2(![]() )e-j2
)e-j2![]() f(v+
f(v+![]() )d
)d![]() dv,
dv,
![]() [
[![]() x1(v)e-j2
x1(v)e-j2![]() fvdv]x2(
fvdv]x2(![]() )e-j2
)e-j2![]() f
f![]() d
d![]() ,
,
![]()
![]()
![]()
![]() , 0]
, 0]
![]() ]
]
![]() [
[![]() X1(v)ej2
X1(v)ej2![]() vtdv]x2(t)e-j2
vtdv]x2(t)e-j2![]() ftdt
ftdt![]() X1(v)
X1(v)![]() x2(t)e-j2
x2(t)e-j2![]() (f-v)tdtdv
(f-v)tdtdv![]() X1(v)X(f - v)dv
X1(v)X(f - v)dv![]()
![]() )X2(
)X2(![]() ),
),
![]() X1(
X1(![]() ) * X2(
) * X2(![]() ).
).
![]() rect(
rect(![]() ) =
) = ![]()
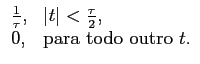
![]() rect(
rect(![]() )]
)]![]()
![]() e-j
e-j![]() tdt
tdt![]() [
[![]() ]-
]-![]() /2
/2![]() /2,
/2,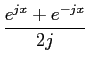 ,
,
![]() rect(
rect(![]() )]
)]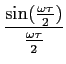
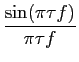
![]() f )
f )![]() )] =
)] = ![]() sinc(
sinc(![]() f ),
f ),
![]() f )] =
f )] = ![]() rect(
rect(![]() ).
).
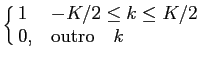
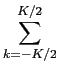 e-j2
e-j2![]() fkT,
fkT,
![]() e-j2
e-j2![]() f(n-K/2)T,
f(n-K/2)T,![]() fKT
fKT![]() e-j2
e-j2![]() fnT,
fnT,![]() fT
fT
![]() fKT
fKT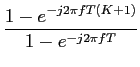 ,
,
![]() fT)
fT)
![]() fT)
fT)
![\includegraphics[width=10cm]{figs/TF_plots2.eps}](img302.png)
![]() )] =
)] = ![]() rect(
rect(![]() f ),
f ),
![]() f )] =
f )] = ![]() sinc(
sinc(![]() ).
).
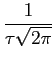 e
e![]() .
.
![]() ) =
) = ![]() g(t)e-j
g(t)e-j![]() tdt =
tdt = ![]()
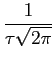 e
e![]() e-j
e-j![]() tdt,
tdt,
![]() (t2 +2
(t2 +2![]() j
j![]() t),
t),
![]()
![]()
![]() (t + j
(t + j![]()
![]() )2 -
)2 - ![]() .
.
![]() e-ax2dx =
e-ax2dx = ![]()
![]() ,
,
![]() ) = e
) = e![]() ,
,
![]() (t)
(t)
![]() (
(![]() )
)
![]()
![]()
![]() (t)] =
(t)] = ![]()
![]() (t)e-j2
(t)e-j2![]() ftdt = e-j2
ftdt = e-j2![]() f0 = 1
f0 = 1
![]() 1ej2
1ej2![]() ftdf
ftdf![]() (t).
(t).![]() 1e-j2
1e-j2![]() ftdt
ftdt![]() (f ),
(f ),![]() (f )]
(f )]![]()
![]() (f )ej2
(f )ej2![]() ftdf
ftdf![]() g(t)dt =
g(t)dt = ![]()
![]() g(t)e-b|t|dt,
g(t)e-b|t|dt,
![]() sin(at)dt,
sin(at)dt,
![]() sin(at)dt
sin(at)dt![]()
![]() sin(at)e-btdt
sin(at)e-btdt![]()
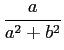
![]()
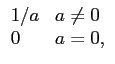
![]() e-j2
e-j2![]() ftdt =
ftdt = ![]() (f ).
(f ).
![]() e-j2
e-j2![]() ftdt,
ftdt,
![]() cos(2
cos(2![]() ft)dt - j
ft)dt - j![]() sin(2
sin(2![]() ft)dt,
ft)dt,
![]() u(f )ej2
u(f )ej2![]() ftdf.
ftdf.
![]() cos(2
cos(2![]() ft)df + j
ft)df + j![]() sin(2
sin(2![]() ft)df.
ft)df.
![]() ,
,![]() ]
]
![]()
![]() (f )
(f )
![]()
![]() (
(![]() )
)
![]()
![]() , +
, + ![]() ]
]
![]() cos(
cos(![]() t)d
t)d![]() =
= ![]()
![]() (t),
(t),
![]() sin(
sin(![]() t)d
t)d![]() =
= ![]() ,
,
![]() +
+ ![]() sgn(t),
sgn(t),
![]()
![]() +
+ ![]() sgn(f ),
sgn(f ),
![]()
![]()
![]() Cnejn2
Cnejn2![]() f0te-j2
f0te-j2![]() ftdt,
ftdt,
![]() Cn
Cn![]() e-j2
e-j2![]() (f-nf0)tdt.
(f-nf0)tdt.
![]() t)
t)
![]() t =
t = ![]() ej
ej![]() t +
t + ![]() e-j
e-j![]() t,
t,
![]()
![]() e-j(
e-j(![]() -
-![]() )tdt +
)tdt + ![]()
![]() e-j(
e-j(![]() +
+![]() )tdt,
)tdt,
![]() [
[![]() (
(![]() -
- ![]() ) +
) + ![]() (
(![]() +
+ ![]() )],
)],
![]()
![]()
![]()
![]() (t - nT0)],
(t - nT0)],
![]()
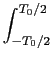
![]() (t)e-jn
(t)e-jn![]() tdt =
tdt = ![]() ,
,
![]()
![]() (t - nTs).
(t - nTs).
![]() (f )= TF[
(f )= TF[![]() (t)]
(t)]
![]() (f )
(f )![]()
![]() (t)e-j2
(t)e-j2![]() ftdt
ftdt![]()
![]() x(nTs)
x(nTs)![]() (t - nTs)e-j2
(t - nTs)e-j2![]() ftdt,
ftdt,![]() (f )
(f )![]() x(nTs)
x(nTs)![]()
![]() (t - nTs)e-j2
(t - nTs)e-j2![]() ftdt,
ftdt,![]() x(nTs)
x(nTs)![]()
![]() (
(![]() )e-j2
)e-j2![]() f(
f(![]() +nTs)d
+nTs)d![]() ,
,![]() x(nTs)e-j2
x(nTs)e-j2![]() fnTs,
fnTs,![]() (t)] = 1
(t)] = 1
![]() t)]
t)]![]()
![]() (f - nfs),
(f - nfs),![]() (t)] = fs
(t)] = fs![]() X(f - nfs),
X(f - nfs),
![]() aiy[n - i]} = TF{
aiy[n - i]} = TF{![]() blx[n - l]},
blx[n - l]},
![]() ai
ai![]() y[n - i]exp(-j2
y[n - i]exp(-j2![]() fn) =
fn) = ![]() bl
bl![]() x[n - l]exp(-j2
x[n - l]exp(-j2![]() fn),
fn),
![]() aiexp(-j2
aiexp(-j2![]() fi)
fi)![]()
![]() fk) =
fk) =![]() bl
bl![]() fl )
fl )![]() x[m]exp(-j2
x[m]exp(-j2![]() fm),
fm),![]() aiexp(-j2
aiexp(-j2![]() fi)Y(f )=
fi)Y(f )= ![]() blexp(-j2
blexp(-j2![]() fl )X(f ),
fl )X(f ),
![]() f
f
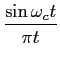 .
.
![]()
![]() ) =
) = ![]() G(
G(![]() ) * G(
) * G(![]() ),
),
![]() ) = rect(
) = rect(![]() ),
),
![]() ) =
) = ![]()
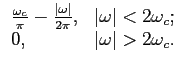
![]()
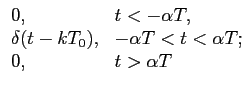
![]()
![]() (t - nT0),
(t - nT0),
![]() ) =
) = ![]()
![]()
![]() (
(![]() - n
- n![]() ), com
), com ![]() = 2
= 2![]() /T0
/T0
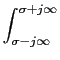 F(s)estds,
F(s)estds,
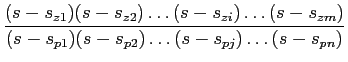 ,
,
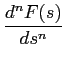 .
.
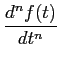
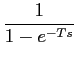
![\includegraphics[width=8cm]{figs/fig4-6.eps}](img238.png)
![\includegraphics[width=10cm]{figs/fig4-7.eps}](img253.png)
![\includegraphics[width=8cm]{figs/fig4-8.eps}](img274.png)
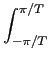 S(
S(![\includegraphics[width=10cm]{figs/TF_plots1.eps}](img293.png)
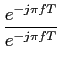
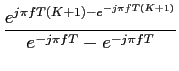 ,
,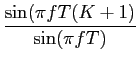 ,
,![$\displaystyle {{{\rm sinc} [fT(K+1)]}\over {{\rm sinc} (fT)}}$](img301.png) ,
,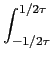 ej2
ej2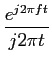
![$\displaystyle \left.\vphantom{{{e^{j2\pi ft}}\over {j2\pi t}}}\right]_{{-1/2\tau}}^{{1/2\tau}}$](img306.png)
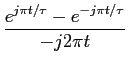
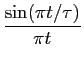
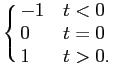
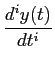
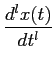
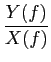 =
= 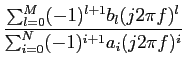 .
.
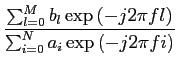 .
.
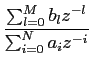 .
.