mathend000# representada na figura F.1.
truemm
Figura F.1:
onda quadrada.
|
![\includegraphics[height=60mm]{figs/onda-quadrada.ps}](img645.png) |
Observando o sinal da figura F.1 podemos desde já
determinar
que a0 = 0
mathend000# pois este coeficiente é proporcional ao valor médio
do sinal que neste caso é nulo. Por outro lado, visto que o
sinal representado é uma função par, temos que o
desenvolvimento em série deverá ser também uma função
par e que portanto bn = 0
mathend000#. Calculemos então an
mathend000#. Utilizando
F-0.3
an = -
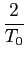
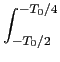
cos
n tdt
tdt +
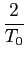
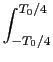
cos
n tdt
tdt -
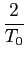
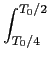
cos
n tdt
tdt,
mathend000#
com T0 = 2
mathend000#. Integrando o coseno nos devidos intervalos e pondo em factor
1/n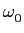 mathend000# obtem-se
mathend000# obtem-se
an = -
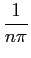
[- sin(
n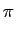
/2) + sin(
n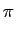
) - sin(
n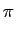
/2) - sin(
n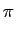
/2) + sin(
n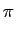
) - sin(
n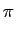
/2)],
mathend000#
sabendo que
sin n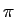 = 0
mathend000# e juntando os termos em
sin(n
= 0
mathend000# e juntando os termos em
sin(n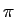 /2)
mathend000#
/2)
mathend000#
an =
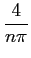
sin
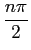
.
mathend000#
O desenvolvimento de s(t)
mathend000# escreve-se então
s(
t) =
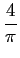
(cos
 t
t -
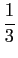
cos 3
 t
t +
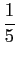
cos 5
 t
t +...+
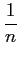
sin
n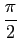
cos
n t
t +...),
mathend000#
com
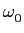 = 2
= 2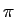 /T0 =
/T0 = 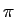 mathend000#.
mathend000#.
truemm
Figura F.2:
sinal sinusoidal.
|
![\includegraphics[height=60mm]{figs/sinusoide.ps}](img656.png) |
calcular o desenvolvimento em série de Fourier
da onda sinusoidal, de valor médio nulo, periódica, de período
T0
mathend000# e amplitude unidade representada na figura F.2.
Como no exemplo anterior, trata-se de um sinal par, de valor
médio nulo e portanto a0 = bn = 0
mathend000#. Assim
mathend000#
com T0 = 2
mathend000#. Sabendo que
cos a cos b = 1/2[cos(a + b) + cos(a - b)]
mathend000#
(ver anexo) obtemos fácilmente, após integração,
an =
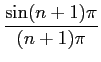
+
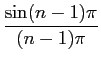
,
mathend000#
ou numa forma mais compacta
an =
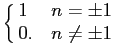
mathend000#
Utilizando F-0.2 obtemos (como aliás seria evidente
desde o início)
s(
t) = cos
 t
t.
mathend000#
O coeficiente Cn
mathend000# da equação F-0.7 é uma função
de ordem n
mathend000# da variável discreta n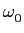 mathend000# (harmónica n
mathend000# de s(t)
mathend000#)
e dá uma representação (discreta) do sinal s(t)
mathend000# no
domínio da frequência. Por essa razão é geralmente chamado
espectro do sinal
periódico s(t)
mathend000#. Cn
mathend000# é em geral uma função complexa
e contém, nesse caso, a informação de amplitude e de fase
das componentes (harmónicas) de s(t)
mathend000# que se pode escrever sob
a forma
mathend000# (harmónica n
mathend000# de s(t)
mathend000#)
e dá uma representação (discreta) do sinal s(t)
mathend000# no
domínio da frequência. Por essa razão é geralmente chamado
espectro do sinal
periódico s(t)
mathend000#. Cn
mathend000# é em geral uma função complexa
e contém, nesse caso, a informação de amplitude e de fase
das componentes (harmónicas) de s(t)
mathend000# que se pode escrever sob
a forma
Cn(n ) = ) =  Cn(n Cn(n ) ) ej ej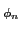 (n (n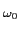 ), ),
|
(F.-0.08) |
mathend000#
onde
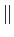 Cn(n
Cn(n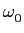 )
)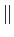 mathend000# é o espectro de amplitude e
mathend000# é o espectro de amplitude e
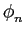 (n
(n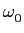 )
mathend000# é o espectro de fase de s(t)
mathend000#.
)
mathend000# é o espectro de fase de s(t)
mathend000#.
demonstrar que
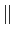 Cn(n Cn(n ) )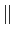 = = 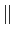 C-n(- n C-n(- n ) )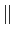 = = 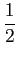 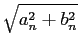 = = 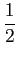 An, An,
|
(F.-0.09) |
mathend000#
e que
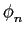 (n (n ) = arctan(- ) = arctan(- 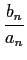 ) = ) = 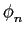 , ,
|
(F.-0.10) |
mathend000#
e
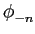 (n (n ) = arctan( ) = arctan(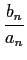 ) = - ) = - 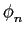 . .
|
(F.-0.11) |
mathend000#
calcular o espectro
Cn(n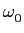 )
mathend000# da onda quadrada
da figura F.1. Verificar o resultado utilizando as
relações entre Cn
mathend000#, an
mathend000# e bn
mathend000#.
)
mathend000# da onda quadrada
da figura F.1. Verificar o resultado utilizando as
relações entre Cn
mathend000#, an
mathend000# e bn
mathend000#.
Para a onda quadrada da figura F.1
mathend000#
Integrando a exponencial nos mesmos intervalos que no
exercício anterior obtemos
Cn(
n
) = -
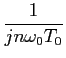
[2
e-jn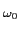 T0/4
T0/4 -2
ejn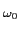 T0/4
T0/4 +
ejn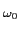 T0/2
T0/2 -
e-jn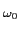 T0/2
T0/2],
mathend000#
utilizando a conhecida forma
sin x = (1/2j)(ejx - e-jx)
mathend000# obtemos
a partir da relação anterior
Cn(
n
) =
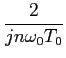
[2
j sin(
n T0
T0/4)] -
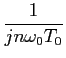
[2
j sin(
n T0
T0/2)];
mathend000#
simplificando por j
mathend000# e sabendo que o segundo termo é nulo temos que
mathend000#
A figura F.3 mostra uma representação gráfica
de
Cn(n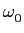 )
mathend000# para
-10 < n < 10
mathend000#.
)
mathend000# para
-10 < n < 10
mathend000#.
truemm
Figura F.3:
espectro de amplitude discreto Cn
mathend000#.
|
![\includegraphics[height=60mm]{figs/espectro-Cn.ps}](img670.png) |
Utilizando os valores de an
mathend000# e bn
mathend000# do exercício anterior e sabendo que
|Cn|= 1/2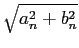 mathend000# e que
mathend000# e que
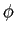 (n
(n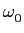 ) =
) = 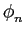 = 0
mathend000#
obtem-se fácilmente o resultado acima.
= 0
mathend000#
obtem-se fácilmente o resultado acima.
calcular o espectro
Cn(n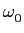 )
mathend000# do sinal da
figura F.2. Aplicando a forma geral
)
mathend000# do sinal da
figura F.2. Aplicando a forma geral
mathend000#
Utilizando a forma exponencial do coseno,
Cn(
n
) =
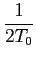
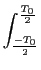 ej
ej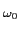 t(1-n)
t(1-n) +
e-j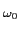 t(1+n)dt
t(1+n)dt,
mathend000#
integrando no devido intervalo e voltando a substituir a forma exponencial
da função seno
Cn(
n
) =
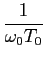
[
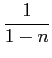
sin[

(1 -
n)
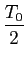
] +
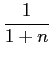
sin[

(1 +
n)
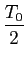
]];
mathend000#
pondo sob a forma habitual de sin x/x
mathend000#,
mathend000#
esta função é sempre nula para qualquer valor de n
mathend000# salvo para
n = - 1
mathend000# e n = 1
mathend000# onde toma o valor 1/2. Podemos então desenhar o seu
espectro de amplitude
Figura F.4:
espectro de amplitude discreto Cn
mathend000# de uma sinusoide.
|
![\includegraphics[height=60mm]{figs/espectro-sin.ps}](img681.png) |
Sergio Jesus
2008-12-30
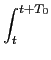 |s(u)|du <
|s(u)|du < 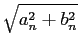 ,
,
![]()
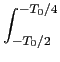 cos n
cos n![]() tdt +
tdt + ![]()
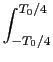 cos n
cos n![]() tdt -
tdt - ![]()
![]() cos n
cos n![]() tdt,
tdt,
![]()
![]() [- sin(n
[- sin(n![]() /2) + sin(n
/2) + sin(n![]() ) - sin(n
) - sin(n![]() /2) - sin(n
/2) - sin(n![]() /2) + sin(n
/2) + sin(n![]() ) - sin(n
) - sin(n![]() /2)],
/2)],
![]() = 0
= 0
![]() /2)
/2)
![]() sin
sin![]() .
.
![]() (cos
(cos![]() t -
t - ![]() cos 3
cos 3![]() t +
t + ![]() cos 5
cos 5![]() t +...+
t +...+ ![]() sin n
sin n![]() cos n
cos n![]() t +...),
t +...),
![]() = 2
= 2![]() /T0 =
/T0 = ![]()
![]()
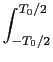 cos
cos![]() t cos n
t cos n![]() tdt,
tdt,
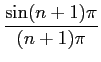 +
+ 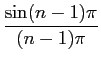 ,
,
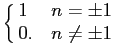
![]() t.
t.
![]()
![]() ) =
) = ![]() Cn(n
Cn(n![]() )
)![]() ej
ej![]() (n
(n![]() ),
),
![]() Cn(n
Cn(n![]() )
)![]()
![]() (n
(n![]() )
)
![]() Cn(n
Cn(n![]() )
)![]() =
= ![]() C-n(- n
C-n(- n![]() )
)![]() =
= ![]()
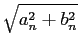 =
= ![]() An,
An,
![]() (n
(n![]() ) = arctan(-
) = arctan(- ![]() ) =
) = ![]() ,
,
![]() (n
(n![]() ) = arctan(
) = arctan(![]() ) = -
) = - ![]() .
.
![]() )
)
![]() ) =
) = ![]()
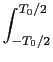 s(t)e-jn
s(t)e-jn![]() tdt.
tdt.
![]() ) = -
) = - 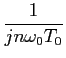 [2e-jn
[2e-jn![]() T0/4 -2ejn
T0/4 -2ejn![]() T0/4 + ejn
T0/4 + ejn![]() T0/2 - e-jn
T0/2 - e-jn![]() T0/2],
T0/2],
![]() ) =
) = 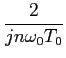 [2j sin(n
[2j sin(n![]() T0/4)] -
T0/4)] - 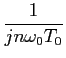 [2j sin(n
[2j sin(n![]() T0/2)];
T0/2)];
![]() ) =
) = 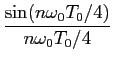 =
= 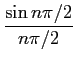 .
.
![]() )
)
![]()
![]() (n
(n![]() ) =
) = ![]() = 0
= 0
![]() )
)
![]() ) =
) = ![]()
![]() cos(
cos(![]() t)e-jn
t)e-jn![]() tdt.
tdt.
![]() ) =
) = ![]()
![]() ej
ej![]() t(1-n) + e-j
t(1-n) + e-j![]() t(1+n)dt,
t(1+n)dt,
![]() ) =
) = ![]() [
[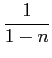 sin[
sin[![]() (1 - n)
(1 - n)![]() ] +
] + 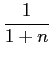 sin[
sin[![]() (1 + n)
(1 + n)![]() ]];
]];
![]() ) =
) = ![]()
![$\displaystyle {{\sin [\omega_0 (1-n){T_0\over 2}]}\over
{\omega_0(1-n){T_0\over 2}}}$](img678.png) +
+ ![]()
![$\displaystyle {{\sin [\omega_0 (1+n){T_0\over 2}]}\over
{\omega_0(1+n){T_0\over 2}}}$](img679.png) =
= ![]()
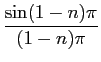 +
+ ![]()
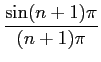 ,
,