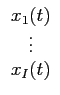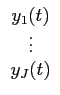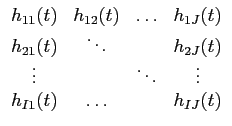Subsecções
Sistemas lineares invariantes no tempo (SLIT)
Espaços de entrada e espaços de saída
Acabámos de referir na introdução que o conceito de sinal se encontra ligado às observações que fazemos da natureza que nos rodeia. Um dos objectivos essenciais é o de retirar destas observações, ou sinais, a informação que nos interessa.
Essa operação de extração da informação é normalmente feita através da passagem do sinal através de um operador ou sistema que pelo seu lado produz um resultado. Portanto o operador ou sistema transforma o sinal (ou sinais) de entrada no sinal (ou sinais) de saída.
Neste capítulo vamos supôr que tanto os sinais de entrada como os sinais de saída pertencem a um conjunto fechado em relação à adição e à multiplicação por um escalar. Isto significa que se adicionarmos dois sinais do conjunto, eventualmente multiplicados por escalares, obtemos ainda um sinal resultante pertencente ao mesmo conjunto. Este é chamado um espaço linear.
Sinais contínuos e sinais discretos
Um sinal contínuo x(t)
mathend000# de variável real t
mathend000#, possui um número infinito de valores num intervalo de tempo
t  [a, b]
mathend000#. Como tal torna-se impossível a sua análise e processamento por calculadores númericos pelo que, se torna necessário proceder à sua amostragem, sendo a versão amostrada
[a, b]
mathend000#. Como tal torna-se impossível a sua análise e processamento por calculadores númericos pelo que, se torna necessário proceder à sua amostragem, sendo a versão amostrada
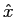 (t)
mathend000#
(t)
mathend000#
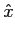 (t) = (t) = 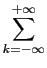 x(kT)p(t - kT), x(kT)p(t - kT),
|
(2-2.01) |
mathend000#
onde x(kT)
mathend000# representa a amplitude do sinal x
mathend000# no ponto kT
mathend000#, k
mathend000# é um número inteiro k 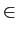 Z
mathend000#, p(t)
mathend000# é uma ``função'' infinitamente estreita no ponto t = 0
mathend000# e zero para t
Z
mathend000#, p(t)
mathend000# é uma ``função'' infinitamente estreita no ponto t = 0
mathend000# e zero para t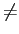 0
mathend000# (como por exemplo o Dirac) e T
mathend000# é o intervalo de amostragem. Mediante certas condições sobre o sinal p(t)
mathend000# e o intervalo de amostragem T
mathend000#, o sinal x(t)
mathend000# pode ser substituido pelo conjunto de amostras x(kT)
mathend000#. Assim se o sinal x(t)
mathend000# tomar um número infinito de valores no intervalo
t
0
mathend000# (como por exemplo o Dirac) e T
mathend000# é o intervalo de amostragem. Mediante certas condições sobre o sinal p(t)
mathend000# e o intervalo de amostragem T
mathend000#, o sinal x(t)
mathend000# pode ser substituido pelo conjunto de amostras x(kT)
mathend000#. Assim se o sinal x(t)
mathend000# tomar um número infinito de valores no intervalo
t 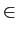 [a, b]
mathend000#, x(kT)
mathend000# tomará igualmente um número finito de valores para
ka,
[a, b]
mathend000#, x(kT)
mathend000# tomará igualmente um número finito de valores para
ka,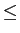 k
k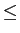 kb
mathend000#, onde
ka = int[a/T]
mathend000# e
kb = int[b/T] + 1
mathend000#. Por vezes, para simplificar a notação, o sinal discreto x(kT)
mathend000# escreve-se apenas x(k)
mathend000#, xk
mathend000# ou ainda x[k]
mathend000#. Normalmente sinais digitais são sinais discretos cuja amplitude foi também discretizada. Por abuso de linguagem, utilizaremos indiferenciadamente a denominação sinais digitais e sinais discretos.
kb
mathend000#, onde
ka = int[a/T]
mathend000# e
kb = int[b/T] + 1
mathend000#. Por vezes, para simplificar a notação, o sinal discreto x(kT)
mathend000# escreve-se apenas x(k)
mathend000#, xk
mathend000# ou ainda x[k]
mathend000#. Normalmente sinais digitais são sinais discretos cuja amplitude foi também discretizada. Por abuso de linguagem, utilizaremos indiferenciadamente a denominação sinais digitais e sinais discretos.
Excitações e respostas de sistemas LIT
De acordo com o que foi dito, relativamente aos espaços de entrada e de saída, um sistema estável transformará um sinal do espaço de entrada num sinal do espaço de saída. Vamos por enquanto adoptar uma representação de um sinal sob forma de uma função contínua, real e de variável real, que é o tempo t
mathend000#. Assim podemos simplesmente dizer que o sinal de entrada x(t)
mathend000# se transforma no sinal de saída y(t)
mathend000# através da transformação L
mathend000# tal que
A transformação L é dita invariante no tempo se, e só se, o modo como opera no espaço de entrada não se altera por translação temporal, assim
L[x(t - t0)] = y(t - t0), 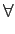 t0. t0.
|
(2-3.02) |
mathend000#
A transformação L é linear se e só se
| L[ax1(t) + bx2(t)] |
= |
aL[x1(t)] + bL[x2(t)] |
|
| |
= |
ay1(t) + by2(t). |
(2-3.03) |
Podemos agora generalizar sob forma de combinação linear
L[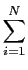 aixi(t)] aixi(t)] |
= |
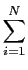 aiL[xi(t)] aiL[xi(t)] |
|
| |
= |
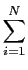 aiyi(t), aiyi(t), |
(2-3.04) |
para o caso em que N
mathend000# é finito. Quando N
mathend000# é infinito e quando o somatório se transforma em integral temos que
L[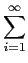 aixi(t)] aixi(t)] |
= |
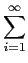 aiL[xi(t)] aiL[xi(t)] |
|
| |
= |
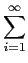 aiyi(t), aiyi(t), |
(2-3.05) |
e ainda que
L[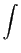 a(u)x(t, u)du] = a(u)x(t, u)du] = 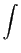 a(u)L[x(t, u)]du. a(u)L[x(t, u)]du.
|
(2-3.06) |
mathend000#
Neste caso dizemos que L é um operador linear e invariante no tempo. Por extensão, um sistema que implemente o operador L é chamado um Sistema Linear e Invariante no Tempo (SLIT).
No caso discreto temos, de forma idêntica a (2-3.4), que o operador L
mathend000# é linear se e só se
L[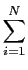 aixi[k]] aixi[k]] |
= |
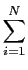 aiL[xi[k]] aiL[xi[k]] |
|
| |
= |
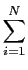 aiyi[k], aiyi[k], |
(2-3.07) |
e invariante no tempo se
L[x[k - k0]] = y[k - k0], 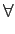 k0 k0 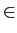 Z. Z.
|
(2-3.08) |
mathend000#
Convém agora definir conjuntos de sinais de excitação ``convenientes''.
O impulso de Dirac - definição
No sentido estritamente matemático o impulso de Dirac não é uma função mas sim uma entidade matemática que toma o nome de função generalizada ou distribuição. Para mais detalhes ver, por exemplo, Guelfand e Chilov [2]. A nossa aproximação será mais intuitiva do que matematicamente exacta, o que é largamente suficiente para as necessidades em teoria do sinal e outras aplicações em electrónica e comunicações. Podemos definir o impulso de Dirac como o limite da sequência de funções pares pn(x)
mathend000# tal que
e que
  (x)dx = (x)dx =  pn(x)dx = 1, pn(x)dx = 1, 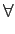 n n
|
(2-3.10) |
mathend000#
Uma sequência de funções que tem as propriedades desejadas é a definida por
pn(x) = ![$\displaystyle \left\{\vphantom{
\begin{array}{ll}
\displaystyle{1/n,} & x \in [-n/2,n/2]\\
0, & {\rm outro}~x.
\end{array} }\right.$](img48.png) ![$\displaystyle \begin{array}{ll}
\displaystyle{1/n,} & x \in [-n/2,n/2]\\
0, & {\rm outro}~x.
\end{array}$](img49.png)
|
(2-3.11) |
mathend000#
e que de alguma forma é aparentada à função porta usualmente utilizada em teoria do sinal.
No caso do Dirac discreto temos a seguinte definição
d[k] = 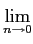 pn[k] = pn[k] = 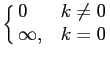 . .
|
(2-3.12) |
mathend000#
Propriedades:
1) a primeira e principal propriedade do impulso de Dirac é denominada sifting property e define-se por
  (x - a)g(x)dx = g(a), (x - a)g(x)dx = g(a),
|
(2-3.13) |
mathend000#
quando a função g(x)
mathend000# é contínua no ponto a
mathend000#. Quando g(x)
mathend000# tem uma discontinuidade em a
mathend000# então a sifting property resulta em
  (x - a)g(x)dx = (x - a)g(x)dx = 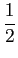 [g(a-) + g(a+)]. [g(a-) + g(a+)].
|
(2-3.14) |
mathend000#
Podemos facilmente demonstrar (2-3.13) utilizando (2-3.11) e fazendo tender n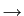 0
mathend000#. Assim (2-3.13) escreve-se
0
mathend000#. Assim (2-3.13) escreve-se
 pn(x - a)g(x)dx = pn(x - a)g(x)dx = 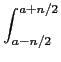 pn(x - a)g(x)dx, pn(x - a)g(x)dx,
|
(2-3.15) |
mathend000#
dado que
pn(x)g(x)
mathend000# é zero fora do intervalo considerado. Tomando o limite de (2-3.15) temos
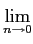 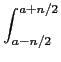 pn(x - a)g(x)dx pn(x - a)g(x)dx |
= |
g(a)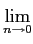 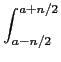 pn(x - a)dx pn(x - a)dx |
|
| |
= |
g(a), |
(2-3.16) |
visto que quando n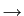 0
mathend000# g(x) será aproximadamente constante e igual a g(a)
mathend000# este pode sair do integral que por si só representa a superfície da função pn(x)
mathend000# que devido a (2-3.10) é igual a 1.
0
mathend000# g(x) será aproximadamente constante e igual a g(a)
mathend000# este pode sair do integral que por si só representa a superfície da função pn(x)
mathend000# que devido a (2-3.10) é igual a 1.
2) as derivadas sucessivas do impulso de Dirac encontram-se ligadas pela relação
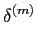 (t) = (- 1)mm! (t) = (- 1)mm!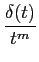 . .
|
(2-3.17) |
mathend000#
Esta relação demonstra-se começando por notar que devido a (2-3.9)
x (x) = 0, (x) = 0,
|
(2-3.18) |
mathend000#
cuja derivada se escreve
x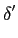 (x) + (x) +  (x) = 0, (x) = 0,
|
(2-3.19) |
mathend000#
e que nos permite escrever
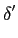 (x) = - (x) = - 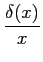 , ,
|
(2-3.20) |
mathend000#
o que nos dá (2-3.17) por derivação sucessiva.
3) outra propriedade útil do Dirac é
 g(t) g(t)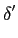 (t - a)dt = g'(a). (t - a)dt = g'(a).
|
(2-3.21) |
mathend000#
4) e ainda outras propriedades
 g(t) g(t)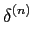 (t - a)dt (t - a)dt |
= |
(- 1)ng(n)(a), |
(2-3.22) |
 (- t) (- t) |
= |
 (t), (t), |
(2-3.23) |
 (at) (at) |
= |
 (t)/|a|, (t)/|a|, |
(2-3.24) |
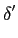 (- t) (- t) |
= |
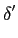 (t), (t), |
(2-3.25) |
  (a - t) (a - t) (t - b)dt (t - b)dt |
= |
 (a - b), (a - b), |
(2-3.26) |
g(t)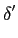 (t) (t) |
= |
g'(0) (t) + g(0) (t) + g(0)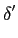 (t). (t). |
(2-3.27) |
truemm
Figura 2.1:
aproximação da função degrau unidade.
|
![\includegraphics[height=40mm,width=90mm]{figs/step-function.eps}](img59.png) |
Fazendo o integral de (2-3.11) (figura 2.1) obtemos para n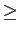 0
mathend000#,
0
mathend000#,
 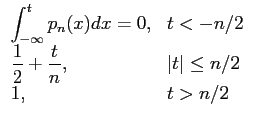
|
(2-3.28) |
mathend000#
que, quando n 0
mathend000#, tende para a função degrau unidade u(t)
mathend000# definida por
0
mathend000#, tende para a função degrau unidade u(t)
mathend000# definida por
u(t) = 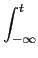  (x)dx (x)dx |
= |
0, t < 0 |
|
| |
= |
1, t > 0 |
(2-3.29) |
temos então que
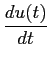 = u'(t) = = u'(t) =  (t). (t).
|
(2-3.30) |
mathend000#
Sinais de entrada: respostas indicial e impulsiva
A utilidade das propriedades dos sistemas lineares é amplamente justificada pelo facto de que se um determinado sinal puder ser decomposto numa soma de funções de base então podemos calcular a resposta de um sistema linear conhecendo apenas a resposta do sistema às funções de base. Para concretizar este aspecto será necessário rever as noções de resposta indicial e resposta impulsiva.
a resposta de um sistema (inicialmente em repouso) a um degrau unidade é por definição a resposta indicial, a(t)
mathend000#. Esta resposta, que representa o sistema no domínio do tempo, permite determinar o sinal de saída de um sistema quando o sinal de entrada é decomponível numa soma de funções degrau unidade ponderadas em amplitude e atrasadas umas em relação às outras. Pode-se além disso demonstrar que qualquer função em geral se pode decompor numa soma infinita de degraus ponderados e atrasados - este facto leva directamente à noção de integral de convolução.
Exemplo: tomemos como exemplo o caso do circuito CR da figura 2.2(a). Pretende-se, num primeiro tempo, calcular a resposta indicial a(t)
mathend000# do circuito e num segundo tempo a resposta ao sinal de entrada e1(t)
mathend000# representado na figura 2.2(b).
Figura 2.2:
circuito CR (a) e função em escada (b).
|
![\includegraphics[height=40mm,width=90mm]{figs/circuito-CR.eps}](img65.png) |
Solução: a lei da malhas aplicada na malha única da figura 2.2(a)permite-nos escrever as seguintes equações:
mathend000#
onde vc(t)
mathend000# é a tensão aos terminais do condensador C
mathend000#. Substituindo para i(t)
mathend000# da (3) na (2) temos que
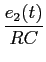 = = 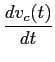 . .
|
(2-3.31) |
mathend000#
Derivando (1) em relação a t
mathend000# obtemos
e substituindo finalmente (2-3.31) nesta última equação permite escrever a equação que rege este circuito como
onde  = RC
mathend000# é a constante de tempo do circuito. A solução desta equação obtem-se de forma clássica como a soma da solução geral da equação sem segundo membro (equação homogénea) com uma solução particular da equação com segundo membro (ver disciplinas de Análise Matemática). Assim a solução geral da equação homogénea escreve-se
= RC
mathend000# é a constante de tempo do circuito. A solução desta equação obtem-se de forma clássica como a soma da solução geral da equação sem segundo membro (equação homogénea) com uma solução particular da equação com segundo membro (ver disciplinas de Análise Matemática). Assim a solução geral da equação homogénea escreve-se
e2'(
t) =
Ae-t/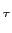 u
u(
t),
mathend000#
onde u(t)
mathend000# é a função degrau unidade e A
mathend000# é uma constante a determinar.A solução particular da equação com segundo membro se obtem para t > 0
mathend000# e quando
e1(t) = u(t)
mathend000#, degrau unidade, como
e2''(
t) =
Be-t/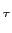 u
u(
t),
mathend000#
e por isso a solução geral é da forma
e2(
t) =
Ke-t/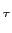 u
u(
t),
mathend000#
onde K
mathend000# é uma constante que depende dos valores iniciais da tensão aplicada, que no caso do degrau unidade, permite dizer que K = 1
mathend000# e assim a resposta indicial deste sistema é
a(
t) =
e-t/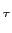 u
u(
t)
mathend000#
A resposta e2(t)
mathend000# quando e1(t)
mathend000# é o sinal da figura 2.2(b) obtem-se a partir da resposta indicial a(t)
mathend000# notando que e1(t)
mathend000# se pode escrever como uma série de funções degrau unidade
e1(t) = 2u(t) + 4u(t - 1) - 6u(t - 2)
mathend000#
e neste caso, visto que se trata de um SLIT - sistema linear e invariante no tempo, a resposta é simplesmente
| e2(t) |
= |
2a(t) + 4a(t - 1) - 6a(t - 2) |
|
| |
= |
2e-t/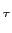 u(t) + 4e-(t-1)/ u(t) + 4e-(t-1)/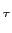 u(t - 1) + 6e-(t-2)/ u(t - 1) + 6e-(t-2)/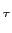 u(t - 2). u(t - 2). |
|
a resposta de um sistema (inicialmente em repouso) a um impulso de Dirac unitário é por definição a resposta impulsiva, h(t)
mathend000#. Visto que o impulso de Dirac é a derivada (no sentido lato) do degrau unidade, podemos dizer que a resposta impulsiva é a derivada da resposta indicial. Como no caso da resposta indicial, conhecendo a resposta impulsiva de um sistema linear podemos determinar a resposta a qualquer sinal representado por uma série infinita de impulsos de Dirac ponderados e atrasados uns em relação aos outros.
Exemplo: a resposta impulsiva de um dado sistema linear é h(t)
mathend000#. Determine a resposta do sistema a uma excitação
x(
t) = 2

(
t) + 4

(
t - 1) - 6

(
t - 2)
mathend000#
Solução: por superposição podemos dizer que a resposta y(t)
mathend000# se escreve
y(t) = 2h(t) + 4h(t - 1) - 6h(t - 2)
mathend000#
Existem várias formas de introduzir a noção de resposta impulsiva. Adoptaremos uma forma intuitiva começando pela noção de impulsão breve e impulsão de Dirac. Como é evidente, impulsos de Dirac não existem no mundo real. Porém impulsos ''breves'' são perfeitamente realizáveis, o que passa pela definição do que se entende por ''breve''. ''Breve'' em relação a quê ? Vamos, por exemplo, considerar o caso de um impulso - por enquanto de forma temporal indeterminada - e de duração 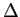 mathend000#. Este impulso é aplicado à entrada de um sistema linear de resposta impulsiva h(t)
mathend000# cujo ''tempo de resposta'' é definido seja pelo seu período (no caso de um sistema oscilante) seja pela sua constante de tempo (no caso de um sistema amortecido).
mathend000#. Este impulso é aplicado à entrada de um sistema linear de resposta impulsiva h(t)
mathend000# cujo ''tempo de resposta'' é definido seja pelo seu período (no caso de um sistema oscilante) seja pela sua constante de tempo (no caso de um sistema amortecido).
Vamos supôr arbitrariamente que o tempo de resposta no nosso caso é 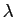 mathend000#. Neste caso podemos aceitar com alguma facilidade que o impulso seja breve em relação a h(t)
mathend000# se
mathend000#. Neste caso podemos aceitar com alguma facilidade que o impulso seja breve em relação a h(t)
mathend000# se
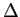 < <
< < 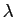 mathend000#. A vantagem é que neste caso a resposta do sistema ao impulso ''breve'' se encontra facilmente e é dada por
onde A
mathend000# é a área contida sob o impulso e tem a ver com o facto que se a resposta impulsiva h(t)
mathend000# é a resposta do sistema a um impulso de Dirac de área unitária (ver integral (2-3.10)) então se o impulso tiver área A
mathend000# então a resposta será simplesmente Ah(t)
mathend000#. Justificaremos mais adiante o facto de que esta resposta só é válida para
t >
mathend000#. A vantagem é que neste caso a resposta do sistema ao impulso ''breve'' se encontra facilmente e é dada por
onde A
mathend000# é a área contida sob o impulso e tem a ver com o facto que se a resposta impulsiva h(t)
mathend000# é a resposta do sistema a um impulso de Dirac de área unitária (ver integral (2-3.10)) então se o impulso tiver área A
mathend000# então a resposta será simplesmente Ah(t)
mathend000#. Justificaremos mais adiante o facto de que esta resposta só é válida para
t > 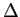 mathend000#.
mathend000#.
Exemplo: mais uma vez fazemos apelo a um circuito eléctrico, como aquele representado na figura 2.3. Determinar a resposta e2(t)
mathend000# do circuito da figura 2.3(a), ao impulso triangular representado na figura 2.3(b).
truemm
Figura 2.3:
circuito RL (a) e função triangular de duração 0.2 segundos (b).
|
![\includegraphics[height=50mm,width=100mm]{figs/circuito-RL.eps}](img75.png) |
Solução: demonstra-se que este circuito simples composto por uma bobine e uma resistência é regido pela equação diferencial de primeira ordem e coeficientes constantes com segundo membro do tipo
e1(
t) = 2
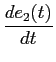
+
e2(
t)
mathend000#
a partir da qual utilizando exactamente o mesmo raciocínio que no exemplo anterior mas neste caso para um sinal de entrada do tipo impulso de Dirac obtemos
e2'(t) = Ae-t/2u(t),
mathend000#
para a solução geral da equação sem segundo membro,
e2''(t) = Be-t/2u(t),
mathend000#
para a solução forçada da equação com segundo membro e onde se obtém a solução geral sob a forma
e2(
t) =
h(
t) =
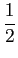 e-t/2u
e-t/2u(
t),
mathend000#
onde o coeficiente 1/2
mathend000# vem do facto das condições iniciais para t = 0
mathend000# onde a tensão
e2(0) = 1/2
mathend000#. Pode-se assim ver que o tempo de resposta do sistema ou constante de tempo é 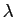 = 2
mathend000# s. Visto que a duração do impulso é de 0.2 s, verifica-se bem que a constante de tempo
= 2
mathend000# s. Visto que a duração do impulso é de 0.2 s, verifica-se bem que a constante de tempo
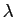 > > 0.2
mathend000# o que faz com que possamos considerar o impulso como ''breve''.
> > 0.2
mathend000# o que faz com que possamos considerar o impulso como ''breve''.
Figura 2.4:
resposta de um circuito RL a um função triangular.
|
![\includegraphics[height=60mm,width=120mm]{figs/resp-circuito-RL.eps}](img76.png) |
A superfície do impulso triangular é dada por
A = 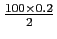 = 10
mathend000#, por isso podemos aproximar
= 10
mathend000#, por isso podemos aproximar
e1(
t)
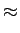
10

(
t)
mathend000#
e nesse caso a resposta escreve-se
e2(t) = h(t) * e1(t)
mathend000# ou seja
e2(
t)
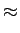
5
e-t/2u(
t)
mathend000#
A figura 2.4 mostra, num mesmo sistema de eixos, o sinal de entrada e1(t)
mathend000#, a resposta exacta e a resposta aproximada e2(t)
mathend000#. Podemos facilmente notar que a diferença entre as respostas exacta e aproximada é significativo apenas durante a duração - breve - do sinal de entrada, i.e., aproximadamente 0.2 segundos. A partir desse ponto a solução aproximada e a solução exacta são muito semelhantes e poderemos então dizer que a aproximação é muito boa para t > 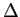 mathend000#.
mathend000#.
O produto de convolução é o resultado da generalização da resposta de um sistema linear invariante a uma função arbitrária. A função arbitrária poderá ser representada seja por uma soma de impulsos de Dirac seja por uma soma de degraus unidade.
truemm
Figura 2.5:
aproximação por uma série de rectângulos.
![\includegraphics[height=60mm]{figs/aprox-Dirac.eps}](img79.png) |
Consideremos a figura 2.5 onde o sinal de entrada x(t)
mathend000# se encontra aproximado graficamente por uma série de rectângulos de duração
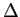
 mathend000# e de amplitude
x(
mathend000# e de amplitude
x(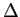
 )
mathend000#. Devemos considerar que as funções rectangulares são ''breves'' em relação a x(t)
mathend000# o que é equivalente a considerar que o sinal x(t)
mathend000# varia pouco durante a duração de cada impulso rectangular. Consideremos agora o impulso de ordem n
mathend000#: a sua área An
mathend000# é igual a
An = x(n
)
mathend000#. Devemos considerar que as funções rectangulares são ''breves'' em relação a x(t)
mathend000# o que é equivalente a considerar que o sinal x(t)
mathend000# varia pouco durante a duração de cada impulso rectangular. Consideremos agora o impulso de ordem n
mathend000#: a sua área An
mathend000# é igual a
An = x(n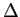
 )
)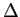
 mathend000#, se considerarmos que a sua largura
mathend000#, se considerarmos que a sua largura
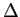
 < <
< < 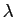 mathend000#, onde
mathend000#, onde 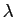 mathend000# é a constante de tempo do sistema podemos aproximar cada rectângulo por um impulso de Dirac de forma
An
mathend000# é a constante de tempo do sistema podemos aproximar cada rectângulo por um impulso de Dirac de forma
An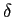 (t - n
(t - n )
mathend000#. Este impulso provoca no sistema uma resposta
Anh(t - n
)
mathend000#. Este impulso provoca no sistema uma resposta
Anh(t - n )
mathend000#. Para obter a resposta global ao sinal x(t)
mathend000# temos que fazer o somatório discreto de um número infinito de impulsos rectangulares, ou Diracs se fizermos a aproximação
)
mathend000#. Para obter a resposta global ao sinal x(t)
mathend000# temos que fazer o somatório discreto de um número infinito de impulsos rectangulares, ou Diracs se fizermos a aproximação
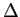
 < <
< < 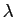 mathend000#, tal que
mathend000#, tal que
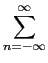 [x(n [x(n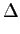  ) )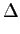  ] ] (t - n (t - n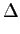  ) ) 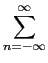 [x(n [x(n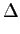  ) )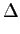  ]h(t - n ]h(t - n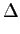  ), ),
|
(2-3.35) |
mathend000#
quanto mais
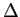

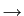 0
mathend000# melhor será a aproximação de x(t)
mathend000# pela série de rectângulos. No limite, teremos que
0
mathend000# melhor será a aproximação de x(t)
mathend000# pela série de rectângulos. No limite, teremos que
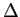

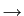 d
d mathend000# e assim
mathend000# e assim
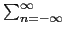
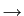
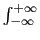 mathend000# e
n
mathend000# e
n

 nd
nd =
=  mathend000#. Assim, passando ao limite, a equação anterior escreve-se
mathend000#. Assim, passando ao limite, a equação anterior escreve-se
 x( x( ) ) (t - (t -  )d )d 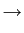  x( x( )h(t - )h(t -  )d )d , ,
|
(2-3.36) |
mathend000#
em poucas palavras podemos dizer que a expressão à esquerda é o sinal x(t)
mathend000# de excitação do sistema e a expressão do lado direito é a resposta y(t)
mathend000# do sistema a essa mesma excitação, assim, sob forma de equação podemos escrever,
y(t) =  x( x( )h(t - )h(t -  )d )d . .
|
(2-3.37) |
mathend000#
Esta última expressão é a relação procurada e chama-se integral de convolução. De uma forma abreviada, podemos notar (2-3.37) como
|
y(t) = x(t) * h(t).
|
(2-3.38) |
mathend000#
No exemplo anterior, se o sinal x(t)
mathend000# fosse considerado como sendo igual a zero para t < 0
mathend000# (dir-se-ia que x(t)
mathend000# seria um sinal causal) e a equação de convolução (2-3.37) seria dada por
y(t) = 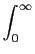 x( x( )h(t - )h(t -  )d )d , ,
|
(2-3.39) |
mathend000#
onde o limite inferior do integral passou a ser 0. Ainda se ambos os sinais, x(t)
mathend000# e a resposta impulsiva h(t)
mathend000#, forem causais teríamos que
h(t -  )
) 0
mathend000# para
t -
0
mathend000# para
t - 
 0
mathend000# ou seja para
0
mathend000# ou seja para

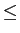 t
mathend000# e nesse caso o integral de convolução toma a forma
t
mathend000# e nesse caso o integral de convolução toma a forma
y(t) = 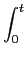 x( x( )h(t - )h(t -  )d )d . .
|
(2-3.40) |
mathend000#
Antes de passarmos aos exemplos devemos referir a equação de convolução para o caso de sinais e sistemas discretos. Utilizando (2-3.37) podemos escrever
y[k] = 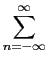 x[n]h[k - n], x[n]h[k - n],
|
(2-3.41) |
mathend000#
que para o caso em que tanto o sistema como o sinal de entrada são causais, se reduz a
y[k] = 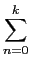 x[n]h[k - n], x[n]h[k - n],
|
(2-3.42) |
mathend000#
em pleno acordo com (2-3.40).
Exemplo: a título de exemplo podemos mencionar o sistema dado pela equação entrada-saída
|
y(t) = x(t - t0),
|
(2-3.43) |
mathend000#
onde se pretende determinar a resposta impulsiva do sistema h(t)
mathend000#. Utilizando a propriedade de sifting (2-3.13) notamos que esta nos permite escrever o sinal x(t - t0)
mathend000# como
x(t - t0) =   (t - t0 - (t - t0 -  )x( )x( )d )d , ,
|
(2-3.44) |
mathend000#
de onde por identificação
h(t) =  (t - t0), (t - t0),
|
(2-3.45) |
mathend000#
é a resposta impulsiva do sistema procurado.
sem prejuízo do resultado, e para simplificar, vamos considerar que ambos os sinais a convoluir são causais, assim o integral de convolução escreve-se
y(t) = 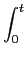 x( x( )h(t - )h(t -  )d )d
|
(2-3.46) |
mathend000#
o que implica uma sucessão de cinco operações:
- mudança de variável
- dobragem de uma função (rotação)
- atraso de t
mathend000# em relação a
 mathend000#
mathend000#
- produto entre as funções
- integração
Figura 2.6:
convolução gráfica.
![\includegraphics[height=200mm]{figs/convol-grafica.eps}](img92.png) |
Consideremos a figura 2.6 através da qual podemos seguir as operações da convolução passo a passo. A primeira operação muda apenas as variáveis de t
mathend000# em  mathend000#, variável de integração. A segunda operação executa uma rotação de 180 graus em torno do eixo das ordenadas para a função h(
mathend000#, variável de integração. A segunda operação executa uma rotação de 180 graus em torno do eixo das ordenadas para a função h( )
mathend000# de forma a obter h(-
)
mathend000# de forma a obter h(-  )
mathend000#: a esta operação chamamos dobragem ou rotação de 180 graus. A terceira operação consiste no atraso de t
mathend000# de uma função já dobrada para de h(-
)
mathend000#: a esta operação chamamos dobragem ou rotação de 180 graus. A terceira operação consiste no atraso de t
mathend000# de uma função já dobrada para de h(-  )
mathend000# obter h(t -
)
mathend000# obter h(t -  )
mathend000#. Estas duas últimas operações de dobragem e atraso são obviamente permutáveis sendo possível fazer primeiro o atraso e só depois a dobragem. O produto das duas funções permite obter a função f (t,
)
mathend000#. Estas duas últimas operações de dobragem e atraso são obviamente permutáveis sendo possível fazer primeiro o atraso e só depois a dobragem. O produto das duas funções permite obter a função f (t, )
mathend000# da figura 2.6. o resultado do integral é a superfície sob esta função, dando o valor do resultado y(t)
mathend000#. Fazendo variar o valor de t
mathend000#, i.e., deslocado de novo h(t -
)
mathend000# da figura 2.6. o resultado do integral é a superfície sob esta função, dando o valor do resultado y(t)
mathend000#. Fazendo variar o valor de t
mathend000#, i.e., deslocado de novo h(t -  )
mathend000# em relação a x(
)
mathend000# em relação a x( )
mathend000# permite-nos obter finalmente a função resultante y(t)
mathend000# para qualquer t
mathend000#.
)
mathend000# permite-nos obter finalmente a função resultante y(t)
mathend000# para qualquer t
mathend000#.
Exemplo: um sistema é representado pela sua resposta impulsiva h(t)
mathend000#, tal que h(t) = 0
mathend000#, para t < 0
mathend000#. Determinar por convolução, a resposta y(t)
mathend000# à excitação x(t)
mathend000# definida por
x(
t) =
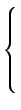
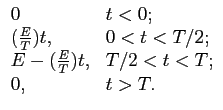
mathend000#
Solução: encontra-se facilmente usando x( )
mathend000# por substituição de t
mathend000# por
)
mathend000# por substituição de t
mathend000# por  mathend000# na função acima e fazendo a convolução com h(t -
mathend000# na função acima e fazendo a convolução com h(t -  )
mathend000#,
)
mathend000#,
| t < 0 |
y(t) = 0, |
| 0 < t < T/2, |
y(t) = 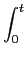 ( (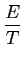 ) ) h(t - h(t -  )d )d , , |
| T/2 < t < T, |
y(t) = 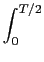 ( (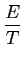 ) ) h(t - h(t -  )d )d + + 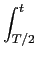 E(1 - E(1 - 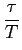 )h(t - )h(t -  )d )d , , |
| T < t, |
y(t) = 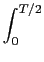 ( (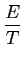 ) ) h(t - h(t -  )d )d + + 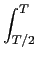 E(1 - E(1 - 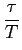 )h(t - )h(t -  )d )d . . |
mathend000#
os argumentos t -  mathend000# e
mathend000# e  mathend000# no integral de convolução podem ser permutados, o que se obtem a partir da definição
mathend000# no integral de convolução podem ser permutados, o que se obtem a partir da definição
| y(t) |
= |
x(t) * h(t) |
|
| |
= |
 x(t - x(t -  )h( )h( )d )d |
(2-3.47) |
fazendo a mudança de variável
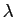 = t -
= t -  mathend000#, obtendo-se
mathend000#, obtendo-se
| y(t) |
= |
-  x( x(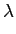 )h(t - )h(t - 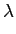 )d )d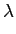 |
|
| |
= |
 x( x(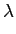 )h(t - )h(t - 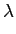 )d )d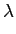 |
|
| |
= |
h(t) * x(t), |
(2-3.48) |
o que é equivalente a demonstrar que
|
x(t) * h(t) = h(t) * x(t),
|
(2-3.49) |
mathend000#
e portanto o produto de convolução é comutativo.
vamos supôr que
y(t) =  x( x( )h(t - )h(t -  )d )d , ,
|
(2-3.50) |
mathend000#
derivando em relação a t
mathend000# temos
y(1)(t) = 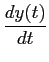 = =  x( x( ) )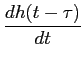 d d + +  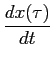 h(t - h(t -  )d )d , ,
|
(2-3.51) |
mathend000#
expressão na qual o segundo termo é nulo visto que x( )
mathend000# não depende de t
mathend000#. Assim podemos escrever que
)
mathend000# não depende de t
mathend000#. Assim podemos escrever que
y(1)(t) =  x( x( )h(1)(t - )h(1)(t -  )d )d = =  x(1)(t - x(1)(t -  )h( )h( )d )d , ,
|
(2-3.52) |
mathend000#
utilizando facto da comutatividade do produto de convolução. De uma forma geral temos que
|
y(n)(t) = x(n)(t) * h(t) = x(t) * h(n)(t),
|
(2-3.53) |
mathend000#
se a função de excitação é um Dirac a resposta do sistema é simplesmente
| y(t) |
= |
 h( h( ) ) (t - (t -  )d )d |
|
| |
= |
  ( ( )h(t - )h(t -  )d )d |
|
| |
= |
h(t), |
(2-3.54) |
devido à propriedade (2-3.13). Assim, como aliás o seu nome indica, a resposta de um sistema a um impulso é a resposta impulsiva.
A equação (2-3.54) permite-nos escrever uma relação simples mas suficientemente importante que é
h(t) =  h( h( ) ) (t - (t -  )d )d , ,
|
(2-3.55) |
mathend000#
ou seja, por palavras: qualquer função x(t)
mathend000# pode ser representada por uma soma contínua de impulsos de Dirac ponderados.
a resposta de um sistema linear a um degrau unidade u(t)
mathend000# é chamada a resposta indicial e é representada por a(t)
mathend000#,
| a(t) |
= |
h(t) * u(t) |
|
| |
= |
 h( h( )u(t - )u(t -  )d )d |
|
| |
= |
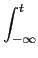 h( h( )d )d . . |
(2-3.56) |
Devido à relação (2-3.53) podemos escrever a derivada da resposta indicial a(t)
mathend000# como
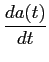 = h(t) * = h(t) * 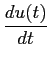 = h(t) * = h(t) *  (t) = h(t), (t) = h(t),
|
(2-3.57) |
mathend000#
o que define a derivada da resposta indicial como sendo igual à resposta impulsiva.
Exemplo: considere um sistema cuja resposta impulsiva é
h(t) = u(t) - u(t - t0)
mathend000#, com t0 > 0
mathend000#.
- qual a resposta do sistema a um sinal de entrada
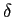 (t)
mathend000# ? E a
(t)
mathend000# ? E a
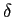 (t - t0)
mathend000# ?
(t - t0)
mathend000# ?
- calcule e presente a resposta indicial a(t)
mathend000# do sistema ?
- calcule e represente a resposta do sistema a um sinal de entrada
x(t) = u(t) - u(t - t0)
mathend000#.
Sistemas estáveis
Por definição um sistema linear é dito estável se, qualquer sinal de entrada limitado produz um sinal de saída também limitado. Podemos igualmente deduzir a condição necessária para a resposta impulsiva do sistema. Partindo do integral de convolução
y(t) =  h( h( )x(t - )x(t -  )d )d , ,
|
(2-4.01) |
mathend000#
e tomando o valor absoluto em ambos os lados
| |y(t)| |
= |
| h( h( )x(t - )x(t -  )d )d | | |
|
| |
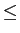 |
 |h( |h( )||x(t - )||x(t -  )|d )|d , , |
(2-4.02) |
se o sinal de entrada x(t)
mathend000# é limitado, quer dizer que existe pelo menos um valor M
mathend000# tal que
e portanto (2-4.2) pode-se escrever
|y(t)|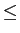 M M |h( |h( )|d )|d , , 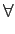 t t
|
(2-4.04) |
mathend000#
que será finito se e só se
de onde podemos deduzir a condição de estabilidade para um sistema que é que a sua resposta impulsiva deverá ser absolutamente integrável - equação (2-4.5).
Sistemas causais
Como já tivemos a ocasião de referir anteriormente um sistema é causal se a sua resposta impulsiva h(t) = 0
mathend000# para t < 0
mathend000#. A consequência directa é de que a resposta se escreverá então
y(t) = 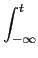 x( x( )h(t - )h(t -  )d )d , ,
|
(2-5.01) |
mathend000#
se o sinal de entrada x(t)
mathend000# for aplicado no instante t0
mathend000# e for zero antes desse instante então temos que
y(t) = 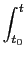 x( x( )h(t - )h(t -  )d )d , ,
|
(2-5.02) |
mathend000#
por outras palavras a resposta do sistema será igual a zero para t < t0
mathend000#, i.e., antes de ser aplicado sinal de entrada, ou ainda que a resposta não pode preceder a excitação. Para além da causalidade e estabilidade existe ainda a noção de realizabilidade. De uma forma genérica diz-se que um sistema é realizável se ele é simultaneamente causal e estável.
Alguns exemplos de sistemas lineares podem ser, por exemplo, o sistema cuja saída se escreve
y(t) = x (t) = (t) = 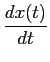 , ,
|
(2-6.01) |
mathend000#
comparação com a propriedade (2-3.53) leva-nos a escrever que neste caso
h(t) = 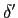 (t)
mathend000# e portanto,
(t)
mathend000# e portanto,
x'(t) = x(t) * 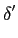 (t), (t),
|
(2-6.02) |
mathend000#
o que é mesmo assim um resultado notável.
Outro exemplo é o caso do integral num intervalo T
mathend000# limitado
y(t) = 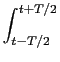 x(u)du, x(u)du,
|
(2-6.03) |
mathend000#
trata-se portanto de um sistema apenas 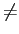 0
mathend000# no intervalo
[- T/2, T/2]
mathend000#, e a sua resposta impulsiva escreve-se
0
mathend000# no intervalo
[- T/2, T/2]
mathend000#, e a sua resposta impulsiva escreve-se
onde rect é a função porta, neste caso de duração T
mathend000#.
Consideremos de novo o exemplo do circuito da figura 2.2, no qual o sinal de entrada e de saída se encontram ligados pela equação diferencial (2-3.33). Esta é uma forma alternativa de representar sistemas lineares invariantes no tempo (ver p.ex. sebenta de Análise de Circuitos [3]), cuja forma geral se pode escrever
onde x(t)
mathend000# e y(t)
mathend000# são respectivamente a entrada e a saída do sistema e
d0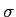 (t)/dt0 =
(t)/dt0 = 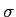 (t)
mathend000#. Esta representação só é válida para os sistemas inertes, ou seja, os sistemas que estão no seu estado de repouso quando a excitação é aplicada. De algum modo o sistema linear é caracterizado pelos coeficientes
ai
(t)
mathend000#. Esta representação só é válida para os sistemas inertes, ou seja, os sistemas que estão no seu estado de repouso quando a excitação é aplicada. De algum modo o sistema linear é caracterizado pelos coeficientes
ai mathend000# e
bi
mathend000# e
bi mathend000# e sobretudo pelas ordens N
mathend000# e M
mathend000# da equação diferencial. No caso do exemplo temos simplesmente que N = M = 1
mathend000# com a0 = 1
mathend000#, a1 = RC
mathend000#, b0 = 0
mathend000# e b1 = RC
mathend000#. A discretização desta equação pode ser feita sabendo que a derivada de ordem um é dada por
que pode ser aproximada por
mathend000# e sobretudo pelas ordens N
mathend000# e M
mathend000# da equação diferencial. No caso do exemplo temos simplesmente que N = M = 1
mathend000# com a0 = 1
mathend000#, a1 = RC
mathend000#, b0 = 0
mathend000# e b1 = RC
mathend000#. A discretização desta equação pode ser feita sabendo que a derivada de ordem um é dada por
que pode ser aproximada por
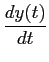 = = ![$\displaystyle {{y[nT+T] - y[nT]}\over T}$](img124.png) , ,
|
(2-7.03) |
mathend000#
para T
mathend000# suficientemente pequeno (condição de amostragem ideal). Sem prejuízo do resultado podemos considerar T = 1
mathend000#, o que simplifica a demonstração para derivadas de ordem superior, e escrever (2-7.1) como
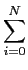 aiy[n - i] = aiy[n - i] = 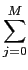 bjx[n - j], bjx[n - j],
|
(2-7.04) |
mathend000#
onde os ai
mathend000# e bj
mathend000# são calculados a partir dos
ai mathend000# e
bj
mathend000# e
bj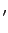 mathend000# e com aN
mathend000# e com aN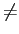 0
mathend000#. Esta é chamada a equação de diferenças com coeficientes constantes e permite determinar o sinal de saída do sistema y[n]
mathend000# a partir das amostras do sinal de entrada e dos seus valores a instantes anteriores, o que torna esta equação de tipo recursivo. Para melhor notar este facto podemos escrever a equação (2-7.4) sob a forma
0
mathend000#. Esta é chamada a equação de diferenças com coeficientes constantes e permite determinar o sinal de saída do sistema y[n]
mathend000# a partir das amostras do sinal de entrada e dos seus valores a instantes anteriores, o que torna esta equação de tipo recursivo. Para melhor notar este facto podemos escrever a equação (2-7.4) sob a forma
y[n] = - 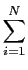 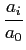 y[n - i] + y[n - i] + 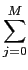 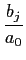 x[n - j], x[n - j],
|
(2-7.05) |
mathend000#
onde se assumiu que a0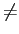 0
mathend000#. Podemos então notar que a saída a um dado instante é a soma de dois termos: um que é obtido quando x[n] = 0
mathend000#, i.e., quando não é aplicado nenhum sinal à entrada e só depende do próprio sinal de saída e do estado inicial do sistema (solução homógenea) e outro que depende da entrada x[n]
mathend000# e é normalmente chamada solução forçada. Veremos mais à frente que a resposta impulsiva h[n]
mathend000# do sistema pode ser expressa através dos coeficientes ai
mathend000# e bj
mathend000# da equação de diferenças.
0
mathend000#. Podemos então notar que a saída a um dado instante é a soma de dois termos: um que é obtido quando x[n] = 0
mathend000#, i.e., quando não é aplicado nenhum sinal à entrada e só depende do próprio sinal de saída e do estado inicial do sistema (solução homógenea) e outro que depende da entrada x[n]
mathend000# e é normalmente chamada solução forçada. Veremos mais à frente que a resposta impulsiva h[n]
mathend000# do sistema pode ser expressa através dos coeficientes ai
mathend000# e bj
mathend000# da equação de diferenças.
Podemos facilmente generalizar o conceito de sistema e resposta impulsiva, ao caso de múltiplas entradas e múltiplas saídas. O número de entradas J
mathend000# não necessita de ser igual ao número de saídas I
mathend000#. Podemos facilmente escrever o sinal de saída como
yj(t) = 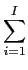 hij(t) * xi(t), j = 1,..., J, hij(t) * xi(t), j = 1,..., J,
|
(2-8.01) |
mathend000#
onde hij(t)
mathend000# represente a resposta impulsiva do sistema entre a entrada i
mathend000# e a saída j
mathend000#. Impõe-se aqui introduzir uma notação matricial
onde
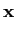 (t) = (t) =  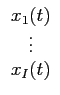 ![$\displaystyle \left.\vphantom{
\begin{array}{c}
x_1(t)\\
\vdots\\
x_I(t)
\end{array} }\right]$](img134.png) , ,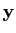 (t) = (t) = 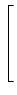 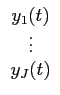 ![$\displaystyle \left.\vphantom{
\begin{array}{c}
y_1(t)\\
\vdots\\
y_J(t)
\end{array} }\right]$](img137.png) , ,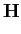 (t) = (t) = 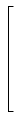 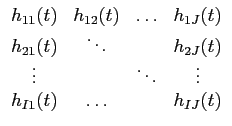 ![$\displaystyle \left.\vphantom{
\begin{array}{cccc}
h_{11}(t)& h_{12}(t)& \ld...
... & \ddots & \vdots \\
h_{I1}(t)& \ldots & &h_{IJ}(t)
\end{array}
}\right]$](img140.png) . .
|
(2-8.03) |
mathend000#
e 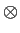 mathend000# é o operador convolução para o caso de matrizes. De notar no entanto que a equação de convolução matricial (2-8.2), contrariamente ao caso geral, não é comutativa, i.e., em geral
mathend000# é o operador convolução para o caso de matrizes. De notar no entanto que a equação de convolução matricial (2-8.2), contrariamente ao caso geral, não é comutativa, i.e., em geral
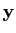 (t) = (t) = 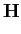 (t) (t) 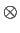 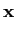 (t) (t)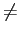 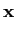 (t) (t)  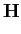 (t). (t).
|
(2-8.04) |
mathend000#
A passagem ao caso de sistemas complexos com entradas - e também saídas - complexas deduz-se do caso real a duas entradas e duas saídas, onde
| h(t) |
= |
hr(t) + jhi(t) |
(2-9.01) |
| x(t) |
= |
xr(t) + jxi(t) |
(2-9.02) |
| y(t) |
= |
yr(t) + jyi(t), |
(2-9.03) |
e daí
mathend000# podemos escrever
| y(t) |
= |
h(t) * x(t) |
|
| |
= |
[hr(t) + jhi(t)] * [xr(t) + jxi(t)] |
|
| |
= |
hr(t) * xr(t) - hi(t) * xi(t) + |
|
| |
|
+ j[hi(t) * xr(t) + hr(t) * xi(t)], |
(2-9.04) |
e agrupando partes reais e imaginárias
| yr(t) |
= |
hr(t) * xr(t) - hi(t) * xi(t) |
(2-9.05) |
| yi(t) |
= |
hi(t) * xr(t) + hr(t) * xi(t). |
(2-9.06) |
Fazendo uma analogia com o caso a 2 entradas - 2 saídas ((2-8.3) com I
mathend000#=2, e J
mathend000#=2) podemos fazer as seguintes equivalências
| hr(t) |
= |
h11(t) |
(2-9.07) |
| hi(t) |
= |
- h12(t) |
(2-9.08) |
| hr(t) |
= |
h22(t) |
(2-9.09) |
| hi(t) |
= |
h21(t), |
(2-9.10) |
e notar que a representação de um sistema complexo pode ser feita por um sistema real a 2 entradas - 2 saídas se e só se
| h11(t) |
= |
h22(t) |
(2-9.11) |
| h12(t) |
= |
- h21(t). |
(2-9.12) |
Sergio Jesus
2008-12-30
![]() t0.
t0.
![]() aixi(t)]
aixi(t)]![]() aiL[xi(t)]
aiL[xi(t)]![]() aiyi(t),
aiyi(t),![]() a(u)x(t, u)du] =
a(u)x(t, u)du] = ![]() a(u)L[x(t, u)]du.
a(u)L[x(t, u)]du.
![]() aixi[k]]
aixi[k]]![]() aiL[xi[k]]
aiL[xi[k]]![]() aiyi[k],
aiyi[k],![]() k0
k0 ![]() Z.
Z.
![]()
![]() (x - a)g(x)dx =
(x - a)g(x)dx = ![]() [g(a-) + g(a+)].
[g(a-) + g(a+)].
![]() 0
0
![]()
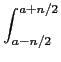 pn(x - a)g(x)dx
pn(x - a)g(x)dx![]()
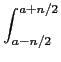 pn(x - a)dx
pn(x - a)dx![]() 0
0
![]() (x) = 0,
(x) = 0,
![]() (x) +
(x) + ![]() (x) = 0,
(x) = 0,
![]() (x) = -
(x) = - ![]() ,
,
![]() g(t)
g(t)![]() (t - a)dt
(t - a)dt![]() (- t)
(- t)![]() (t),
(t),![]() (at)
(at)![]() (t)/|a|,
(t)/|a|,![]() (- t)
(- t)![]() (t),
(t),![]()
![]() (a - t)
(a - t)![]() (t - b)dt
(t - b)dt![]() (a - b),
(a - b),![]() (t)
(t)![]() (t) + g(0)
(t) + g(0)![]() (t).
(t).![]() 0
0
![]()
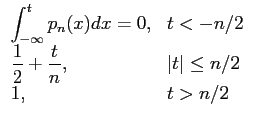
![]() 0
0
![]()
![]() (x)dx
(x)dx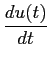 = u'(t) =
= u'(t) = ![]() (t).
(t).
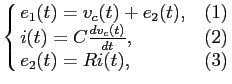
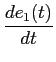 =
= 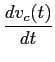 +
+ 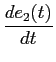
![]() = RC
= RC
![]() u(t),
u(t),
![]() u(t),
u(t),
![]() u(t),
u(t),
![]() u(t)
u(t)
![]() u(t) + 4e-(t-1)/
u(t) + 4e-(t-1)/![]() u(t - 1) + 6e-(t-2)/
u(t - 1) + 6e-(t-2)/![]() u(t - 2).
u(t - 2).![]() (t) + 4
(t) + 4![]() (t - 1) - 6
(t - 1) - 6![]() (t - 2)
(t - 2)
![]()
![]()
![]() < <
< < ![]()
![]()
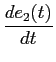 + e2(t)
+ e2(t)
![]() e-t/2u(t),
e-t/2u(t),
![]() = 2
= 2
![]() > > 0.2
> > 0.2
![]() = 10
= 10
![]() 10
10![]() (t)
(t)
![]() 5e-t/2u(t)
5e-t/2u(t)
![]()
![]()
![]()
![]()
![]() )
)
![]()
![]() )
)![]()
![]()
![]()
![]() < <
< < ![]()
![]()
![]() (t - n
(t - n![]() )
)
![]() )
)
![]()
![]() < <
< < ![]()
![]() [x(n
[x(n![]()
![]() )
)![]()
![]() ]
]![]() (t - n
(t - n![]()
![]() )
)![]()
![]() [x(n
[x(n![]()
![]() )
)![]()
![]() ]h(t - n
]h(t - n![]()
![]() ),
),
![]()
![]()
![]() 0
0
![]()
![]()
![]() d
d![]()
![]()
![]()
![]()
![]()
![]()
![]() nd
nd![]() =
= ![]()
![]() x(
x(![]() )
)![]() (t -
(t - ![]() )d
)d![]()
![]()
![]() x(
x(![]() )h(t -
)h(t - ![]() )d
)d![]() ,
,
![]() )
)![]() 0
0
![]()
![]() 0
0
![]()
![]() t
t
![]()
![]() (t - t0 -
(t - t0 - ![]() )x(
)x(![]() )d
)d![]() ,
,
![]() (t - t0),
(t - t0),
![]() x(
x(![]() )h(t -
)h(t - ![]() )d
)d![]()
![]()
![]()
![]() )
)
![]() )
)
![]() )
)
![]() )
)
![]() )
)
![]() )
)
![]() )
)
![]()
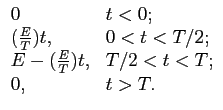
![]() )
)
![]()
![]() )
)
![]() (
(![]() )
)![]() h(t -
h(t - ![]() )d
)d![]() ,
,![]() (
(![]() )
)![]() h(t -
h(t - ![]() )d
)d![]() +
+ ![]() E(1 -
E(1 - ![]() )h(t -
)h(t - ![]() )d
)d![]() ,
,![]() (
(![]() )
)![]() h(t -
h(t - ![]() )d
)d![]() +
+ ![]() E(1 -
E(1 - ![]() )h(t -
)h(t - ![]() )d
)d![]() .
.![]()
![]()
![]() x(t -
x(t - ![]() )h(
)h(![]() )d
)d![]()
![]() = t -
= t - ![]()
![]() x(
x(![]() )h(t -
)h(t - ![]() )d
)d![]()
![]() x(
x(![]() )h(t -
)h(t - ![]() )d
)d![]()
![]() x(
x(![]() )h(t -
)h(t - ![]() )d
)d![]() ,
,
![]() =
= ![]() x(
x(![]() )
)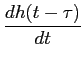 d
d![]() +
+ ![]()
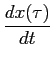 h(t -
h(t - ![]() )d
)d![]() ,
,
![]() )
)
![]() x(
x(![]() )h(1)(t -
)h(1)(t - ![]() )d
)d![]() =
= ![]() x(1)(t -
x(1)(t - ![]() )h(
)h(![]() )d
)d![]() ,
,
![]() h(
h(![]() )
)![]() (t -
(t - ![]() )d
)d![]() ,
,
![]() h(
h(![]() )u(t -
)u(t - ![]() )d
)d![]()
![]() h(
h(![]() )d
)d![]() .
.![]() (t)
(t)
![]() (t - t0)
(t - t0)
![]() h(
h(![]() )x(t -
)x(t - ![]() )d
)d![]() ,
,
![]() M <
M < ![]() ,
, ![]() t
t
![]() M
M![]() |h(
|h(![]() )|d
)|d![]() ,
, ![]() t
t
![]() x(
x(![]() )h(t -
)h(t - ![]() )d
)d![]() ,
,
![]() x(
x(![]() )h(t -
)h(t - ![]() )d
)d![]() ,
,
![]() (t) =
(t) = 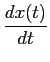 ,
,
![]() (t)
(t)
![]() (t),
(t),
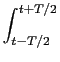 x(u)du,
x(u)du,
![]() 0
0
![]()
![]()
![]()
![]() ,
,![]() (t)/dt0 =
(t)/dt0 = ![]() (t)
(t)
![]()
![]()
![]() =
= ![]()
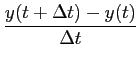 ,
,
![]() =
= ![$\displaystyle {{y[nT+T] - y[nT]}\over T}$](img124.png) ,
,
![]()
![]()
![]() 0
0
![]() 0
0
![]() hij(t) * xi(t), j = 1,..., J,
hij(t) * xi(t), j = 1,..., J,
![]()
![]() (t) =
(t) = ![]() (t)
(t) ![]()
![]() (t)
(t)![]()
![]() (t)
(t) ![]()
![]() (t).
(t).
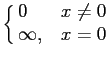
![$\displaystyle \begin{array}{ll}
\displaystyle{1/n,} & x \in [-n/2,n/2]\\
0, & {\rm outro}~x.
\end{array}$](img49.png)
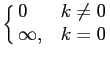 .
.
![\includegraphics[height=40mm,width=90mm]{figs/step-function.eps}](img59.png)
![\includegraphics[height=40mm,width=90mm]{figs/circuito-CR.eps}](img65.png)
![\includegraphics[height=50mm,width=100mm]{figs/circuito-RL.eps}](img75.png)
![\includegraphics[height=60mm,width=120mm]{figs/resp-circuito-RL.eps}](img76.png)
![\includegraphics[height=60mm]{figs/aprox-Dirac.eps}](img79.png)
![\includegraphics[height=200mm]{figs/convol-grafica.eps}](img92.png)
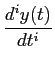 =
= 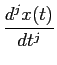 ,
,