



Next: Cálculo simbólico
Up: Aplicação aos sistemas lineares
Previous: Equações diferenciais com condições
Contents
Função de sistema
Podemos agora fazer uma generalização dos sistemas lineares de primeira e segunda ordem ao caso de uma ordem superior 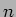 . Assim podemos dizer que a relação entre a entrada
. Assim podemos dizer que a relação entre a entrada 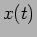 e a saída
e a saída 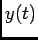 de um sistema linear pode ser descrita por uma equação do tipo1
de um sistema linear pode ser descrita por uma equação do tipo1
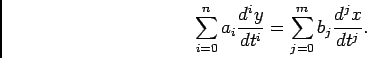 |
(4-3.03) |
Neste caso, e para condições iniciais nulas, temos que tomando a TL de ambos os termos,
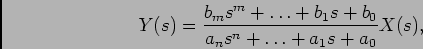 |
(4-3.04) |
daqui podemos deduzir a função de sistema, ou função de transferência, 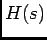 ,
,
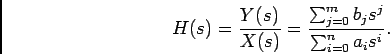 |
(4-3.05) |
No caso em que os pólos são todos simples, a função de transferência 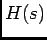 pode ser representada sob a forma de
pode ser representada sob a forma de
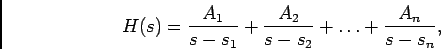 |
(4-3.06) |
então a sua TLI escreve-se
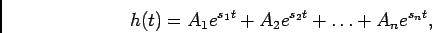 |
(4-3.07) |
que é chamada a resposta impulsiva do sistema, i.e., é a resposta do sistema 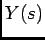 quando o sinal de entrada é um impulso de Dirac, e então visto que
quando o sinal de entrada é um impulso de Dirac, e então visto que
![${\rm TL}[x(t)=\delta(t)]=1$](img488.png) , temos que
, temos que 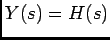 . Isto significa que a resposta impulsiva depende apenas da função de transferência
. Isto significa que a resposta impulsiva depende apenas da função de transferência 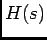 e por isso apenas do sistema ele mesmo e, em particular, dos pólos do sistema
e por isso apenas do sistema ele mesmo e, em particular, dos pólos do sistema
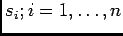 . Também isto não é estranho pois os pólos do sistema são aqueles que estão ligados à resposta natural do sistema, i.e., a resposta do sistema sem excitação - também chamada solução da equação homógenea.
. Também isto não é estranho pois os pólos do sistema são aqueles que estão ligados à resposta natural do sistema, i.e., a resposta do sistema sem excitação - também chamada solução da equação homógenea.
Exemplos:
A) sistema de primeira ordem sem condições iniciais: considere a figura 4.6, com 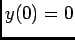 e
e
Figura 4.6:
sistema de primeira ordem.
|
|
Podemos directamente escrever
a partir da qual tiramos a TL
de onde a função do sistema 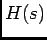 é
é
Desta podemos determinar a resposta impulsiva 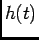 , que se escreve
, que se escreve
e sabendo que
portanto 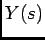 escreve-se
escreve-se
e finalmente
será a resposta do circuito no caso em que o sistema se encontra inerte no momento inicial, i.e., quando 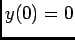 .
.
B) sistema de primeira ordem com condições iniciais: considere o mesmo sistema da figura 4.6 mas agora com um valor inicial da saída 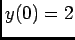 .
.
Não será necessário re-escrever todas as equações, mas sómente a TL da equação diferencial tendo em conta (4-2.29),
substituindo pelos valores númericos e pela transformada de 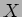 obtemos
obtemos
utlizando o resultado da decomposição do caso anterior, obtemos
onde simplificando
C) sistema de segunda ordem sem condições iniciais: considere agora o caso do sistema da figura 4.7 com
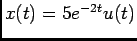 . Pretende-se calcular a saída
. Pretende-se calcular a saída 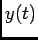 .
.
Figura 4.7:
sistema de segunda ordem.
|
|
Como anteriormente, podemos escrever directamente
cuja TL é dada por
visto que
![$X(s) = {\rm TL}[x(t)]$](img512.png) é dada por
é dada por
temos que, por substituição na equação anterior, e cálculo das raízes da equação do segundo grau do denominador
dando origem à representação no plano 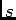 da figura 4.8. A inversão faz-se por decomposição da fração polinomial,
da figura 4.8. A inversão faz-se por decomposição da fração polinomial,
onde podemos fácilmente deduzir que
com
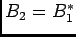 . Por questões de simplificação do cálculo é frequente colocar os coeficientes complexos sob forma exponencial. Assim podemos fácilmente escrever que
. Por questões de simplificação do cálculo é frequente colocar os coeficientes complexos sob forma exponencial. Assim podemos fácilmente escrever que
e portanto
Podemos agora calcular a TLI a cada um dos termos para obter
ou ainda simplificando
de onde deduzimos finalmente
Neste resultado final podemos fácilmente identificar que o primeiro termo - oscilação em 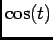 - é a resposta do sistema em regime permanente e o segundo - exponencial atenuada - é a resposta ao sinal de entrada
- é a resposta do sistema em regime permanente e o segundo - exponencial atenuada - é a resposta ao sinal de entrada 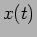 .
.
Figura 4.8:
pólos e zeros no plano 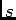 .
.
|
|




Next: Cálculo simbólico
Up: Aplicação aos sistemas lineares
Previous: Equações diferenciais com condições
Contents
Sergio Jesus
2003-12-07
![]() . Assim podemos dizer que a relação entre a entrada
. Assim podemos dizer que a relação entre a entrada ![]() e a saída
e a saída ![]() de um sistema linear pode ser descrita por uma equação do tipo1
de um sistema linear pode ser descrita por uma equação do tipo1
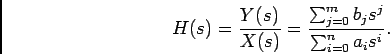
![]() e
e
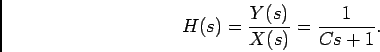
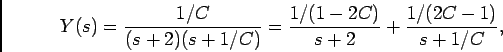
![]() .
.
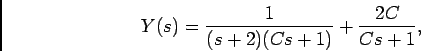
![]() . Pretende-se calcular a saída
. Pretende-se calcular a saída ![]() .
.
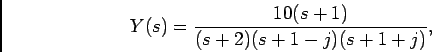
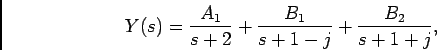
![\begin{displaymath}Y(s) = {{-5}\over {s+2}} + 5[{{e^{-j{\pi\over 4}}}\over {s+1-j}} + {{e^{j{\pi\over 4}}}\over {s+1+j}}].\end{displaymath}](img519.png)