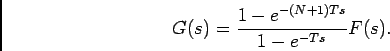Next: Transformada de Laplace Inversa
Up: Transformada de Laplace
Previous: Pólos e zeros duma
Contents
Na prática mais do que a própria definição, convém conhecer algumas das propriedades mais relavantes da TL, de modo a facilitar a sua aplicação à análise de circuitos.
Atraso no domínio temporal: o cálculo da TL de 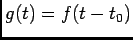 faz-se através de
faz-se através de
onde colocando 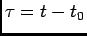 , e
, e 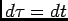 permite escrever
permite escrever
e de onde notando que a função causal 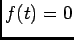 para
para 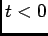 permite deduzir o resultado final
permite deduzir o resultado final
![\begin{displaymath}
{\rm TL}[f(t-t_0)] = e^{-t_0s} F(s).
\end{displaymath}](img386.png) |
(4-2.15) |
Diferenciação no domínio de Laplace:
demonstra-se fácilmente calculando a derivada de
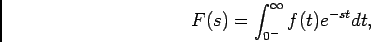 |
(4-2.16) |
em relação a 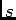 que é
que é
![\begin{displaymath}
G(s) = {{dF(s)}\over {ds}} = \int_{0^-}^{\infty} [-t f(t)] e^{-st} dt,
\end{displaymath}](img388.png) |
(4-2.17) |
e portanto temos o par
![\begin{displaymath}
{\rm TL}[t f(t)] = -{{dF(s)}\over {ds}}.
\end{displaymath}](img389.png) |
(4-2.18) |
e por dedução à ordem 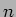
![\begin{displaymath}
{\rm TL} [(-t)^n f(t)] = {{d^n F(s)}\over {ds^n}}.
\end{displaymath}](img390.png) |
(4-2.19) |
Família de Diracs: a família de Diracs começa com o degrau unidade
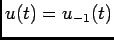 para o qual se pode fácilmente calcular
para o qual se pode fácilmente calcular
![\begin{displaymath}
{\rm TL}[u_{-1}(t)] = {1\over s},
\end{displaymath}](img392.png) |
(4-2.20) |
em seguida, utilizando (4-2.19)
![\begin{displaymath}
{\rm TL}[t^n u_{-1}(t)] = {{n!}\over {s^{n+1}}}.
\end{displaymath}](img393.png) |
(4-2.21) |
Podemos agora generalizar à família de impulsos com a ajuda de (4-2.19)
![\begin{displaymath}
{\rm TL}[u_{-n} (t)] = s^{-n}.
\end{displaymath}](img394.png) |
(4-2.22) |
Potência do tempo - função Gama: é um caso semelhante ao anterior no qual se pretende calcular a TL de uma potência do tempo, só que agora o expoente não é inteiro. Assim temos que
![\begin{displaymath}
{\rm TL}[t^{\alpha}] = {1\over {s^{\alpha+1}}} \int_{0^-}^{\...
...{\alpha} e^{-x} dx = {{\Gamma(\alpha+1)}\over {s^{\alpha+1}}},
\end{displaymath}](img395.png) |
(4-2.23) |
onde a função Gama é definida por
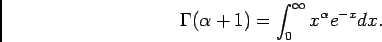 |
(4-2.24) |
Diferenciação temporal: pode-se demonstrar que
![\begin{displaymath}
{\rm TL}[{{df(t)}\over {dt}}] = sF(s) - f(0^-),
\end{displaymath}](img397.png) |
(4-2.25) |
onde 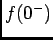 representa o valor da função temporal no instante inicial. A demonstração obtem-se fazendo
representa o valor da função temporal no instante inicial. A demonstração obtem-se fazendo
![\begin{displaymath}
G(s) = {\rm TL}[{{df(t)}\over {dt}}] = \int_{0^-}^{\infty} {{df(t)}\over {dt}} e^{-st}dt,
\end{displaymath}](img399.png) |
(4-2.26) |
de onde fazendo a mudança de variável 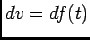 e
e 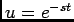 e integrando por partes,
e integrando por partes,
![\begin{displaymath}
G(s) = [e^{-st} f(t)]_{0^-}^{\infty} - \int_{0^-}^{\infty} f(t) [-se^{-st}], dt
\end{displaymath}](img402.png) |
(4-2.27) |
admitindo que 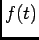 é de tipo exponencial temos que para o extremo superior (
é de tipo exponencial temos que para o extremo superior (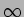 ) o primeiro termo dá zero e para
) o primeiro termo dá zero e para 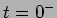 dá
dá 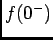 . Em relação ao segundo termo é fácil ver que se trata de
. Em relação ao segundo termo é fácil ver que se trata de 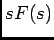 e por isso o resultado encontra-se como sendo
e por isso o resultado encontra-se como sendo
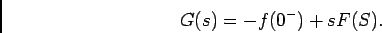 |
(4-2.28) |
As derivadas de ordem superior obtêm-se por extensão do caso precedente tal que
![\begin{displaymath}
{\rm TL}[{{d^n f(t)}\over {dt^n}}] = s^nF(S) -s^{n-1}f(0^-) - \ldots -f^{(n-1)}(0^-).
\end{displaymath}](img407.png) |
(4-2.29) |
Integração temporal: podemos ver facilmente que
![\begin{displaymath}
{\rm TL}[\int_{0^-}^t f(\tau) d\tau ] = {{F(s)}\over s},
\end{displaymath}](img408.png) |
(4-2.30) |
que se demonstra colocando
 |
(4-2.31) |
o que implica 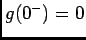 . Como podemos escrever que a
. Como podemos escrever que a
![${\rm TL}[dg(t)/dt]={\rm TL}[f(t)]=F(s)$](img411.png) , utilizando (4-2.28), podemos escrever que
, utilizando (4-2.28), podemos escrever que
![${\rm TL}[dg(t)/dt]=sG(s)-g(0^-)$](img412.png) . Assim, visto que
. Assim, visto que 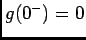 podemos escrever que
podemos escrever que 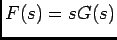 e finalmente provar (4-2.30).
e finalmente provar (4-2.30).
Teorema do valor inicial: prova-se que, para as funções sem descontinuidades na origem, podemos determinar o valor da função temporal para  através de
através de
 |
(4-2.32) |
Teorema do valor final: prova-se igualmente que o valor final da função temporal se pode determinar através de
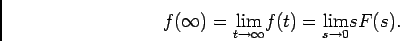 |
(4-2.33) |
Funções periódicas causais: é frequente na prática querermos determinar a TL de uma função periódica. Tomemos como exemplo o caso simples de uma função
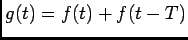 , resultante da repetição da função
, resultante da repetição da função 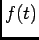 com um intervalo
com um intervalo 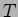 . Assim podemos directamente escrever
. Assim podemos directamente escrever
onde utilizámos (4-2.15). Ou ainda
![\begin{displaymath}
G(s) = F(s)[1+e^{-sT}].
\end{displaymath}](img418.png) |
(4-2.34) |
A partir deste caso simples deduzimos directamente o caso geral do sinal periódico causal onde se o sinal 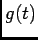 se escrever
se escrever
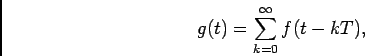 |
(4-2.35) |
então, a partir de (4-2.34), temos que
ou ainda, utilizando o desenvolvimento em série de 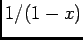 para
para
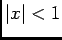 (ver A.2),
(ver A.2),
![\begin{displaymath}
G(s) = [{1\over {1-e^{-Ts}}}] F(s)
\end{displaymath}](img423.png) |
(4-2.36) |
Exemplo: queremos determinar a TL da função periódica causal e limitada no tempo dada por
A solução deste problema pode obter-se através da utilização de (4-2.36) tal que
onde a TL do segundo termo é uma soma de termos de uma progressão geométrica de razão 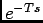 e cujo primeiro termo é
e cujo primeiro termo é 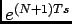 . Assim podemos escrever que
. Assim podemos escrever que
ou mais condensado
que é o resultado procurado.




Next: Transformada de Laplace Inversa
Up: Transformada de Laplace
Previous: Pólos e zeros duma
Contents
Sergio Jesus
2003-12-07
![]() faz-se através de
faz-se através de
![]() para o qual se pode fácilmente calcular
para o qual se pode fácilmente calcular
![]() através de
através de
![]() , resultante da repetição da função
, resultante da repetição da função ![]() com um intervalo
com um intervalo ![]() . Assim podemos directamente escrever
. Assim podemos directamente escrever
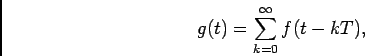
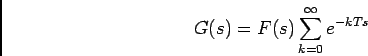
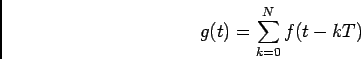
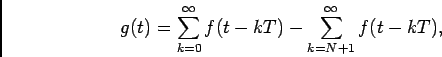
![\begin{displaymath}{\rm TL}[g(t)] = {{F(s)}\over {1-e^{-Ts}}} - {{F(s) e^{-(N+1)Ts}}\over {1-e^{-Ts}}}\end{displaymath}](img428.png)