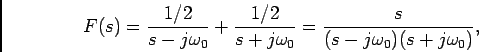Next: Teoremas simples da Transformada
Up: Transformada de Laplace
Previous: Definição e existência
Contents
Quase todas as funções de variável 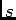 que consideraremos podem ser colocadas sob a forma de fração racional
que consideraremos podem ser colocadas sob a forma de fração racional
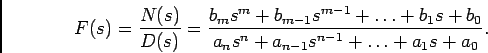 |
(4-2.13) |
De uma forma equivalente podemos exprimir os polinómios 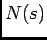 e
e 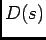 em função das suas raízes,
em função das suas raízes,
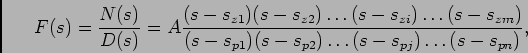 |
(4-2.14) |
onde 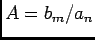 é uma constante. A partir de (4-2.14) podemos fácilmente determinar as valores de
é uma constante. A partir de (4-2.14) podemos fácilmente determinar as valores de 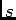 (em geral complexos) para as quais
(em geral complexos) para as quais 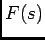 toma valores extremos, i.e., valores zero ou valores infinitos, consoante são raízes do numerador ou denominador, e são chamados pólos e zeros respectivamente.
toma valores extremos, i.e., valores zero ou valores infinitos, consoante são raízes do numerador ou denominador, e são chamados pólos e zeros respectivamente.
Figura 4.5:
localização de pólos e zeros no plano
complexo: um pólo real (a), dois pólos e um zero reais (b)
e dois pólos imaginários puros complexos conjugados (c).
|
|
Exemplos: vejamos alguns exemplos de TL e a sua representação no plano complexo com a respectiva localização de pólos e zeros.
A)
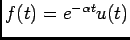
temos que
que tem apenas um pólo para 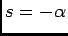 como representado na figura 4.5(a).
como representado na figura 4.5(a).
B)
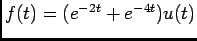
temos neste caso que
de onde utilizando o resultado anterior duas vezes com os devidos valores para 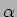 ,
,
com um zero em -3 e dois pólos: um em -4 e outro em -2, conforme representado na figura 4.5(b).
C)
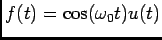
onde utilizando a forma de Euler,
e utilizando mais uma vez o resultado anterior
e neste caso teremos pólos complexos conjugados no eixo imaginário e um zero em 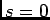 que se encontram representados na figura 4.5(c).
que se encontram representados na figura 4.5(c).




Next: Teoremas simples da Transformada
Up: Transformada de Laplace
Previous: Definição e existência
Contents
Sergio Jesus
2003-12-07
![]() que consideraremos podem ser colocadas sob a forma de fração racional
que consideraremos podem ser colocadas sob a forma de fração racional
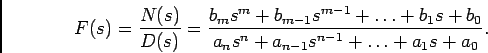
![\includegraphics[width=8cm]{figs/fig4-5.eps}](img366.png)
![]()
![\begin{displaymath}F(s) = \int_{0^-}^{\infty} e^{-\alpha t} e^{-st} dt = [{{e^{-...
...ha)t}}\over {-(s+\alpha)}}]_{0^-}^{\infty}={1\over {s+\alpha}},\end{displaymath}](img368.png)
![]()
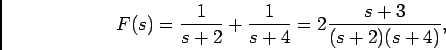
![]()