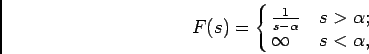Next: Pólos e zeros duma
Up: Transformada de Laplace
Previous: Transformada de Laplace
Contents
Começaremos pela sua definição no caso geral, que vem essencialmente da definição de Transformada de Fourier (TF), e que é
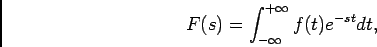 |
(4-2.06) |
que é denominada Transformada de Laplace (TL) bilateral, devido ao domínio de integração se estender de 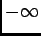 a
a 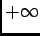 . Devido ao facto de, na prática, nos interessarmos quase exclusivamente pelas funções causais que são nulas apra
. Devido ao facto de, na prática, nos interessarmos quase exclusivamente pelas funções causais que são nulas apra 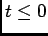 , seremos levados a utilizar mais frequentemente a TL unilateral que se escreve
, seremos levados a utilizar mais frequentemente a TL unilateral que se escreve
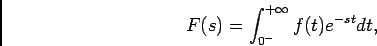 |
(4-2.07) |
na qual devemos no entanto precisar que o limite inferior deste integral inclui o ponto de origem do eixo do tempo; em particular, um impulso de Dirac na origem deverá ser tido em conta na TL. A transformada inversa é obtida, sempre através da analogia com a TF, por
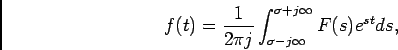 |
(4-2.08) |
onde, neste caso, o integral é de variável complexa.
Uma das questões mais importante no cálculo da TL é, antes de mais, a da sua existência. Já sabemos, a partir da TF, que a TL existe quando o integral de definição converge no intervalo considerado. Em geral utiliza-se a noção de convergência no sentido absoluto, i.e., que
 |
(4-2.09) |
que é uma noção mais exigente do que, se em vez de
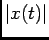 , utilizarmos apenas
, utilizarmos apenas 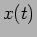 . Devido ao facto de que, em teoria de sinais, a maior parte das funções são de tipo exponencial para as quais
. Devido ao facto de que, em teoria de sinais, a maior parte das funções são de tipo exponencial para as quais
onde 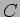 é uma constante real, coloca-se a questão de convergência para este tipo de funções, para as quais é importante relembrar a noção de abcissa de convergência absoluta. Podemos escrever (4-2.7) como
é uma constante real, coloca-se a questão de convergência para este tipo de funções, para as quais é importante relembrar a noção de abcissa de convergência absoluta. Podemos escrever (4-2.7) como
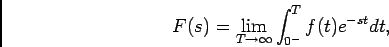 |
(4-2.10) |
podendo demonstrar-se que se a função 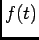 for de tipo exponencial (4-2.10) converge sempre, i.e., a sua TL existe. Além disso podemos também dizer em geral que
for de tipo exponencial (4-2.10) converge sempre, i.e., a sua TL existe. Além disso podemos também dizer em geral que
 |
(4-2.11) |
Trata-se aqui de determinar o domínio do plano 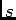 para o qual
para o qual 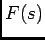 existe, de forma a podermos calcular a TL inversa. Para cada caso específico trata-se de calcular um valor
existe, de forma a podermos calcular a TL inversa. Para cada caso específico trata-se de calcular um valor 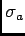 real tal que
real tal que
![\begin{displaymath}
Re [F(s)] > \sigma_a,
\end{displaymath}](img354.png) |
(4-2.12) |
neste caso 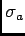 é chamada abcissa de convergência absoluta.
é chamada abcissa de convergência absoluta.
Exemplo: calcular a abcissa de convergência da função
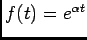 .
.
Temos então que
que se pode fácilmente calcular como sendo
e torna-se neste caso claro que 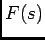 só existe (ou só toma valores finitos) para
só existe (ou só toma valores finitos) para 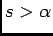 , i.e.,
, i.e.,
e por isso a abcissa de convergência absoluta é neste caso
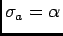 .
.




Next: Pólos e zeros duma
Up: Transformada de Laplace
Previous: Transformada de Laplace
Contents
Sergio Jesus
2003-12-07
![]() .
.