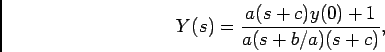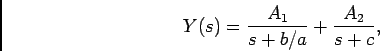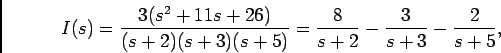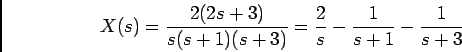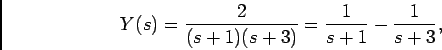Next: Função de sistema
Up: Aplicação aos sistemas lineares
Previous: Aplicação aos sistemas lineares
Contents
A utilização prática da TL na análise e síntese de sistemas lineares passa essencialmente pelas seguintes propriedades:
![\begin{displaymath}
{\rm TL}[\sum_i a_i f_i(t)] = \sum_i a_i F_i(s),
\end{displaymath}](img451.png) |
(4-3.01) |
e
![\begin{displaymath}
{\rm TL}[f^{(n)}(t)] = s^nF(s) -s^{n-1}f(0)- \ldots -s f^{(n-2)}(0) - f^{(n-1)}(0),
\end{displaymath}](img452.png) |
(4-3.02) |
com as quais as equações diferenciais em 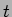 se tornam equações algébricas em
se tornam equações algébricas em 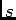 . Na prática o problema é quase sempre dividido em cinco etapas sucessivas:
. Na prática o problema é quase sempre dividido em cinco etapas sucessivas:
1) transformar a equação diferencial numa equação algébrica utilizando (4-3.2)
2) resolver a equação resultante para a grandeza de saída 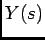
3) desenvolver 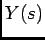 em frações racionais
em frações racionais
4) encontrar o inverso
![$y(t) = {\rm TLI} [Y(s)]$](img455.png)
5) verificar o resultado
Exemplos:
A) Seja a seguinte equação diferencial de primeira ordem
com
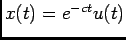 . Podemos desde já escrever a passagem para o domínio
. Podemos desde já escrever a passagem para o domínio 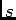 ,
,
isto é
ou também, decompondo em fracções racionais
com
e de onde se pode deduzir o resultado
A verificação do resultado faz-se, óbviamente, inserindo 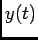 na equação diferencial inicial. Alternativamente poderíamos
utilizar os teoremas dos valores inicial e final, (4-2.32) e (4-2.33), respectivamente, para verificar o comportamento assimptótico da solução obtida.
na equação diferencial inicial. Alternativamente poderíamos
utilizar os teoremas dos valores inicial e final, (4-2.32) e (4-2.33), respectivamente, para verificar o comportamento assimptótico da solução obtida.
B) seja agora a equação diferencial de segunda ordem
com 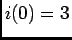 A e
A e 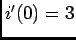 A/s. Podemos então escrever, calculando a TL de ambos os termos,
A/s. Podemos então escrever, calculando a TL de ambos os termos,
de onde, resolvendo em relação a 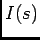 ,
,
e portanto a solução final
Na prática somos levados a considerar frequentemente, não uma equação única para determinar uma das variáveis do circuito, mas sim um conjunto de equações com várias variáveis, em geral ligadas entre elas, e por isso temos que colocar o problema sob a forma de um sistema de equações.
Exemplo: considere o seguinte sistema de equações diferenciais,
com condições iniciais nulas, i.e., 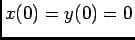 . Aplicando a TL nos dois membros de cada uma das equações acima obtemos,
. Aplicando a TL nos dois membros de cada uma das equações acima obtemos,
das quais podemos deduzir por substituição
e finalmente aplicando a TLI,
de onde podemos facilmente verificar as condições iniciais.




Next: Função de sistema
Up: Aplicação aos sistemas lineares
Previous: Aplicação aos sistemas lineares
Contents
Sergio Jesus
2003-12-07
![]()
![]() em frações racionais
em frações racionais
![]()