Subsections
Receptor óptimo em presença de ruído aditivo
Como já tivemos oportunidade de referir o filtro desmodulador no bloco receptor, constitui o elemento central do sistema de comunicações pois ele permite realizar, para além da colocação em banda base através de uma deslocação em frequência do sinal à saída do canal de transmissão, duas tarefas essenciais:
- eliminar, ou pelo menos diminuir, a ISI à entrada do amostrador e do decisor trabalhando em conjunto com o filtro emissor e a definição da ``função de pulso''.
- aumentar a relação sinal ruído à entrada do decisor e assim diminuir a probabilidade da escolha de um símbolo errado.
Já vimos igualmente que estas duas tarefas, apesar de não serem completamente contraditórias, necessitam o estabelecimento de um compromisso tendo em conta a complexidade prática dos sistema a implementar. O estudo aprofundado da igualização do canal de transmissão para a diminuição da ISI em canais de banda limitada vai ser deixado para a cadeira de Fundamentos de Telecomunicações II. Após a colocação do sinal em banda base, vamos abordar a questão da maximização da probabilidade de detecção à entrada do decisor assumindo que não existe ISI e que o canal é do tipo ruído aditivo Gaussiano e, nesse caso, vamos determinar qual o receptor óptimo. Veremos então que esse receptor óptimo pode ser implementado através do receptor-correlacionador ou filtro adaptado (matched filter).
Passagem em banda base
O primeiro bloco encontrado à entrada do receptor é o sistema de passagem do sinal recebido em banda base. Esta passagem em banda base é uma tarefa importante pois permite que todas as fases de processmento seguintes tenham lugar a uma velocidade de processamento muito mais baixa, o que trás uma economia de custos e de consumos a todos os níveis. A figura 8.1 mostra três formas clássicas de passagem do sinal recebido em banda base. Na figura 8.1(a) o sinal recebido y(t)
mathend000# é primeiramente filtrado com um filtro passa-banda resultando daí um sinal com duas bandas em torno a 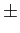 fc
mathend000# e tem por objectivo eliminar sinais e ruídos que possam existir noutras bandas de frequ
fc
mathend000# e tem por objectivo eliminar sinais e ruídos que possam existir noutras bandas de frequ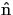 cia. O bloco seguinte é um phase splitter que, como já foi dito anteriormente, tem por função cortar a parte negativa do espectro sendo que o multiplicador a seguir tem por função fazer o deslocamento em frequência de forma a deslocar o espectro de + fc
mathend000# para zero Hz. Na esquema (b) da mesma figura utiliza-se filtro passa-banda analítico que é o mesmo que dizer, um filtro passa-banda com apenas uma das bandas em torno a mais ou menos fc
mathend000#. Obviamente que este filtro passa-banda analítico é sempre seguido por um multiplicador para efectuar a translação em frequência de fc
mathend000# para zero Hz. Finalmente no esquema (c) utiliza-se uma forma alternativa às anteriores, na qual primeiro o sinal é deslocado de - fc
mathend000# Hz através do multiplicador e só depois é filtrado por um filtro passa-baixo. Este conjunto de operações encontra-se representado de forma esquematizada na figura 8.2. Esta última implementação tem a vantagem de permitir uma execução do filtro mais simples, por este se encontrar já no sinal em banda-base.
cia. O bloco seguinte é um phase splitter que, como já foi dito anteriormente, tem por função cortar a parte negativa do espectro sendo que o multiplicador a seguir tem por função fazer o deslocamento em frequência de forma a deslocar o espectro de + fc
mathend000# para zero Hz. Na esquema (b) da mesma figura utiliza-se filtro passa-banda analítico que é o mesmo que dizer, um filtro passa-banda com apenas uma das bandas em torno a mais ou menos fc
mathend000#. Obviamente que este filtro passa-banda analítico é sempre seguido por um multiplicador para efectuar a translação em frequência de fc
mathend000# para zero Hz. Finalmente no esquema (c) utiliza-se uma forma alternativa às anteriores, na qual primeiro o sinal é deslocado de - fc
mathend000# Hz através do multiplicador e só depois é filtrado por um filtro passa-baixo. Este conjunto de operações encontra-se representado de forma esquematizada na figura 8.2. Esta última implementação tem a vantagem de permitir uma execução do filtro mais simples, por este se encontrar já no sinal em banda-base.
Figura 8.1:
sistema de passagem em banda base: filtro passa banda -> splitter -> multiplicador (a), filtro-splitter -> multiplicador (b) e multiplicador -> filtro passa baixo (c).
|
|
Na prática, se o filtro receptor tiver uma resposta impulsiva f (t)
mathend000# contido na banda [- W, W]
mathend000#, então o filtro passa-banda deverá tmbém deixar passar uma banda
|f|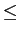 W
mathend000# em torno a
W
mathend000# em torno a 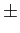 fc
mathend000#. No caso da figura 8.1(b) o filtro e o phase splitter são agrupados num só bloco resultando num filtro passa banda (chamado filtro passa-banda analítico) de resposta impulsiva (complexa)
fc
mathend000#. No caso da figura 8.1(b) o filtro e o phase splitter são agrupados num só bloco resultando num filtro passa banda (chamado filtro passa-banda analítico) de resposta impulsiva (complexa)
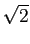 f (t)e-j2 f (t)e-j2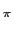 fct fct |
(8-1.01) |
que só deixa passar as frequências positivas. Pode-se facilmente provar que a estrutura (c) é equivalente às precedentes usando por exemplo a comparação entre (c) e (b), e notando que
e-j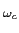 t t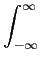 y( y( ) )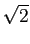 f (t- f (t- )ej2 )ej2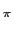 fc(t- fc(t-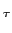 )d )d |
= 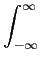 y( y( )e-j2 )e-j2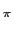 fc fc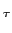 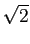 f (t- f (t- )d )d |
| |
= (e-j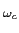 ty(t)) * ( ty(t)) * (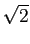 f (t)). f (t)). |
|
(8-1.02) |
Figura 8.2:
operação de pasagem em banda base de um sinal PM seguida de filtragem passa-baixo (caso (c) da figura 8.1).
|
|
Até agora apenas temos focado o problema da desmodulação. O sinal obtido depois de passagem em banda base necessita igualmente de filtragem obtendo-se sempre um sinal em banda base. Assume-se que a partir daqui teremos um sistema como o da figura 7.1., composto de um amostrador, de um decisor e de um descodificador até recuperar uma estimativa da trama de bits transmitida. Porém existe uma diferença fundamental decorrente do sistema de modulação/desmodulação que é o facto de que o sinal em banda de base que sai do desmodulador é agora complexo enquanto à partida (no emissor) era real. Este facto irá necessitar no mínimo um amostrador/decisor/descodificador complexo ou então uma separação em quadratura para implementar separadamente a parte real e a parte imaginária.
Para além desta existe uma outra questão que é a do ruído. Vejamos o que se passa à saída Z(t)
mathend000# de um filtro/desmodulador se aplicarmos à entrada um ruído branco e Gaussiano de densidade espectral
SN( ) = N0/2
mathend000#. Consideremos, a título de exemplo, a estrutura da figura 8.1b. A densidade espectral da saída do filtro analítico passa banda é
) = N0/2
mathend000#. Consideremos, a título de exemplo, a estrutura da figura 8.1b. A densidade espectral da saída do filtro analítico passa banda é
SM(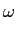 ) = N0|F( ) = N0|F(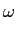 - - 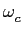 ) )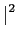 |
(8-1.03) |
e em seguida a passagem em banda base implica que
SZ(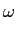 ) = SM( ) = SM(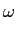 + + 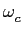 ) = N0|F( ) = N0|F(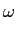 ) )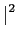 , , |
(8-1.04) |
expressão que mais uma vez sugere a diminuição da largura de banda do filtro de recepção para minimizar a potência do ruído na saída.
Equivalente em banda base
Finalmente poderemos dar uma representação equivalente em banda base do transmissor/canal/receptor incluindo a parte de modulação/desmodulação.
Figura 8.3:
esquema bloco do sistema equivalente em banda base. Z(t)
mathend000# é o ruído n(t)
mathend000# depois de filtrado pelo receptor e colocado em banda base.
|
|
Este canal equivalente encontra-se representado na figura 8.3 onde ak
mathend000# é a trama de símbolos (complexa) e p(t)
mathend000# é o sinal à saída do filtro de recepção sendo todo o bloco emissor/canal/receptor representado por
P(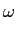 ) = G( ) = G(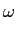 )B( )B(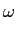 + + 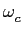 )F( )F(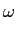 ), ), |
(8-2.01) |
que é uma expressão semelhante ao equivalente banda base já encontrado anteriormente, só com a diferença que agora temos
B( +
+ 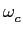 )
mathend000# em vez de B(
)
mathend000# em vez de B( )
mathend000# para indicar que se trata das propriedades do canal em torno a
)
mathend000# para indicar que se trata das propriedades do canal em torno a 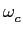 mathend000# e não em banda base e também é preciso notar que as TF-1
mathend000# das quantidades aqui representadas não são necessariamente funções reais e até na grande maioria dos casos, serão mesmo complexas. Como anteriormente, de forma a evitar/eliminar a ISI, deveremos escolher o filtro de recepção F(
mathend000# e não em banda base e também é preciso notar que as TF-1
mathend000# das quantidades aqui representadas não são necessariamente funções reais e até na grande maioria dos casos, serão mesmo complexas. Como anteriormente, de forma a evitar/eliminar a ISI, deveremos escolher o filtro de recepção F( )
mathend000# tal que
)
mathend000# tal que
F(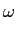 ) = ) =  |
(8-2.02) |
como anteriormente F( )
mathend000# terá um ganho elevado para frequências com fracos valores de
B(
)
mathend000# terá um ganho elevado para frequências com fracos valores de
B( +
+ 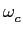 )G(
)G( )
mathend000#, amplificando o ruído.
)
mathend000#, amplificando o ruído.
Será útil determinar a representação discreta equivalente ao total do sistema de comunicação PM em banda passante, eventualmente utilizando a representação em banda base equivalente ao bloco transmissor/canal/receptor (figura 8.3). Esta representação discreta equivalente encontra-se na figura 8.4 que se abstrai de toda a parte modulação/desmodulação incluindo-a num único bloco de entrada Ak
mathend000# e saída pk = p(kT)
mathend000#
Figura 8.4:
sistema PAM em banda passante: equivalente discreto.
|
|
Um receptor simples amostra o sinal à taxa de transmissão (assumida síncrona com o emissor, para simplificar) e compara as amostras obtidas com um nível e, a partir daí,
mathend000#decide qual dos símbolos se encontra presente. Este receptor simples é geralmente longe do óptimo porque ignora o filtro f (t)
mathend000#, que deverá ser usado para filtrar as componentes fora da banda do canal de transmissão de forma a minimizar o ruído à entrada do amostrador/decisor. Assim f (t)
mathend000# (e de alguma forma também g(t)
mathend000#) tem um duplo objectivo: por um lado deverá assegurar uma forma de p(t)
mathend000# que satisfaça ''razoavelmente'' o critério de Nyquist e que assegure uma ISI nula (ou baixa) e por outro lado que minimize a taxa de ruído. Estes dois objectivos nem sempre (ou quase nunca) podem ser atingidos a 100% e por vezes o tentar manter uma complexidade aceitável limita o desempenho de f (t)
mathend000# de forma a tornar-se necessário encontrar um compromisso entre ISI e relação sinal/ruído à entrada do decisor. O problema coloca-se frequentemente em termos da dupla minimização do ruído e da ISI ou, alternativamente, na minimização do ruído mantendo uma ISI a um nível aceitável.
Podemos então escrever para o sinal p(t)
mathend000# à saída do filtro receptor
P(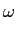 ) = F( ) = F(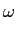 )B( )B(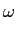 )G( )G(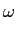 ), ), |
(8-2.03) |
e portanto temos que para o filtro F( )
mathend000#
)
mathend000#
F(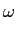 ) = ) =  |
(8-2.04) |
O facto de forçar F( )
mathend000# a zero para toda uma gama de frequências não é restritivo pois nessa mesma gama de frequências
B(
)
mathend000# a zero para toda uma gama de frequências não é restritivo pois nessa mesma gama de frequências
B( )G(
)G( ) = 0
mathend000# o que quer dizer que o sinal à saída seria zero de qualquer forma. Geralmente a forma de G(
) = 0
mathend000# o que quer dizer que o sinal à saída seria zero de qualquer forma. Geralmente a forma de G( )
mathend000# é determinada por questões de custo e por isso F(
)
mathend000# é determinada por questões de custo e por isso F( )
mathend000# desempenhará todo o papel na filtragem do ruído e na minimização da ISI. Mais à frente estudaremos quais as implicações do ruído na taxa de erro do decisor, por enquanto não ficaremos surprendidos se admitirmos que a taxa de erro cresce monotonamente com a diminuição da relação sinal/ruído. Retomando a expressão (7-4.29) do sinal q(t)
mathend000# à saída do filtro temos que no caso com ISI nula no qual
)
mathend000# desempenhará todo o papel na filtragem do ruído e na minimização da ISI. Mais à frente estudaremos quais as implicações do ruído na taxa de erro do decisor, por enquanto não ficaremos surprendidos se admitirmos que a taxa de erro cresce monotonamente com a diminuição da relação sinal/ruído. Retomando a expressão (7-4.29) do sinal q(t)
mathend000# à saída do filtro temos que no caso com ISI nula no qual
onde Ak
mathend000# é a amostra desejada e uk
mathend000# é o ruído
u(t) = f (t)*n(t)
mathend000# filtrado e discretizado, de variância
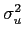 mathend000#. Assim podemos escrever a SNR à saída do filtro
mathend000#. Assim podemos escrever a SNR à saída do filtro
SNR = ![$\displaystyle {{E[\vert A_k \vert^2]}\over {\sigma_u^2}}$](img489.png) . . |
(8-2.06) |
É corrente assumir que os símbolos se encontram normalizados, de tal forma que
E[|Ak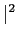 ] = 1
mathend000# e por isso temos que
] = 1
mathend000# e por isso temos que
SNR = 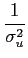 . . |
(8-2.07) |
Em resumo, podemos dizer que, tendo fixado a forma do pulso G( )
mathend000#, por um lado F(
)
mathend000#, por um lado F( )
mathend000# terá que compensar (igualizar) o canal B(
)
mathend000# terá que compensar (igualizar) o canal B( )
mathend000#, segundo (8-2.4), e por outro terá que diminuir a variância do ruído à sua saída, segundo (8-2.7), de forma a aumentar a relação SNR e assim diminuir a taxa de erro. Como já dissemos estes dois objectivos podem ser contraditórios, o que se pode facilmente perceber, por exemplo, para valores de
)
mathend000#, segundo (8-2.4), e por outro terá que diminuir a variância do ruído à sua saída, segundo (8-2.7), de forma a aumentar a relação SNR e assim diminuir a taxa de erro. Como já dissemos estes dois objectivos podem ser contraditórios, o que se pode facilmente perceber, por exemplo, para valores de  mathend000# nos quais
B(
mathend000# nos quais
B( )G(
)G( )
mathend000# tenha valores próximos de 0, e assim F(
)
mathend000# tenha valores próximos de 0, e assim F( )
mathend000# tome valores muito elevados para os quais o ruído se encontrará fortemente amplificado à saída aumentando assim a probabilidade de erro. O compromisso ISI vs. SNR é um eterno quebra-cabeças no desenho de equalizadores. Em FTEL II estudaremos um tipo de igualizadores chamado igualizador de Viterbi, para o qual se demonstra que permite minimizar, ou por vezes eliminar, esta amplificação do ruído. Este tipo de igualizadores são altamente não lineares.
)
mathend000# tome valores muito elevados para os quais o ruído se encontrará fortemente amplificado à saída aumentando assim a probabilidade de erro. O compromisso ISI vs. SNR é um eterno quebra-cabeças no desenho de equalizadores. Em FTEL II estudaremos um tipo de igualizadores chamado igualizador de Viterbi, para o qual se demonstra que permite minimizar, ou por vezes eliminar, esta amplificação do ruído. Este tipo de igualizadores são altamente não lineares.
Tendo em conta o que foi dito nos últimos capítulos poderemos agora introduzir um novo modelo equivalente ao sistema da figura 7.1 no qual o filtro de transmissão, canal e filtro de recepção se encontram juntos num único bloco caracterizado através da sua entrada, a sequência de símbolos Ak
mathend000# e da sua saída pk
mathend000#. Este novo modelo equivalente encontra-se representado na figura 8.5. De notar que visto que tanto a entrada como a saída deste novo filtro são discretos, todo o modelo passa a ser completamente discreto, tanto que
| pk = p(kT) = [g(t) * b(t) * f (t)]t=kT, |
(8-2.08) |
e a sequência de ruído filtrado (não branco)
| uk = u(kT) = [n(t) * f (t)]t=kT. |
(8-2.09) |
Figura 8.5:
sistema discreto equivalente ao sistema PAM em banda base.
|
|
O receptor óptimo
Como já foi dito acima, supôr que o sistema não tem ISI é equivalente a supôr que cada pulso (por exemplo num sistema de modulação PM) é recebido isoladamente e não tem relação com o seguintes, numa palavra, trata-se de um sistema sem memória. De um modo geral o que se pretende é que dado um determinado sinal recebido
| r(t) = sm(t) + w(t), |
(8-3.01) |
onde w(t)
mathend000# é o ruído assumido branco, estacionário, Gaussiano de média nula e de variância
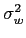 mathend000#, e cuja versão discreta num determinado intervalo de tempo pode ser escrita sob forma vectorial
mathend000#, e cuja versão discreta num determinado intervalo de tempo pode ser escrita sob forma vectorial
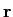 =
=  +
+ 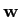 mathend000#7, a probabilidade que seja tomada a decisão correcta, de que o sinal sm(t)
mathend000# se encontra presente, seja máxima. Vamos notar essa probabilidade como
P[
mathend000#7, a probabilidade que seja tomada a decisão correcta, de que o sinal sm(t)
mathend000# se encontra presente, seja máxima. Vamos notar essa probabilidade como
P[ |
|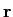 ]
mathend000# que, por palavras é a probabilidade condicional para que o sinal
]
mathend000# que, por palavras é a probabilidade condicional para que o sinal  mathend000# seja escolhido quando o sinal
mathend000# seja escolhido quando o sinal 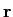 mathend000# é observado sabendo que
mathend000# é observado sabendo que  mathend000# foi emitido. Esta probabilidade é normalmente designada por probabilidade à posteriori. O critério que consiste em maximizar a probabilidade à posteriori (e que veremos corresponde a minimizar a probabilidade de erro) é denomidado o maximum a posteriori probability (MAP) criterium. Utilizando a lei de Bayes podemos escrever
mathend000# foi emitido. Esta probabilidade é normalmente designada por probabilidade à posteriori. O critério que consiste em maximizar a probabilidade à posteriori (e que veremos corresponde a minimizar a probabilidade de erro) é denomidado o maximum a posteriori probability (MAP) criterium. Utilizando a lei de Bayes podemos escrever
onde
P[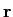 |
| ]
mathend000# é a probabilidade condicional de receber a sequência
]
mathend000# é a probabilidade condicional de receber a sequência 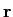 mathend000# condicionada no sinal
mathend000# condicionada no sinal  mathend000#. Por oposição,
P[
mathend000#. Por oposição,
P[ ]
mathend000# que é a probabilidade do sinal sm(t)
mathend000#, é normalmente denominada probabilidade à priori. A resolução do problema requer o conhecimento da probabilidade à priori
P[
]
mathend000# que é a probabilidade do sinal sm(t)
mathend000#, é normalmente denominada probabilidade à priori. A resolução do problema requer o conhecimento da probabilidade à priori
P[ ]
mathend000#. No caso de sinais equiprováveis (frequente na prática), onde
P[
]
mathend000#. No caso de sinais equiprováveis (frequente na prática), onde
P[ ] = 1/M;m = 1,..., M
mathend000#, substituindo em (8-3.2) permite obter
] = 1/M;m = 1,..., M
mathend000#, substituindo em (8-3.2) permite obter
de onde se vê que o problema de encontrar  mathend000# que maximiza a probabilidade à posteriori é idêntico ao de maximizar a densidade de probabilidade condicional
P[
mathend000# que maximiza a probabilidade à posteriori é idêntico ao de maximizar a densidade de probabilidade condicional
P[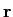 |
| ]
mathend000#, dado que
P[
]
mathend000#, dado que
P[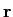 ]
mathend000# não depende de
]
mathend000# não depende de  mathend000#. É interessante verificar que o critério MAP conduz à maximização da mesma densidade de probabilidade do máximo de verosímilhança, neste sentido
P[
mathend000#. É interessante verificar que o critério MAP conduz à maximização da mesma densidade de probabilidade do máximo de verosímilhança, neste sentido
P[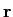 |
| ]
mathend000# é denominada função de verosímilhança (ou likelihood function). A maximização da função de verosimilhança conduz ao critério de máxima verosímilhança (maximum likelihood (ML) criterion). Neste caso, no qual os sinais
]
mathend000# é denominada função de verosímilhança (ou likelihood function). A maximização da função de verosimilhança conduz ao critério de máxima verosímilhança (maximum likelihood (ML) criterion). Neste caso, no qual os sinais  mathend000# são equiprováveis, os critérios MAP e ML conduzem ao mesmo resultado. Considerando que o ruído aditivo introduzido pelo canal segue uma distribuição gaussiana, podemos notar que cada amostra rk
mathend000# do sinal r(t)
mathend000# tem média smk
mathend000# dado que o ruído é de média nula. Assim a probabilidade da amostra recebida no instante k
mathend000# escreve-se8 como a densidade de probabilidade marginal
mathend000# são equiprováveis, os critérios MAP e ML conduzem ao mesmo resultado. Considerando que o ruído aditivo introduzido pelo canal segue uma distribuição gaussiana, podemos notar que cada amostra rk
mathend000# do sinal r(t)
mathend000# tem média smk
mathend000# dado que o ruído é de média nula. Assim a probabilidade da amostra recebida no instante k
mathend000# escreve-se8 como a densidade de probabilidade marginal
P[rk] = 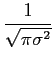 exp exp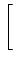 - - 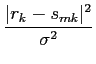 ![$\displaystyle \left.\vphantom{- {{\vert r_k-s_{mk}\vert^2}\over {\sigma^2}} }\right]$](img501.png) , m = 1,..., M , m = 1,..., M |
(8-3.04) |
onde
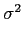 = 2
= 2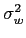 mathend000#. Notando que
mathend000#. Notando que 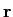 mathend000# é formado por N
mathend000# amostras não correlacionadas, podemos escrever a densidade de probabilidade conjunta do vector
mathend000# é formado por N
mathend000# amostras não correlacionadas, podemos escrever a densidade de probabilidade conjunta do vector 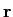 mathend000# como o produto das densidades de probabilidade marginais,
mathend000# como o produto das densidades de probabilidade marginais,
P[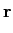 | |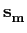 ] ] |
= |
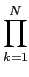 P[rk] P[rk] |
|
| |
= |
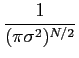 exp exp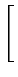 - - 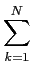 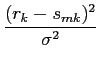 ![$\displaystyle \left.\vphantom{- \sum_{k=1}^N {{(r_k-s_{mk})^2}\over {\sigma^2}} }\right]$](img507.png) , m = 1,..., M , m = 1,..., M |
(8-3.05) |
A partir deste ponto torna-se conveniente escrever a função de verosímilhança utilizando uma função monótona da densidade de probabilidade como por exemplo o logaritmo. O logaritmo de (8-3.5) é frequentemente chamada log-likelihood function) e é uma forma clássica de ultrapassar o problema colocado pela maximização da exponencial. A partir da equação precedente temos que o log da função de verosímilhança se pode escrever
log P[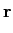 | |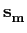 ] ] |
= |
- 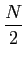 ( (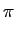 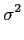 ) - ) - 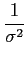 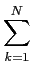 (rk-smk)2, m = 1,..., M (rk-smk)2, m = 1,..., M |
|
| |
= |
- 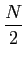 ( (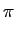 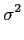 ) - ) - 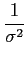 | |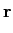 - - 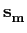 |2, m = 1,..., M |2, m = 1,..., M |
(8-3.06) |
onde foi utilizado o facto de que a norma de um vector, isto é, o seu comprimento é simplesmente igual à soma dos quadrados das suas coordenadas.
No segundo membro de (8-3.6) o primeiro termo é constante, independente de  mathend000# e pode ser descartado. A maximização da expressão em relação a
mathend000# e pode ser descartado. A maximização da expressão em relação a  mathend000#, é equivalente à minimização do segundo termo, por causa do sinal - antes do somatório. Este segundo termo escreve-se (deprezando a constante multiplicativa),
mathend000#, é equivalente à minimização do segundo termo, por causa do sinal - antes do somatório. Este segundo termo escreve-se (deprezando a constante multiplicativa),
C(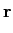 , ,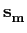 ) ) |
= |
|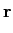 - - 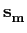 |2 m = 1,..., M |2 m = 1,..., M |
|
| |
= |
|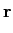 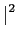 -2 -2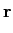 . . 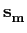 +| +|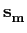 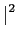 , m = 1,..., M , m = 1,..., M |
(8-3.07) |
sendo que o primeiro termo do segundo membro também não depende de  mathend000# e mais uma vez a minimização de
C(
mathend000# e mais uma vez a minimização de
C(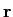 ,
, )
mathend000# é equivalente à maximização de
C'(
)
mathend000# é equivalente à maximização de
C'(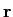 ,
, )
mathend000# dada por
)
mathend000# dada por
C'(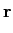 , ,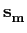 ) = 2 ) = 2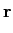 . . 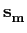 -| -|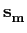 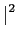 , m = 1,..., M , m = 1,..., M |
(8-3.08) |
onde
{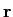 .
.  ;m = 1,..., M}
mathend000# é o produto escalar entre os dois vectores
;m = 1,..., M}
mathend000# é o produto escalar entre os dois vectores 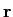 mathend000# e
mathend000# e  mathend000# para todos os valores de m
mathend000# ou, por outras palavras, a projecção de
mathend000# para todos os valores de m
mathend000# ou, por outras palavras, a projecção de 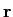 mathend000# no sub espaço vectorial gerado pelos vectores
{
mathend000# no sub espaço vectorial gerado pelos vectores
{ ;m = 1,..., M}
mathend000# e onde o segundo termo
|
;m = 1,..., M}
mathend000# e onde o segundo termo
|
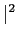 mathend000# representa a energia contida em cada um dos sinais sm(t)
mathend000#. O valor de cada uma destas projecções pode ser visto como a correlação entre o sinal recebido r(t)
mathend000# e cada um dos possíveis sinais emitidos sm(t)
mathend000#, e assim C'
mathend000# pode ser dado por um (chamado) receptor-correlacionador
mathend000# representa a energia contida em cada um dos sinais sm(t)
mathend000#. O valor de cada uma destas projecções pode ser visto como a correlação entre o sinal recebido r(t)
mathend000# e cada um dos possíveis sinais emitidos sm(t)
mathend000#, e assim C'
mathend000# pode ser dado por um (chamado) receptor-correlacionador
C'(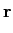 , ,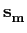 ) = 2 ) = 2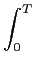 r(t)sm(t)dt - r(t)sm(t)dt - 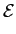 m m = 1,..., M m m = 1,..., M |
(8-3.09) |
onde a função de correlação é calculada para o ponto 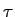 = 0
mathend000# e em seguida é selecionado o sinal sm
mathend000# para o qual
C(
= 0
mathend000# e em seguida é selecionado o sinal sm
mathend000# para o qual
C(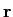 ,
, )
mathend000# é máximo. O receptor óptimo correspondente encontra-se representado na figura 8.6.
)
mathend000# é máximo. O receptor óptimo correspondente encontra-se representado na figura 8.6.
Figura 8.6:
receptor correlacionador para M
mathend000# sinais
{sm(t);m = 1,..., M}
mathend000#.
|
|
O filtro adaptado como receptor óptimo
A maximização da relação sinal/ruído à saída de um filtro é um problema clássico em teoria do sinal e pode ser transposto para o caso da recepção de mensagens num sistema de comunicações considerando primeiramente que: o sistema se encontra em banda base (ou seu equivalente) e que apenas um símbolo é transmitido, o que significa que não existe ISI. O sinal recebido pode ser então
| y(t) = A0h(t) + n(t), |
(8-4.01) |
onde A0
mathend000# é o símbolo transmitido, h(t)
mathend000# é a forma de pulso depois de passada no canal e n(t)
mathend000# é o ruído suposto aditivo branco e Gaussiano. Neste caso o sinal à saída do filtro de recepção de resposta impulsiva f (t)
mathend000# escreve-se
q(t) = 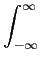 y( y( )f (t - )f (t -  )d )d . . |
(8-4.02) |
O sinal q(t)
mathend000# encontra-se depois amostrado ao instante t = 0
mathend000# (para retirar o símbolo A0
mathend000#) e então
Q0 = 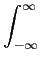 y( y( )f (- )f (-  )d )d . . |
(8-4.03) |
Substituindo agora (8-4.1) em (8-4.3) temos
Q0 = A0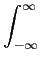 h( h( )f (- )f (-  )d )d + + 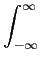 n( n( )f (- )f (-  )d )d , , |
(8-4.04) |
na qual o primeiro termo corresponde ao sinal e o segundo corresponde ao ruído. Intuitivamente o desempenho do nosso decisor será tanto melhor quanto maior for o primeiro termo em relação ao segundo, i.e., quanto maior for a relação SNR à saída do filtro9. Esta relação SNR escreve-se
| SNRout |
= |
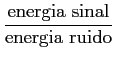 , , |
|
| |
= |
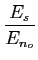 , , |
(8-4.05) |
onde ambas as energias são medidas à saída do filtro. A energia do sinal Es
mathend000# é dada pelo valor esperado do primeiro termo de do segundo membro de (8-4.4), i.e.,
| Es |
= |
E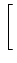 A0 A0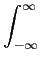 h( h( )f (- )f (-  )d )d ![$\displaystyle \left.\vphantom{A_0\int_{-\infty}^{\infty} h(\tau) f(-\tau) d\tau}\right]$](img514.png) |
|
| |
= |
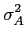 | |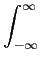 h( h( )f (- )f (-  )d )d 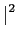 , , |
(8-4.06) |
enquanto a energia do ruído (suposto estacionário e ergódico) à saída do filtro, Eno
mathend000#, é dada pelo valor da função de autocorrelação no ponto 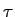 = 0
mathend000# por (2-3.12) onde a densidade espectral de potência é dada segundo (2-3.18) por
= 0
mathend000# por (2-3.12) onde a densidade espectral de potência é dada segundo (2-3.18) por
Pno(f )=|F(f )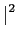 Pn(f ) Pn(f ) |
(8-4.07) |
e assim a energia do ruído de saída escreve-se
Eno = E[n02] = < n02 > = 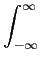 |F(f ) |F(f )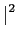 Pn(f )df, Pn(f )df, |
(8-4.08) |
onde < . >
mathend000# indica média temporal e onde o ruído branco
Pn(f )= cte = N0
mathend000# e por isso, utilizando de novo o teorema de Parseval
Substituindo (8-4.6) e (8-4.9) em (8-4.5) o problema agora é determinar de forma única o filtro f (t)
mathend000# que maximize
SNRout = 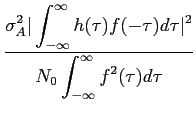 . . |
(8-4.10) |
A demonstração mais simples passa pela utilização da desigualdade de Schwartz que diz que
|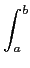 g1(x)g2(x)dx g1(x)g2(x)dx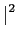 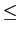 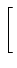 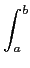 |g1(x) |g1(x)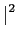 dx dx![$\displaystyle \left.\vphantom{ \int_a^b \vert g_1(x)\vert^2 dx }\right]$](img517.png) 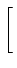 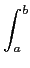 |g2(x) |g2(x)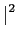 dx dx![$\displaystyle \left.\vphantom{ \int_a^b \vert g_2(x)\vert^2 dx }\right]$](img519.png) , , |
(8-4.11) |
onde a igualdade só é verificada quando
g2(x) = Kg1(x)
mathend000#, K
mathend000# constante. Portanto, utilizando (8-4.11) no numerador de (8-4.10) chegamos à conclusão que
onde a igualdade só é verificada (e por isso o valor máximo do SNR) quando
| f (t) = Kh(- t). |
(8-4.13) |
Este valor do filtro f (t)
mathend000# é chamado filtro adaptado ou matched filter. Mais, quando f (t)
mathend000# é o matched filter então obtemos o valor máximo do SNR que é
SNRmax = 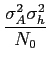 , , |
(8-4.14) |
onde
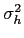 mathend000# é a energia na função de pulso recebida
mathend000# é a energia na função de pulso recebida
O matched filter tem como resposta impulsiva a forma do sinal de entrada revertida no tempo (time-reversed), h(- t)
mathend000# e a sua TF é
H * ( )
mathend000# isto é o conjugado da forma do sinal de entrada. Podemos assim perceber que a resposta do filtro adaptado igualiza (ou compensa) exactamente a fase do sinal de entrada resultando numa saída que é real e igual a
|H(
)
mathend000# isto é o conjugado da forma do sinal de entrada. Podemos assim perceber que a resposta do filtro adaptado igualiza (ou compensa) exactamente a fase do sinal de entrada resultando numa saída que é real e igual a
|H( )
)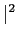 mathend000#. O valor do sinal de saída do filtro adaptado escreve-se a partir de (8-4.3) como
mathend000#. O valor do sinal de saída do filtro adaptado escreve-se a partir de (8-4.3) como
o que não é mais do que o valor da função de correlação entre a entrada e a forma de pulso esperada para o instante t = 0
mathend000#. Por isso filtro adaptado é por vezes também chamado receptor-correlador.
Demonstrámos que o filtro adaptado constitui o receptor óptimo de um único impulso em ruído branco e Gaussiano. Este resultado pode ser facilmente generalizado ao caso de uma sucessão de impulsos desde que não exista ISI. Para que tal aconteça é necessário e suficiente que cada impulso h(t)
mathend000# do sinal recebido esteja contido num e só num intervalo de símbolo.
O receptor óptimo em banda base
A transmissão de uma trama de bits requer, a escolha dos sinais representativos dos símbolos '0' e '1' - chama-se a isto o processo de sinalização. Vamos supôr que é feita a seguinte sinalização
| 0 |
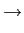 |
s0(t) |
|
| 1 |
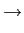 |
s1(t) |
|
no intervalo
0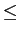 t
t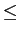 Tb
mathend000# onde Tb
mathend000# é o intervalo de amostragem da trama de bits, i.e.,
Tb = 1/fb
mathend000#, onde fb
mathend000# é a cadência de amostragem da trama de bits. A sequência temporal obtida é modulada, transmitida e na recepção deverá ser efectuada uma detecção, de cada sinal si(t)
mathend000# enviado e a ele associado um bit i
mathend000#. Vamos supôr que o canal de transmissão é de tipo aditivo e que o ruído pode ser representado por uma sequência aleatória estacionária, branca, Gaussiana e de média nula. Assim, o sinal recebido y(t)
mathend000# pode-se escrever
Tb
mathend000# onde Tb
mathend000# é o intervalo de amostragem da trama de bits, i.e.,
Tb = 1/fb
mathend000#, onde fb
mathend000# é a cadência de amostragem da trama de bits. A sequência temporal obtida é modulada, transmitida e na recepção deverá ser efectuada uma detecção, de cada sinal si(t)
mathend000# enviado e a ele associado um bit i
mathend000#. Vamos supôr que o canal de transmissão é de tipo aditivo e que o ruído pode ser representado por uma sequência aleatória estacionária, branca, Gaussiana e de média nula. Assim, o sinal recebido y(t)
mathend000# pode-se escrever
| y(t) = si(t) + n(t), |
(8-5.01) |
O problema no receptor consiste em, com o mínimo erro possível, e partindo de
{y(t), 0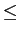 t
t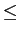 Tb}
mathend000# determinar se um bit '0' ou um bit '1' foi emitido.
Tb}
mathend000# determinar se um bit '0' ou um bit '1' foi emitido.
No caso do problema exposto acima, o receptor óptimo é o receptor-correlacionador ou 'matched-filter'. O receptor-correlacionador é constituido por dois blocos: um multiplicador e um integrador. O receptor-correlacionador (que no caso binário é constituido por dois correlacionadores) implementa a seguinte operação no sinal de entrada
ri(t) = 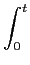 y( y( )si( )si( )d )d , 0 , 0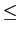 t t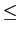 Tb Tb |
(8-5.02) |
Quando o sinal s0(t)
mathend000# é transmitido obtem-se
| r0(t) |
= |
A + n0 |
|
| r1(t) |
= |
A12 + n1, |
(8-5.03) |
e quando s1(t)
mathend000# é transmitido
| r0(t) |
= |
A12 + n0 |
|
| r1(t) |
= |
A + n1, |
(8-5.04) |
onde se supõe
A = 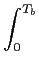 s02(t)dt = s02(t)dt = 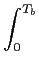 s12(t)dt e A12 = s12(t)dt e A12 = 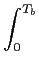 s1(t)s0(t)dt, s1(t)s0(t)dt, |
(8-5.05) |
e ainda que
ni = 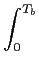 n(t)si(t)dt. n(t)si(t)dt. |
(8-5.06) |
Dado que n(t)
mathend000# é uma sequência aleatória, branca, Gaussiana de média nula e de variância 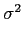 mathend000#, temos que ni
mathend000# será também branca e Gaussiana com média
mathend000#, temos que ni
mathend000# será também branca e Gaussiana com média
E[ni] = 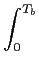 si(t)E[n(t)]dt = 0, si(t)E[n(t)]dt = 0, |
(8-5.07) |
e variância
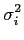 |
= |
E[ni2] |
|
| |
= |
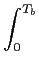 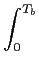 si(t)si( si(t)si( )E[n(t)n( )E[n(t)n( )]dtd )]dtd |
|
| |
= |
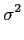 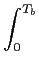 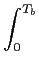 si(t)si( si(t)si( ) )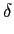 (t - (t -  )dtd )dtd |
|
| |
= |
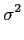 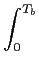 si2(t)dt si2(t)dt |
|
| |
= |
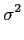 A, A, |
(8-5.08) |
e assim, temos que as densidades de probabilidade de r0
mathend000# e r1
mathend000# quando, por exemplo s0(t)
mathend000# é transmitido, se escrevem
| p(r0/s0) |
= |
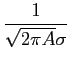 exp[- (r0 - A)2/2 exp[- (r0 - A)2/2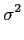 A] A] |
|
| p(r1/s0) |
= |
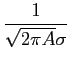 exp[- (r1 - A12)2/2 exp[- (r1 - A12)2/2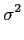 A], A], |
|
respectivamente, e que estão representadas na figura 8.7.
Figura 8.7:
densidades de probabilidade para r0
mathend000# e r1
mathend000# quando s0(t)
mathend000# é transmitido e com A12
mathend000#=0.25, A = 1
mathend000# e 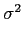 mathend000#=0.05.
mathend000#=0.05.
|
|
Obviamente no caso contrário, em que s1(t)
mathend000# é transmitido, temos que r0
mathend000# terá média A12
mathend000# e r1
mathend000# média A, sendo ambas as distribuições de variância
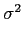 A
mathend000#.
A
mathend000#.
O filtro adaptado do sinal
{s(t), 0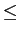 t
t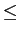 Tb}
mathend000# é um sistema cuja resposta impulsiva é s(Tb - t)
mathend000#. Assim, a resposta do filtro adaptado ao sinal s(t)
mathend000# é a convolução de s(t)
mathend000# com s(Tb - t)
mathend000#, i.e.,
Tb}
mathend000# é um sistema cuja resposta impulsiva é s(Tb - t)
mathend000#. Assim, a resposta do filtro adaptado ao sinal s(t)
mathend000# é a convolução de s(t)
mathend000# com s(Tb - t)
mathend000#, i.e.,
| x(t) |
= |
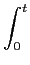 s( s( )h(t - )h(t -  )d )d |
|
| |
= |
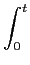 s( s( )s(Tb - t + )s(Tb - t +  )d )d . . |
(8-5.09) |
Se a saída de x(t)
mathend000# for amostrada no instante Tb
mathend000#, temos que
x(Tb) = 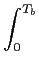 s2( s2( )d )d = A, = A, |
(8-5.10) |
podendo-se concluir que a saída do filtro adaptado amostrado à cadência da trama de bits é igual à saída do receptor-correlacionador.
O detector é um dispositivo que observa a saída do receptor-correlacionador ou filtro adaptado e decide qual dos dois símbolos, '0' ou '1', foi transmitido. Pretende-se, obviamente, que este processo de decisão tenha o menor erro possível. A probabilidade de erro, Pe
mathend000#, quando p.ex. s0
mathend000# é transmitido, escreve-se como sendo a probabilidade de decidir que s1(t)
mathend000# foi recebido quando na realidade foi s0(t)
mathend000#, assim podemos dizer que
| Pe = Prob(r1 > r0) = Prob(n1 + A12 > A + n0) = Prob(n1 - n0 > A - A12), |
(8-5.11) |
e como n1
mathend000# e n0
mathend000# são variáveis aleatórias Gaussianas, de média nula, a sua diferença,
x = n1 - n0
mathend000# também é Gaussiana de média nula. A variância de x
mathend000# pode-se calcular através de
| E[x2] = E[(n1 - n0)2] = E[n12] + E[n22] - 2E[n1n0], |
(8-5.12) |
onde
E[ni2] = A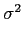 mathend000# e
mathend000# e
| E[n1n0] |
= |
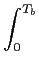 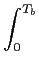 s0(t)s1( s0(t)s1( )E[n(t)n( )E[n(t)n( )]dtd )]dtd |
|
| |
= |
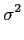 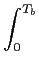 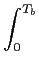 s0(t)s1( s0(t)s1( ) )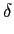 (t - (t -  )dtd )dtd |
|
| |
= |
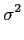 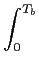 s0(t)s1(t)dt s0(t)s1(t)dt |
|
| |
= |
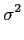 A12. A12. |
(8-5.13) |
Finalmente
E[x2] = 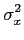 = 2 = 2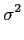 (A - A12), (A - A12), |
(8-5.14) |
de onde, utilizando (8-5.11), podemos escrever a probabilidade de erro como
| Pe = Prob(x > A - A12) |
(8-5.15) |
onde X = n1 - n0
mathend000#. Dado que n1
mathend000# e n0
mathend000# são distribuídos de acordo com uma lei Normal de média nula e de mesma variância 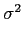 mathend000#, então X
mathend000#
também vai seguir uma lei Normal de média nula e de variância
mathend000#, então X
mathend000#
também vai seguir uma lei Normal de média nula e de variância
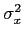 = 2
= 2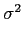 mathend000#. Assim podemos escrever
mathend000#. Assim podemos escrever
fazendo a mudança de variável
u = x/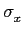 mathend000# obtemos
mathend000# obtemos
Pe = 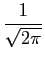 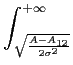 e-u2/2du = Q e-u2/2du = Q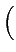 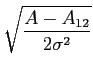 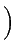 . . |
(8-5.17) |
onde Q( . )
mathend000# é a função ``cauda de Gauss'', normalmente chamada Q function (Matlab qfunc) e que é definida por
Q(x) = 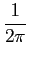 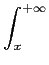 e-x2/2dx e-x2/2dx |
(8-5.18) |
Para os valores de A12
mathend000#, A
mathend000# e 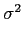 mathend000# da figura 8.7 a probabilidade de erro toma o valor
Pe = 0.0013
mathend000#. É comum representar-se o desempenho de um sistema de comunicação como a taxa de erro por bit (BER bit error rate) em função da relação sinal ruído por bit (signal to noise ratio per bit - SNRB). A SNRB é normalmente definida como sendo a energia contida num bit (
mathend000# da figura 8.7 a probabilidade de erro toma o valor
Pe = 0.0013
mathend000#. É comum representar-se o desempenho de um sistema de comunicação como a taxa de erro por bit (BER bit error rate) em função da relação sinal ruído por bit (signal to noise ratio per bit - SNRB). A SNRB é normalmente definida como sendo a energia contida num bit (
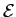 b
mathend000#) dividida pela energia do ruído. Assim para o caso ASK (ou PAM)
b
mathend000#) dividida pela energia do ruído. Assim para o caso ASK (ou PAM)
SNRB = 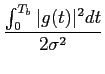 |
(8-5.19) |
onde o factor 2 é devido à relação (2-2.62). A figura 8.8 representa a BER (em dB) em função da SNRB para o caso binário com sinais não ortogonais nem antipodais.
Figura 8.8:
taxa de erro de bit (BER) em função da relação sinal ruído por bit (SNRB) em dB para o caso binário (M
mathend000#=2), sinais não ortogonais nem antipodais e nas condições da figura 8.7.
|
|
No processo de sinalização vários conjuntos de sinais podem ser utilizados e as características dos receptor-correlacionador/matched-filter serão em cada caso diferentes. Dois sinais s0(t)
mathend000# e s1(t)
mathend000# são ditos ortogonais no intervalo [0, T]
mathend000# se
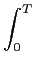 s0(t)s1(t)dt = 0. s0(t)s1(t)dt = 0. |
|
Dois sinais são ditos antipodais se
s0(t) = - s1(t), 0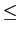 t t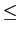 T. T. |
|
O tipo de codificação on-off é tal que, p.ex., sejam associados os seguintes sinais
| 0 |
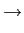 |
sem sinal |
|
| 1 |
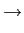 |
s(t), |
|
o que significa que o sinal recebido é do tipo
y(t) = 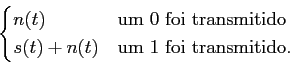 |
(8-5.20) |
Se um sistema de transmissão utilizar sinais ortogonais temos que
A12 = 0
mathend000# o que implica que as médias das densidades de probabilidade
p(r1/s0)
mathend000# e
p(r0/s1)
mathend000# são ambas nulas. No caso dos sinais antipodais temos que essas mesmas densidades são de média - A
mathend000# e por isso a diferença média entre as duas densidades é aumentada. As funções de erro são modificadas da mesma forma.
Se em vez disso utilizarmos uma sinalização on-off, temos que as distribuições são semelhantes às do caso dos sinais ortogonais, a probabilidade de erro é portanto mais elevada do que no caso antipodal mas temos a considerar que existe um ganho de 2 na potência a transmitir, visto que só é transmitido um sinal em cada 2 bits, em média se um bit '0' tiver a mesma probabilidade que um bit '1'.
A técnica mais utilizada em transmissão de informação através de modulação de impulsos (PM), é chamada sinalização multinível e tem como particularidade utilizar uma única forma de impulso que toma um nível diferente (dentro de um número de níveis finito possíveis) para cada símbolo a transmitir. No caso geral temos um sinal do tipo
sm(t) = Amg(t), 0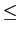 t t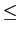 Ts, m = 0, 1,..., M - 1 Ts, m = 0, 1,..., M - 1 |
(8-5.21) |
onde as amplitudes Am
mathend000# são dadas por
| Am = (2m - M + 1)d, m = 0, 1,..., M - 1 |
|
g(t)
mathend000# é um impulso rectangular e o número de níveis M
mathend000# é dado por M = 2k
mathend000#, k
mathend000# inteiro. O período Ts
mathend000# é geralmente chamado taxa de símbolo (ou symbol rate) enquanto a taxa de bit (ou bit rate) Tb
mathend000# é dada por Tb = T/k
mathend000#, i.e., a sinalização multiníveis permite enviar k
mathend000# vezes mais informação do que um método de sinalização binário. O que nos interessa aqui porém, é a forma do sistema detector óptimo, se ele existe. Na verdade existe, pelo menos para o caso de ruído branco e Gaussiano, e é dado pelo receptor-correlacionador tal como no caso do nível simples. É fácil de provar que a saída do receptor-correlacionador para o sinal de nível si(t)
mathend000#
é
| r(t) = Ai + n(t), |
(8-5.22) |
enquanto a densidade de probabilidade se escreve
p(r|si(t)) = 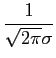 exp - [(r - Ai)2/2 exp - [(r - Ai)2/2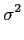 ], ], |
(8-5.23) |
onde Ai
mathend000# é um dos valores de entre os M
mathend000# possíveis. Prova-se neste caso que a probabilidade de erro do detector óptimo de M
mathend000# níveis se escreve
onde Aavg
mathend000# é a energia média de um bit de informação. A curva da BER em função da SNRB encontra-se na figura 8.9.
Figura 8.9:
taxa de erro de bit (BER) em função da relação sinal ruído por bit (SNRB) em dB para ASK e vários valores de M
mathend000#.
|
|
Resumo do capítulo 8:
O receptor é abordado do ponto de vista do seu carácter óptimo, começando pelo desmodulador , depois pela representação em banda base. A derivação formal do receptor óptimo a partir da maximização da probabilidade à posteriori (MAP) de obter um determinado sinal em ruído Gaussiano aditivo, sabendo que ele foi emitido, leva directamente ao receptor - correlacionador. Desmonstra-se ainda que o resultado é idêntico aquele obtido pelo critério de máxima verosimílhança (ML) - no caso Gaussiano. Por último demonstra-se que o mesmo resultado pode ser obtido / implementado por um filtro adaptado que ele é indenpendente da distribuição do ruído. Finalmente estabelece-se um caso de aplicação simples (depois revisto em TP) a partir da sinalização - ortogonal, antipodal e on-off - o receptor óptimo, densidade de probabilidade de detecção e de erro para cada caso.
Sergio Jesus
2008-12-30
![\includegraphics[width=13cm]{figs/fig6-7.eps}](img481.png)
![\includegraphics[width=10cm]{figs/fig6-8.eps}](img482.png)
![]() ) = N0/2
) = N0/2
![\includegraphics[width=11cm]{figs/fig6-9.eps}](img484.png)
![]() ) = G(
) = G(![]() )B(
)B(![]() +
+ ![]() )F(
)F(![]() ),
),![]() +
+ ![]() )
)
![]() )
)
![]()
![]() )
)
![]() )
)
![]() +
+ ![]() )G(
)G(![]() )
)
![]() )
)
![]() )
)
![]() )G(
)G(![]() ) = 0
) = 0
![]() )
)
![]() )
)
![]()
![]() ] = 1
] = 1
![]() )
)
![]() )
)
![]() )
)
![]()
![]() )G(
)G(![]() )
)
![]() )
)
![]()
![]() =
= ![]() +
+ ![]()
![]() |
|![]() ]
]
![]()
![]()
![]()
![]() |
|![]() ]
]
![]()
![]()
![]() ]
]
![]() ]
]
![]() ] = 1/M;m = 1,..., M
] = 1/M;m = 1,..., M
![]()
![]() |
|![]() ]
]
![]() ]
]
![]()
![]() |
|![]() ]
]
![]()
![]() = 2
= 2![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]() )
)
![]() ,
,![]() )
)
![]() .
. ![]() ;m = 1,..., M}
;m = 1,..., M}
![]()
![]()
![]()
![]() ;m = 1,..., M}
;m = 1,..., M}
![]()
![]()
![]() ,
,![]() ) = 2
) = 2![]() r(t)sm(t)dt -
r(t)sm(t)dt - ![]() m m = 1,..., M
m m = 1,..., M![]() = 0
= 0
![]() ,
,![]() )
)
![]() = 0
= 0
![]() Pn(f )
Pn(f )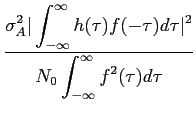
![]()
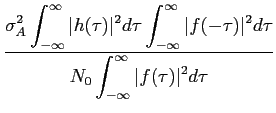
![]()
![]() )
)
![]() )
)![]()
![]()
![]()
![]() t
t![]() Tb
Tb
![]() t
t![]() Tb}
Tb}
![]() y(
y(![]() )si(
)si(![]() )d
)d![]() , 0
, 0![]() t
t![]() Tb
Tb![]() s02(t)dt =
s02(t)dt = ![]() s12(t)dt e A12 =
s12(t)dt e A12 = ![]() s1(t)s0(t)dt,
s1(t)s0(t)dt,![]() n(t)si(t)dt.
n(t)si(t)dt.![]()
![]() si(t)E[n(t)]dt = 0,
si(t)E[n(t)]dt = 0,![]()
![]()
![]() si(t)si(
si(t)si(![]() )E[n(t)n(
)E[n(t)n(![]() )]dtd
)]dtd![]()
![]()
![]()
![]() si(t)si(
si(t)si(![]() )
)![]() (t -
(t - ![]() )dtd
)dtd![]()
![]()
![]() si2(t)dt
si2(t)dt![]() A,
A,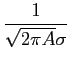 exp[- (r0 - A)2/2
exp[- (r0 - A)2/2![]() A]
A]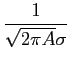 exp[- (r1 - A12)2/2
exp[- (r1 - A12)2/2![]() A],
A],![]()
![\includegraphics[width=8cm]{figs/fig8_7.eps}](img528.png)
![]() A
A
![]() t
t![]() Tb}
Tb}
![]() s2(
s2(![]() )d
)d![]() = A,
= A,![]()
![]()
![]() s0(t)s1(
s0(t)s1(![]() )E[n(t)n(
)E[n(t)n(![]() )]dtd
)]dtd![]()
![]()
![]()
![]() s0(t)s1(
s0(t)s1(![]() )
)![]() (t -
(t - ![]() )dtd
)dtd![]()
![]()
![]() s0(t)s1(t)dt
s0(t)s1(t)dt![]() A12.
A12.![]() = 2
= 2![]() (A - A12),
(A - A12),![]()
![]() = 2
= 2![]()
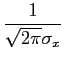
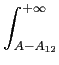 e-x2/2
e-x2/2![]() dx,
dx,![]()
![]()
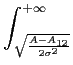 e-u2/2du = Q
e-u2/2du = Q![]()
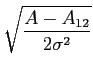
![]() .
.![]()
![]() b
b
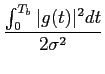
![\includegraphics[width=8cm]{figs/fig8_8.eps}](img542.png)
![]() s0(t)s1(t)dt = 0.
s0(t)s1(t)dt = 0.![]() t
t![]() T.
T.![]()
![]()
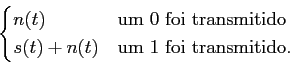
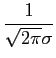 exp - [(r - Ai)2/2
exp - [(r - Ai)2/2![]() ],
],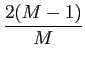 Q
Q![]()
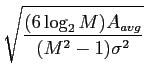
![]() ,
,![\includegraphics[width=8cm]{figs/fig8_9.eps}](img549.png)

![\includegraphics[width=13cm]{figs/fig6-10.eps}](img486.png)

![$\displaystyle {{E[\vert A_k \vert^2]}\over {\sigma_u^2}}$](img489.png) .
.![\includegraphics[width=13cm]{figs/fig6-5.eps}](img491.png)
![$\displaystyle {{P[{\bf r} \vert {\bf s}_m] P[{\bf s}_m]}\over {P[{\bf r}]}}$](img495.png) ,
,![$\displaystyle {{P[{\bf r} \vert {\bf s}_m]}\over {P[{\bf r}]}}$](img497.png) ,
,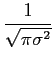 exp
exp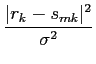
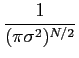 exp
exp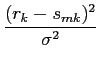
![\includegraphics[width=12cm]{figs/correl-receiver.eps}](img510.png)
 ,
,