



Next: Circuitos RC e RLC
Up: Corrente alternada
Previous: Regime permanente sinusoidal
Contents
O facto já mencionado anteriormente de que uma excitação sinusoidal a uma determinada pulsação 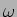 , tem como reposta em regime permanente ainda uma forma sinusoidal de mesma pulsação, e apenas com uma diferença de fase e de amplitude, motivou a introdução de uma noção simplificativa que é a noção de fasor.
, tem como reposta em regime permanente ainda uma forma sinusoidal de mesma pulsação, e apenas com uma diferença de fase e de amplitude, motivou a introdução de uma noção simplificativa que é a noção de fasor.
Comecemos por considerar a família de excitações exponenciais complexas:
![\begin{displaymath}
x(t) = \cases{\Re[\vec X] = \Re [\vert \vec X \vert
e^{j\theta} e^{(\alpha+j\omega)t}]& t $>$ 0;\cr 0 & t $<$ 0,\cr}
\end{displaymath}](img775.png) |
(6-3.01) |
onde 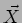 é um vector, possivelmente complexo, e onde
é um vector, possivelmente complexo, e onde ![$\Re [\cdot]$](img777.png) é o operador ``parte real de''. Podemos ainda notar a equação (6-3.1) como
é o operador ``parte real de''. Podemos ainda notar a equação (6-3.1) como
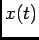 |
 |
![$\displaystyle \Re[\vec X]$](img779.png) |
(6-3.02) |
| |
 |
![$\displaystyle \Re[\vert X \vert e^{\alpha t} e^{j(\omega t + \theta)}]$](img780.png) |
(6-3.03) |
| |
 |
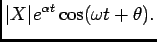 |
(6-3.04) |
Este vector encontra-se representado na figura 6.3, onde podemos notar que 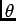 é o ângulo inicial que o vector faz com o eixo das abcissas, ou termo de fase do sinal no domínio do tempo,
é o ângulo inicial que o vector faz com o eixo das abcissas, ou termo de fase do sinal no domínio do tempo, 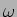 representa a velocidade com a qual o vector gira em torno à origem quanto o tempo aumenta e
representa a velocidade com a qual o vector gira em torno à origem quanto o tempo aumenta e 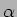 é um coeficiente de atenuação de amplitude. Trata-se portanto de uma família de funções que, segundo os valores de relativos de
é um coeficiente de atenuação de amplitude. Trata-se portanto de uma família de funções que, segundo os valores de relativos de 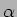 ,
, 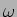 e
e 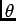 pode tomar as formas de exponencial pura (quando
pode tomar as formas de exponencial pura (quando  ), sinusoidal pura (quando
), sinusoidal pura (quando  ) ou ainda sinusoidal amortecida,
) ou ainda sinusoidal amortecida, 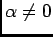 e
e 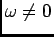 .
.
Figura 6.3:
representação do fasor.
|
|
A regime permanente sinusoidal obtem-se para  e nesse caso
e nesse caso
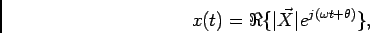 |
(6-3.05) |
cuja interpretação é a de um vector 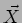 rodando no plano complexo no sentido anti-horário com uma pulsação
rodando no plano complexo no sentido anti-horário com uma pulsação 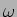 como representado na figura 6.3. Este vector é chamado fasor ou vector de Fresnel. Se considerarmos a projeção deste vector no eixo real temos
como representado na figura 6.3. Este vector é chamado fasor ou vector de Fresnel. Se considerarmos a projeção deste vector no eixo real temos
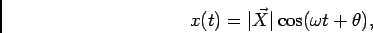 |
(6-3.06) |
que não é mais do que uma função sinusoidal de amplitude
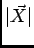 e pulsação
e pulsação 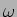 como temos vindo a considerar ao longo deste capítulo. A hipótese simplificadora reside em considerar não o sinal real
como temos vindo a considerar ao longo deste capítulo. A hipótese simplificadora reside em considerar não o sinal real 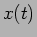 mais sim a sua representação complexa
mais sim a sua representação complexa 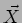 e realizar todo o cálculo em álgebra complexa sabendo de antemão que o resultado será a parte real de
e realizar todo o cálculo em álgebra complexa sabendo de antemão que o resultado será a parte real de
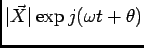 .
.
A título de exemplo, vamos refazer o cálculo efectuado para o circuito RL série do capítulo 6.2 usando agora a notação complexa. Observando a figura 6.1 podemos escrever o fasor 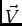 associado com a tensão
associado com a tensão 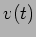 como
como
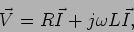 |
(6-3.07) |
onde 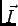 é o fasor associado com a corrente
é o fasor associado com a corrente 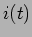 e a queda de tensão aos terminais da bobine
e a queda de tensão aos terminais da bobine
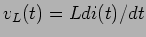 é simplesmente substituida por
é simplesmente substituida por
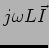 visto que
visto que
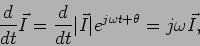 |
(6-3.08) |
e aqui reside toda a simplificação da notação complexa: as derivadas tornam-se multiplicações por 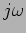 e os integrais tornam-se divisões por
e os integrais tornam-se divisões por 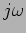 e, como resultado, as equações diferenciais tornam-se equações algébricas em
e, como resultado, as equações diferenciais tornam-se equações algébricas em 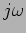 !
!
Voltando a (6-3.7) escrevemos
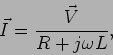 |
(6-3.09) |
e a solução final encontra-se tomando a parte real de cada lado de (6-3.9) de onde se obtem
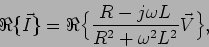 |
(6-3.10) |
de onde substituindo 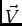 por
por
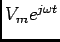 obtemos
obtemos
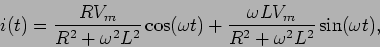 |
(6-3.11) |
e que é o resultado esperado se substituirmos (6-2.6) e (6-2.7) em (6-2.2).
Como antevisto em (6-3.8), em regime permanente sinusoidal e usando a notação complexa, a bobine tem uma queda de tensão
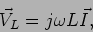 |
(6-3.12) |
que é a forma da lei de Ohm em notação complexa e que introduz a noção de impedância  tal que
tal que
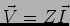 e no exemplo acima a impedância da bobine é
e no exemplo acima a impedância da bobine é 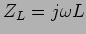 .
.
Fazendo o mesmo raciocínio com o condensador temos que,
 |
(6-3.13) |
permite-nos achar a representação em termos de fasores respectiva,
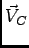 |
 |
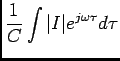 |
(6-3.14) |
| |
 |
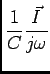 |
(6-3.15) |
| |
 |
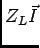 |
(6-3.16) |
com a impedância equivalente
Será fácil verificar que no caso de uma resistência 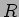 , a tensão e corrente sob forma de
fasor se encontram ligados por uma impedância
, a tensão e corrente sob forma de
fasor se encontram ligados por uma impedância 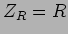 .
.




Next: Circuitos RC e RLC
Up: Corrente alternada
Previous: Regime permanente sinusoidal
Contents
Sergio Jesus
2003-12-07
![]() , tem como reposta em regime permanente ainda uma forma sinusoidal de mesma pulsação, e apenas com uma diferença de fase e de amplitude, motivou a introdução de uma noção simplificativa que é a noção de fasor.
, tem como reposta em regime permanente ainda uma forma sinusoidal de mesma pulsação, e apenas com uma diferença de fase e de amplitude, motivou a introdução de uma noção simplificativa que é a noção de fasor.
![]() e nesse caso
e nesse caso
![]() associado com a tensão
associado com a tensão ![]() como
como
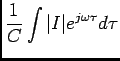
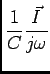
![]() , a tensão e corrente sob forma de
fasor se encontram ligados por uma impedância
, a tensão e corrente sob forma de
fasor se encontram ligados por uma impedância ![]() .
.