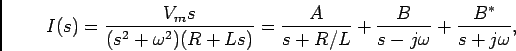Next: Notação complexa e impedâncias
Up: Corrente alternada
Previous: Introdução
Contents
Nos capítulos anteriores estudámos a resposta transitória de alguns circuitos com condensadores, bobines e resistências. Vimos que essa resposta transitória correspondia, em termos das soluções das equações diferenciais dos circuitos, à solução sem excitação. Esta solução também é chamada resposta natural ou não forçada. A introdução do sinal de excitação no segundo membro dava origem a uma solução particular e ao regime permanente quando 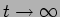 .
.
Vamos agora estudar a resposta forçada sem nos interessarmos do regime transitório quando o sinal de excitação é uma onda sinusoidal. A resposta forçada dá, neste caso, origem ao regime permanente sinusoidal.
Como exemplo vamos considerar o circuito RL série da figura 6.1 quando
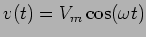 .
.
Figura 6.1:
circuito RL série em regime sinusoidal.
|
|
Neste caso, depois de passado o regime transitório, no qual intervem a indução inicial na bobine, o circuito deverá obedecer à seguinte equação
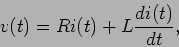 |
(6-2.01) |
sabendo à partida que a solução da equação terá também uma forma sinusoidal podemos procurar soluções do tipo
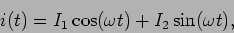 |
(6-2.02) |
derivando e substituindo em (6-2.1) obtemos
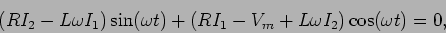 |
(6-2.03) |
que só se verifica se
visto que uma função seno e coseno de mesma pulsação nunca se anulam simultâneamente. Resolvendo em relação a 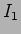 e
e 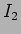 permite obter
permite obter
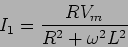 |
(6-2.06) |
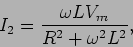 |
(6-2.07) |
de onde podemos substituir em (6-2.2) e fazendo
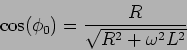 |
(6-2.08) |
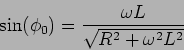 |
(6-2.09) |
escrever a forma final para a corrente
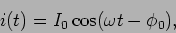 |
(6-2.10) |
com a amplitude
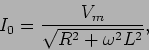 |
(6-2.11) |
e o termo de fase
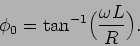 |
(6-2.12) |
Figura 6.2:
 ,
, 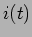 e
e 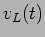 no circuito da figura
6.1.
no circuito da figura
6.1.
|
|
Poderíamos ainda deduzir a tensão 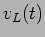 aos terminais da bobine que seria neste caso
aos terminais da bobine que seria neste caso
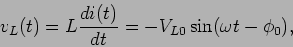 |
(6-2.13) |
onde
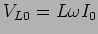 . Usando a relação
. Usando a relação
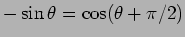 podemos notar que,
podemos notar que,
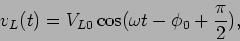 |
(6-2.14) |
o que nos permite determinar que 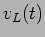 se encontra adiantado de
se encontra adiantado de 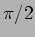 em relação à corrente
em relação à corrente 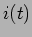 . A figura 6.2 representa a tensão
. A figura 6.2 representa a tensão 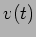 , a corrente
, a corrente 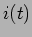 e a tensão
e a tensão 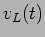 para
para 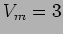 v,
v, 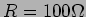 ,
,  H e
H e 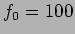 Hz.
Hz.
De uma forma alternativa poderíamos empregar a TL para resolver este circuito utilizando directamente as ferramentas do cálculo simbólico. Assim podemos escrever directamente
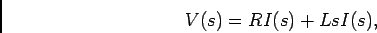 |
(6-2.15) |
e por isso
 |
(6-2.16) |
com
![$V(s)={\rm TL}[v(t)]=V_m s/(s^2+\omega^2)$](img769.png) . Substituindo em (6-2.16) e decompondo a fração em
. Substituindo em (6-2.16) e decompondo a fração em 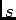 ,
,
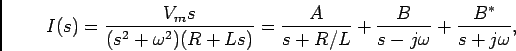 |
(6-2.17) |
com
Podemos então deduzir a corrente 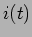
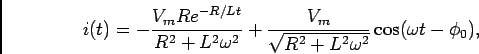 |
(6-2.18) |
onde
 . A análise da expressão (6-2.18) mostra-nos que a solução do problema é formada por dois termos: o primeiro diz respeito ao regime transitório com a constante de tempo
. A análise da expressão (6-2.18) mostra-nos que a solução do problema é formada por dois termos: o primeiro diz respeito ao regime transitório com a constante de tempo 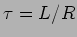 , como encontrado nos exemplos do capitulo 5, e o segundo diz respeito ao regime permanente sinusoidal e é idêntico à solução (6-2.10) com (6-2.11) e (6-2.12).
, como encontrado nos exemplos do capitulo 5, e o segundo diz respeito ao regime permanente sinusoidal e é idêntico à solução (6-2.10) com (6-2.11) e (6-2.12).




Next: Notação complexa e impedâncias
Up: Corrente alternada
Previous: Introdução
Contents
Sergio Jesus
2003-12-07
![]() .
.
![]() .
.
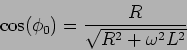
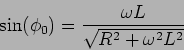
![]() aos terminais da bobine que seria neste caso
aos terminais da bobine que seria neste caso