



Next: Corrente alternada
Up: Circuitos em regime transitório
Previous: Circuitos de segunda ordem
Contents
Exemplo 1: Considere o circuito da figura 5.10 (R'=10 K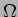 , R=1 K
, R=1 K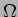 , C=10
, C=10 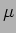 F, E=10 V).
F, E=10 V).
Figura 5.10:
circuito do Exemplo 1.
|
|
a) calcule a expressão literal de 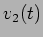 em função de
em função de 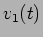 .
.
b) se o sinal 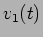 tiver a forma representada na figura 5.11
tiver a forma representada na figura 5.11
Figura 5.11:
tensão 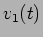 no circuito da figura 5.10.
no circuito da figura 5.10.
|
|
Determinar a forma de 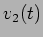 para T=2 s, T=20 ms e T=2 ms.
para T=2 s, T=20 ms e T=2 ms.
a) notando a corrente que percorre 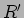 ,
, 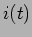 e as correntes em
e as correntes em 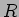 e
e 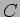 respectivamente
respectivamente 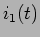 e
e 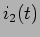 podemos escrever
podemos escrever
mas
substituindo (c) em (a),
ou ainda
b) vamos optar por definir dois intervalos temporais: um para
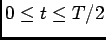 e outro para
e outro para
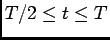 . Calculando agora a TL da equação do circuito e utilizando o dado que
. Calculando agora a TL da equação do circuito e utilizando o dado que 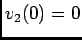 no primeiro intervalo,
no primeiro intervalo,
ou ainda
que depois de algum arranjo e com 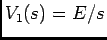 (visto que estamos no intervalo
(visto que estamos no intervalo 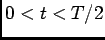 )
)
com
Como habitualmente a TLI permite obter a forma temporal da tensão 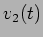 procurada
procurada
com os valores númericos  ms e
ms e
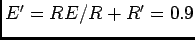 v. Portanto a forma de
v. Portanto a forma de 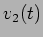 é uma exponencial de carga do condensador com a constante de tempo de 9ms. Para T=2 s temos que T/2
é uma exponencial de carga do condensador com a constante de tempo de 9ms. Para T=2 s temos que T/2 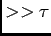 e
e
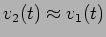 , para T=20 ms a constante de tempo é da ordem de grandeza de T/2 e por isso temos uma exponencial perfeita até 0.9 v. No caso extremo em que T=2ms, T/2
, para T=20 ms a constante de tempo é da ordem de grandeza de T/2 e por isso temos uma exponencial perfeita até 0.9 v. No caso extremo em que T=2ms, T/2 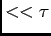 e nesse caso vê-se apenas o início da exponencial o que parece uma linha recta oblíqua - que pode ser confundido com uma onda triangular. Neste último caso dizemos que o sinal de saída
e nesse caso vê-se apenas o início da exponencial o que parece uma linha recta oblíqua - que pode ser confundido com uma onda triangular. Neste último caso dizemos que o sinal de saída 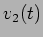 é aproximadamente o integral do sinal de entrada
é aproximadamente o integral do sinal de entrada 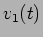 .
.
No segundo intervalo de tempo, i.e., quanto
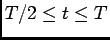 , a tensão de entrada
, a tensão de entrada 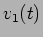 muda de
muda de 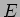 para
para 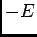 volts, o circuito comporta-se de forma idêntica ao exemplo do circuito RC estudado no início deste capítulo, com a diferença que em vez de uma tensão
volts, o circuito comporta-se de forma idêntica ao exemplo do circuito RC estudado no início deste capítulo, com a diferença que em vez de uma tensão 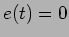 volts temos uma tensão negativa de
volts temos uma tensão negativa de 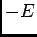 volts, de onde podemos desde já prever que o condensador em vez de se descarregar nas resistências
volts, de onde podemos desde já prever que o condensador em vez de se descarregar nas resistências 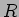 e
e 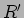 , se vai carregar a uma tensão de polaridade contrária de valor
, se vai carregar a uma tensão de polaridade contrária de valor
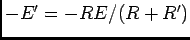 . Mas, vamos ver as equações. Admitindo que no instante
. Mas, vamos ver as equações. Admitindo que no instante 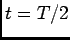 a tensão atingida era
a tensão atingida era
![$v_2(T/2)=E'[1-\exp{(-T/2\tau)}]$](img716.png) , a TL da equação que rege o circuito escreve-se
, a TL da equação que rege o circuito escreve-se
ou seja
ou ainda, depois de mais alguma arrumação, e considerando que o novo sinal à entrada é 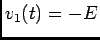 dando
dando
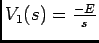 onde
onde 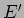 e
e 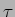 têm os valores habituais
têm os valores habituais
A decomposição em factores escreve-se agora
onde por identificação 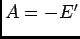 e
e
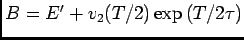 de onde tiramos directamente a TLI de
de onde tiramos directamente a TLI de 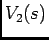
Esta equação permite traçar a resposta final do circuito para os dois intervalos para 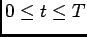 .
.
Exemplo 2: para o circuito RL da figura 5.12 determine:
- a)
- a potência total fornecida pela fonte
- b)
- a potência dissipada na resistência
- c)
- a potência armazenada na bobine
Figura 5.12:
circuito do Exemplo 2.
|
|
a) a potência fornecida pela fonte é
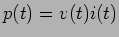 . Assim, podemos escrever
. Assim, podemos escrever
cuja TL com 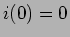 é
é
ou, em função de 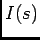 ,
,
Com 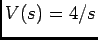 permite escrever
permite escrever
onde determinar a TLI de 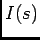 se faz como habitualmente decompondo em factores e
se faz como habitualmente decompondo em factores e
onde 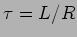 .
.
Finalmente a potência escreve-se
b) a potência dissipada na resistência é igualmente
c) a potência armazenada na bobine
ou seja




Next: Corrente alternada
Up: Circuitos em regime transitório
Previous: Circuitos de segunda ordem
Contents
Sergio Jesus
2003-12-07
![]() , R=1 K
, R=1 K![]() , C=10
, C=10 ![]() F, E=10 V).
F, E=10 V).
![]() em função de
em função de ![]() .
.
![]() tiver a forma representada na figura 5.11
tiver a forma representada na figura 5.11
![]() para T=2 s, T=20 ms e T=2 ms.
para T=2 s, T=20 ms e T=2 ms.
![]() ,
, ![]() e as correntes em
e as correntes em ![]() e
e ![]() respectivamente
respectivamente ![]() e
e ![]() podemos escrever
podemos escrever
![]() e outro para
e outro para
![]() . Calculando agora a TL da equação do circuito e utilizando o dado que
. Calculando agora a TL da equação do circuito e utilizando o dado que ![]() no primeiro intervalo,
no primeiro intervalo,
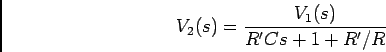

![]() , a tensão de entrada
, a tensão de entrada ![]() muda de
muda de ![]() para
para ![]() volts, o circuito comporta-se de forma idêntica ao exemplo do circuito RC estudado no início deste capítulo, com a diferença que em vez de uma tensão
volts, o circuito comporta-se de forma idêntica ao exemplo do circuito RC estudado no início deste capítulo, com a diferença que em vez de uma tensão ![]() volts temos uma tensão negativa de
volts temos uma tensão negativa de ![]() volts, de onde podemos desde já prever que o condensador em vez de se descarregar nas resistências
volts, de onde podemos desde já prever que o condensador em vez de se descarregar nas resistências ![]() e
e ![]() , se vai carregar a uma tensão de polaridade contrária de valor
, se vai carregar a uma tensão de polaridade contrária de valor
![]() . Mas, vamos ver as equações. Admitindo que no instante
. Mas, vamos ver as equações. Admitindo que no instante ![]() a tensão atingida era
a tensão atingida era
![]() , a TL da equação que rege o circuito escreve-se
, a TL da equação que rege o circuito escreve-se
![\begin{displaymath}V_2(s) = {{-E'/\tau - s v_2(T/2)[1-e^{-sT/2}]}\over {s(1/\tau + s)}}.\end{displaymath}](img721.png)
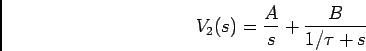
![]() . Assim, podemos escrever
. Assim, podemos escrever

