mathend000#.
Na prática, muito raramente poderemos calcular a DEP usando (2-3.10), pois esta necessita o conhecimento prévio de
rxx( )
mathend000# que é a função de autocorrelação dada por
)
mathend000# que é a função de autocorrelação dada por
rxx( ) = E[x(t + ) = E[x(t +  )x * (t)]. )x * (t)]. |
(B.-2.01) |
O cálculo do valor esperado necessitaria, em princípio, um número infinito de realizações do processo x(t)
mathend000#, o que na prática é irrealizável. Em vez disso, tenta-se substituir a média estatística de conjunto, por uma média temporal mediante a hipótese de ergodicidade. Para poder substituir a autocorrelação por uma função calculada a partir da média temporal, será necessário também que o sinal seja estacionário até ao quarto momento. Assim um primeiro estimador óbvio para a autocorrelação num intervalo finito T
mathend000# pode ser
 ( ( ) = ) = 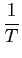  x(t + x(t +  )x * (t)dt, 0 )x * (t)dt, 0   Tm, com Tm Tm, com Tm T. T. |
(B.-2.02) |
Devido às propriedades de paridade da função de correlação, a expressão (B-2.2) pode ser estendida para valores
- T

 0
mathend000#, fazendo
r(1)xx(-
0
mathend000#, fazendo
r(1)xx(-  ) = r(1)xx(
) = r(1)xx( )
mathend000#, e portanto o estimador é forçosamente uma função limitada no intervalo [- T, T]
mathend000#, quando T
mathend000# é o intervalo de observação do sinal x(t)
mathend000#. No intuito de calcular o viés deste estimador, prova-se facilmente que
)
mathend000#, e portanto o estimador é forçosamente uma função limitada no intervalo [- T, T]
mathend000#, quando T
mathend000# é o intervalo de observação do sinal x(t)
mathend000#. No intuito de calcular o viés deste estimador, prova-se facilmente que
E[ ( ( )] )] |
= |
![$\displaystyle {{1\over T} \int_0^{T-\tau} E[x(t+\tau)x^{\ast}(t)]}$](img606.png) dt, 0 dt, 0   T T |
|
| |
= |
 , 0 , 0   T T |
|
| |
= |
rxx( )q2T( )q2T( ), 0 ), 0   T T |
(B.-2.03) |
onde
q2T( )
mathend000# é a função triangular
)
mathend000# é a função triangular
de amplitude unitária, abrangendo o intervalo [- T, T]
mathend000# e resultante da correlação entre as funções de observação rectangulares [0, T]
mathend000# do sinal x(t)
mathend000#. Podemos portanto dizer que
 (
( )
mathend000# é um estimador enviesado de
rxx(
)
mathend000# é um estimador enviesado de
rxx( )
mathend000#. No entanto, torna-se fácil ver que se trata de um estimador assimptoticamente não enviesado (consistente) em relação à média já que
)
mathend000#. No entanto, torna-se fácil ver que se trata de um estimador assimptoticamente não enviesado (consistente) em relação à média já que
 E[ E[ ( ( )] )] |
= |
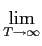  1 - 1 -   rxx( rxx( ) ) |
|
| |
= |
rxx( ). ). |
|
Prova-se ainda que para muitos sinais utilizados na prática este estimador apresenta um erro médio quadrático (mean square error ou MSE) inferior a um segundo estimador não enviesado e também muito utilizado que é
 ( ( ) = ) =   x(t + x(t +  )x * (t)dt, 0 )x * (t)dt, 0   Tm, com Tm Tm, com Tm T T |
(B.-2.05) |
da mesma forma que em (B-2.3) pode-se provar que a esperança matemática deste estimador se escreve
E[ ( ( )] = rxx( )] = rxx( )p2T( )p2T( ), ), |
(B.-2.06) |
onde
p2T( )
mathend000# é uma função porta de amplitude unitária abrangendo o intervalo [- T, T]
mathend000#. Podemos dizer, neste caso, que
)
mathend000# é uma função porta de amplitude unitária abrangendo o intervalo [- T, T]
mathend000#. Podemos dizer, neste caso, que
 (
( )
mathend000# é um estimador não enviesado de
rxx(
)
mathend000# é um estimador não enviesado de
rxx( )
mathend000# no intervalo [- T, T]
mathend000#. Neste caso, visto que o estimador é não enviesado,
MSE[
)
mathend000# no intervalo [- T, T]
mathend000#. Neste caso, visto que o estimador é não enviesado,
MSE[ (
( )] = V[
)] = V[ (
( )]
mathend000#. No entanto o cálculo de
V[
)]
mathend000#. No entanto o cálculo de
V[ (
( )]
mathend000# é bastante complexo pois envolve o cálculo de momentos de x(t)
mathend000# até à ordem 4. Trata-se de um estimador consistente, no que diz respeito à média, pois
)]
mathend000# é bastante complexo pois envolve o cálculo de momentos de x(t)
mathend000# até à ordem 4. Trata-se de um estimador consistente, no que diz respeito à média, pois
Caso discreto
No caso discreto a expressão da função de autocorrelação equivalente a (B-2.1) escreve-se
| rxx[m] = E{x[k + m]x * [k]}, |
(B.-2.08) |
sendo que a sequência discreta x[k]
mathend000# é considerada estacionária e ergódica. Esta relação pode-se escrever
rxx[m] = 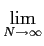 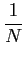  x[n + m]x * [n]. x[n + m]x * [n]. |
(B.-2.09) |
Visto que na prática não dispomos de um intervalo de observação infinito, para nos libertarmos do limite teremos de nos contentar com uma estimativa
 [m]
mathend000# de rxx[m]
mathend000#. As duas formas clássicas de estimar a função de autocorrelação correspondentes à forma enviesada (B-2.2) e à forma não enviesada (B-2.5) são no caso discreto, respectivamente
[m]
mathend000# de rxx[m]
mathend000#. As duas formas clássicas de estimar a função de autocorrelação correspondentes à forma enviesada (B-2.2) e à forma não enviesada (B-2.5) são no caso discreto, respectivamente
 [m] = [m] = 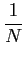  x[n + m]x * [n], m = 0,..., N - 1 x[n + m]x * [n], m = 0,..., N - 1 |
(B.-2.10) |
enquanto que a forma não enviesada é dada por
 [m] = [m] =   x[n + m]x * [n], m = 0,..., N - 1. x[n + m]x * [n], m = 0,..., N - 1. |
(B.-2.11) |
Como a forma enviesada não garante uma DEP definida positiva, i.e., podem-se obter estimativas negativas da DEP, a forma não enviesada é em geral preferida. Como no caso contínuo, ambas as formas são simétricas em relação a m = 0
mathend000#. Sem estarmos a repetir o que já foi dito anteriormente podemos resumidamente lembrar que (B-2.10) tem um viés dado pela função triangular q2N[m]
mathend000#, de base 2N
mathend000#
q2N[m] =  , , |
(B.-2.12) |
mas esse viés desaparece assimptoticamente pois
E{ [m]}
[m]}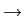 rxx][m]
mathend000# quando
N
rxx][m]
mathend000# quando
N
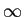 mathend000#; é também um estimador consistente pois que a variância diminui quando o número de amostras aumenta. Para o estimador não enviesado dado por (B-2.11), nota-se que também é consistente, pois a sua variância diminui quando o número de amostras aumenta. Porém demonstra-se que
mathend000#; é também um estimador consistente pois que a variância diminui quando o número de amostras aumenta. Para o estimador não enviesado dado por (B-2.11), nota-se que também é consistente, pois a sua variância diminui quando o número de amostras aumenta. Porém demonstra-se que
V{ [m]} = q2N[m]V{ [m]} = q2N[m]V{ [m]}, [m]}, |
(B.-2.13) |
o que indica que o erro quadrático médio de
 [m]
mathend000# (dado que é um estimador sem viés) tende a ser superior ao de
[m]
mathend000# (dado que é um estimador sem viés) tende a ser superior ao de
 [m]
mathend000#, sobretudo quando m
[m]
mathend000#, sobretudo quando m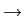 N
mathend000#. Por esta última razão e, apesar do viés, muitos autores preferem utilizar (B-2.10) do que (B-2.11).
N
mathend000#. Por esta última razão e, apesar do viés, muitos autores preferem utilizar (B-2.10) do que (B-2.11).
Método do correlograma
Visto que, em presença de sequências finitas de sinais aleatórios, só é possível obter um estimador da função de autocorrelação, só podemos também obter uma estimativa da DEP de um sinal por aplicação directa do teorema de Wiener-Khintchine. Este tipo de estimador espectral é chamado correlograma pois baseia-se na TF de uma estimativa da função de correlação [6]. Baseando-nos nos dois estimadores da função de autocorrelação propostos no capítulo anterior podemos escrever
 (f )= (f )=   ( ( )e-j2 )e-j2 f f d d , , |
(B.-3.01) |
e que
 (f )= (f )=   ( ( )e-j2 )e-j2 f f d d . . |
(B.-3.02) |
No intuito de determinar o viés destes estimadores espectrais e, usando (B-2.3) e (B-2.6), respectivamente, em (B-3.1) e em (B-3.2), podemos facilmente escrever
E[ (f )] = Pxx(f ) * TF[q2T( (f )] = Pxx(f ) * TF[q2T( )] )] |
(B.-3.03) |
E[ (f )] = Pxx(f ) * TF[p2T( (f )] = Pxx(f ) * TF[p2T( )], )], |
(B.-3.04) |
onde as TF's da função porta e triangular já foram calculadas anteriormente. A partir de (B-3.3) e (B-3.4) podemos deduzir que ambos estimadores
P(1)xx(f )
mathend000# e
P(2)xx(f )
mathend000# são enviesados apesar de só uma das autocorrelações o ser. No entanto, tendo em conta as formas em sin x/x
mathend000# das TF's de
p2T( )
mathend000# e
q2T(
)
mathend000# e
q2T( )
mathend000#, podemos dizer que
)
mathend000#, podemos dizer que
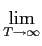 E[ E[ (f )] = Pxx(f ), (f )] = Pxx(f ), |
(B.-3.05) |
e que
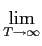 E[ E[ (f )] = Pxx(f ), (f )] = Pxx(f ), |
(B.-3.06) |
o que significa, que para um intervalo de observação suficientemente longo, os dois estimadores produzem resultados sensivelmente iguais e consistentes em relação à média. Pode-se provar ainda que a variância não diminue quando T
mathend000# aumenta e portanto ambos estimadores são inconsistentes em relação à variância. Assim, por exemplo, prova-se que para qualquer T
mathend000#
V[P(2)xx(f )] E[P(2)xx(f )]2. E[P(2)xx(f )]2. |
(B.-3.07) |
A razão deste facto é que os valores de
rxx( )
mathend000# tem uma grande variância para
)
mathend000# tem uma grande variância para  mathend000# próximo de 0 e de T
mathend000#. Isto não depende do valor de T
mathend000#, e a única alternativa para reduzir a variância dos estimadores é de incluir janelas (windows) de observação, com formas particulares, destinadas a diminuir o impacto das amostras junto aos extremos do intervalo de observação.
mathend000# próximo de 0 e de T
mathend000#. Isto não depende do valor de T
mathend000#, e a única alternativa para reduzir a variância dos estimadores é de incluir janelas (windows) de observação, com formas particulares, destinadas a diminuir o impacto das amostras junto aos extremos do intervalo de observação.
Caso discreto
No caso discreto basta calcular a TF da função de autocorrelação discreta que se escreve então
para o estimador enviesado (B-2.10). Como no caso contínuo podemos escrever
E[ ( (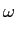 )] = Q2N( )] = Q2N(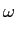 ) * Pxx( ) * Pxx(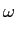 ), ), |
(B.-3.09) |
onde
Q2N(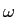 )
mathend000# é a TF da função triangular (B-2.12), o que indica que este estimador do correlograma é também enviesado. Mais interessante é que se utilizarmos o estimador não enviesado da função de autocorrelação (B-2.11) então obtemos
)
mathend000# é a TF da função triangular (B-2.12), o que indica que este estimador do correlograma é também enviesado. Mais interessante é que se utilizarmos o estimador não enviesado da função de autocorrelação (B-2.11) então obtemos
 ( (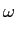 ) = ) =   (m)e-j (m)e-j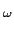 m, M m, M N N |
(B.-3.10) |
de onde se demonstra facilmente que
E[ ( (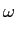 )] = P2M( )] = P2M(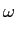 ) * Pxx( ) * Pxx(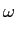 ), ), |
(B.-3.11) |
onde
P2M(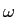 )
mathend000# é a TF da função porta implicitamente utilizada na observação da série temporal num intervalo finito. Quando
N
)
mathend000# é a TF da função porta implicitamente utilizada na observação da série temporal num intervalo finito. Quando
N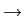
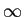 mathend000# as TF de q2N
mathend000# e de p2N
mathend000# ambas tendem para um Dirac (ver sebenta de SS), o que significa que nesse caso temos que a estimativa da DEP tende para o verdadeiro valor e podemos dizer que apesar de enviesadas ambos estimadores são assimptoticamente não enviesados. Porém, existe uma grande diferença entre (B-3.8) e (B-3.10) que é o facto da TF de q2N
mathend000# ser sempre
mathend000# as TF de q2N
mathend000# e de p2N
mathend000# ambas tendem para um Dirac (ver sebenta de SS), o que significa que nesse caso temos que a estimativa da DEP tende para o verdadeiro valor e podemos dizer que apesar de enviesadas ambos estimadores são assimptoticamente não enviesados. Porém, existe uma grande diferença entre (B-3.8) e (B-3.10) que é o facto da TF de q2N
mathend000# ser sempre 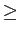 0
mathend000# enquanto a de pN
mathend000# poder ser negativa, resultando a primeira numa DEP sempre positiva enquanto a segunda pode resultar nalguns pontos numa DEP negativa o que é bastante inconsistente com a definição de potência. Na prática costuma-se utilizar valores de M
mathend000# bastante inferiores a N
mathend000# de modo a evitar as fortes oscilações devidas a um aumento do erro quadrático médio como já foi referido. Apesar de a estimada da função de autocorrelação ser assimptoticamente não enviesada e consistente isso não significa que a DEP o seja.
0
mathend000# enquanto a de pN
mathend000# poder ser negativa, resultando a primeira numa DEP sempre positiva enquanto a segunda pode resultar nalguns pontos numa DEP negativa o que é bastante inconsistente com a definição de potência. Na prática costuma-se utilizar valores de M
mathend000# bastante inferiores a N
mathend000# de modo a evitar as fortes oscilações devidas a um aumento do erro quadrático médio como já foi referido. Apesar de a estimada da função de autocorrelação ser assimptoticamente não enviesada e consistente isso não significa que a DEP o seja.
Método do periodograma
Em Sistemas e Sinais mencionámos que outro caminho possível para obter a densidade espectral de potência de um sinal determinístico seria através do cálculo do módulo ao quadrado da sua TF. Quando o sinal é aleatório, do ponto de vista teórico, a sua TF não existe visto que o integral da TF não converge com probabilidade 1. No entanto, num intervalo temporal de observação limitado T
mathend000#, a probabilidade de falta de convergência é praticamente nula e assim X(f )
mathend000#, e portanto a DEP é dada por
PxxT(f )=|XT(f ) , , |
(B.-3.12) |
onde o índice T
mathend000# indica que a observação do sinal é limitada ao tempo T
mathend000#. Este método de cálculo directo toma o nome de sample mean, e foi utilizado durante alguns anos, apesar de dar resultados inconsistentes (ver caso discreto abaixo). Na realidade pode-se provar que a relação que permite obter um resultado equivalente ao do correlograma é o chamado periodograma de Schuster (Schuster's periodogram), dado por
Pxx(f )= 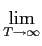 E E 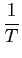 | |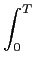 x(t)e-j2 x(t)e-j2 ftdt ftdt ![$\displaystyle \Big]$](img628.png) , , |
(B.-3.13) |
e que não é mais do que dizer que a DEP do sinal x(t)
mathend000# é igual à esperança matemática do módulo ao quadrado da TF de x(t)
mathend000# calculada num intervalo suficientemente longo. Nota-se que, à parte a duração do intervalo, a diferença essencial em relação a (B-3.12) é a introdução da esperança matemática. Podemos efectivamente ver que a relação (B-3.13) se deduz do correlograma da seguinte forma. Desdobrando o módulo ao quadrado a partir de (B-3.13) temos que,
| Pxx(f ) |
= |
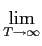 E E 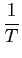 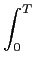 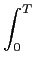 x(t1)x * (t2)e-j2 x(t1)x * (t2)e-j2 f(t1-t2)dt1dt2 f(t1-t2)dt1dt2![$\displaystyle \Big]$](img628.png) , , |
|
| |
= |
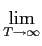 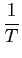 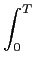 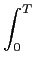 E[x(t1)x * (t2)]e-j2 E[x(t1)x * (t2)]e-j2 f(t1-t2)dt1dt2, f(t1-t2)dt1dt2, |
|
| |
= |
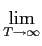 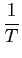 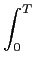 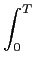 rxx(t1 - t2)e-j2 rxx(t1 - t2)e-j2 f(t1-t2)dt1dt2, f(t1-t2)dt1dt2, |
(B.-3.14) |
onde utilizando a útil integral dupla
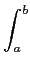 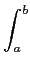 g(t1 - t2)dt1dt2 = (b - a) g(t1 - t2)dt1dt2 = (b - a)  1 - 1 -   g(t)dt, g(t)dt, |
(B.-3.15) |
mencionada em [9] (pag. 115 e seguintes), podemos escrever (B-3.14)
Pxx(f )= 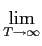   1 - 1 -   rxx( rxx( )e-j2 )e-j2 f f d d . . |
(B.-3.16) |
Quando
T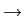
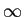 mathend000# a função triangular aproxima-se cada vez mais de uma constante, fazendo com que
mathend000# a função triangular aproxima-se cada vez mais de uma constante, fazendo com que
Pxx(f )= 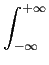 rxx( rxx( )e-j2 )e-j2 f f d d , , |
(B.-3.17) |
o que não é mais do que a densidade espectral de potência obtida através do correlograma (teorema de Wiener-Khintchine).
Caso discreto
A implementação do periodograma no caso discreto faz-se substituindo a TF limitada no tempo pela TFDT também limitada no tempo ou simplesmente pela TFD. Assim a relação (B-3.12) no caso discreto escreve-se
PxxN(f )=| x[n]e-j2 x[n]e-j2 fn fn , , |
(B.-3.18) |
onde agora o índice N
mathend000# indica uma limitação temporal a N
mathend000# amostras.
Claro que esta relação sofre do mesmo problema de instabilidade do que no caso contínuo. Utilizando a mesma demonstração do que no caso contínuo, prova-se que a DEP dado por
Pxx(f )= 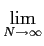 E E 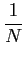 | | x[n]e-j2 x[n]e-j2 fn fn ![$\displaystyle \Big]$](img628.png) , , |
(B.-3.19) |
permite obter efectivamente uma relação idêntica aquela obtida pela TFD da autocorrelação. Para verificar a inconsistência do sample-mean como estimador da DEP, torna-se necessário mencionar alguns resultados respeitantes à sua variância e covariância. Vamos dar o resultado sem demonstração que, apesar de não ser complicada, é um pouco morosa e pode ser encontrada em textos da especialidade, p.ex. em Therrien [10].
Periodograma de Daniell
Neste primeiro método proposto por Daniell (1946), cada frequência  mathend000# do estimador espectral
mathend000# do estimador espectral
 (f )
mathend000# é obtida como a média de 2P
mathend000# frequências adjacentes,
(f )
mathend000# é obtida como a média de 2P
mathend000# frequências adjacentes,
 (fi) = (fi) =    (fi+n), i = P,... (fi+n), i = P,... |
(B.-3.20) |
onde
PxxN(f )
mathend000# é dado por (B-3.18), para o caso discreto. Isto é efectivamente equivalente a filtrar
PxxN(f )
mathend000# por um filtro passa-baixo do tipo média móvel e de função de transferência H(f )
mathend000#,
 (f )= H(f ) * (f )= H(f ) *  (f ). (f ). |
(B.-3.21) |
Calculando a TF inversa de ambos os termos de (B-3.20) obtem-se
 ( ( ) ) |
= |
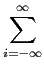   PxxN[(i + n) PxxN[(i + n)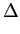 f )ej2 f )ej2 i i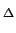 f f , i = 0,... , i = 0,... |
|
| |
= |
  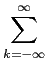 PxxN[k PxxN[k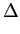 f]ej2 f]ej2 k k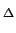 f f e-j2 e-j2 n n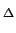 f f , i = 0,... , i = 0,... |
|
| |
= |
   ( ( )e-j2 )e-j2 n n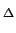 f f , , |
|
| |
= |
 ( ( ) ) e-j e-j 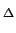 f f  , , |
(B.-3.22) |
e portanto temos que
de onde podemos deduzir que
H(f )= TF[h( )]
mathend000#.
)]
mathend000#.
Periodograma de Bartlett
No método proposto por Bartlett divide-se efectivamente o intervalo N
mathend000# em K
mathend000# intervalos com L
mathend000# amostras cada um, tal que N = KL
mathend000#. Assim se notarmos o sinal x(n)
mathend000# no intervalo k
mathend000# por
| x(k)(n) = x(kL + n), |
(B.-3.24) |
então um estimador do periodograma no intervalo k
mathend000#, escreve-se
 ( (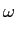 ) = ) = 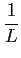 | | x(k)(n)e-j x(k)(n)e-j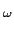 n n , , |
(B.-3.25) |
e finalmente o estimador de Bartlett escreve-se como a média das K
mathend000# DEP's para
0 k
k K - 1
mathend000#,
K - 1
mathend000#,
Demonstra-se facilmente que o estimador de Bartlett tem o mesmo viés que o periodograma mas (como já foi dito anteriormente) a sua variância diminui proporcionalmente com o número de intervalos K
mathend000#, i.e., a estabilidade do estimador aumenta proporcionalmente com K
mathend000#. O único inconveniente é realmente a perda de resolução devido à diminuição do intervalo de observação de N
mathend000# para L
mathend000#.
Em resumo, o método do periodograma de Bartlett procede da seguinte forma:
- partindo de uma sequência temporal discreta x[n]
mathend000# de N
mathend000# amostras, subdividi-la em K
mathend000# sub-intervalos de L
mathend000# amostras cada, tal que N = KL
mathend000#;
- calcular as TFD da série x[n]
mathend000# em cada intervalo de L
mathend000# amostras
- fazer a média dos espectros obtidos ao longo dos K
mathend000# intervalos.
A desvantagem deste procedimento é desde logo evidente na medida em que uma diminuição do intervalo de observação de TN = NTs
mathend000# para
Tk = LTs
mathend000# onde L = N/K
mathend000# faz aumentar Bw
mathend000# para LBw
mathend000#, admitindo um factor Q
mathend000# constante. Assim foram desenvolvidos vários métodos para lidar com o compromisso entre a estabilidade (aumento de K
mathend000#) e resolução (diminuição de Bw
mathend000#). Só esta média vai permitir diminuir a variância do estimador (de um factor K
mathend000# se o ruído for não correlacionado).
Periodograma de Welch
Welch propôs uma versão semelhante ao periodograma de Bartlett no qual utilizou janelas temporais e a possibilidade de sobreposição dos intervalos de estimação dos espectros de ordem k
mathend000#. Se a série temporal
x[n];n = 0,..., N - 1
mathend000# for dividida em K
mathend000# segmentos com L
mathend000# amostras cada, cada segmento está atrasado em relação ao anterior de S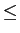 L
mathend000# amostras e então o número de segmentos K
mathend000# é igual à parte inteira de (N - L)/S + 1
mathend000#. No periodograma de Welch o segmento de ordem k
mathend000# é
L
mathend000# amostras e então o número de segmentos K
mathend000# é igual à parte inteira de (N - L)/S + 1
mathend000#. No periodograma de Welch o segmento de ordem k
mathend000# é
| x(k)[n] = w[n]x[n + kS] |
(B.-3.27) |
onde w[n]
mathend000# é a função janela. Em seguida o estimador escreve-se exactamente como o de Bartlett utilizando as K
mathend000# estimativas. As expressões definitivas e mais detalhes podem ser encontrados em Marple [8].
Podemos entretanto notar que o procedimento de Welch permite, para um mesmo valor de N
mathend000#, uma maior estabilidade porque K
mathend000# é mais elevado mantendo uma resolução constante, valor de L
mathend000#. Prova-se além disso (ver Nuthall [7]) que uma sobreposição de 50% oferece o melhor compromisso estabilidade resolução para valores de N
mathend000# e L
mathend000# fixos.
Método combinado periodograma/correlograma
Durante muito tempo tentaram-se outros métodos de forma a unificar o periodograma e o correlograma e se possível evitar as desvantagens de um mantendo as vantagens do outro. Em 1982, Nuthall e Carter propuseram um procedimento baseado no periodograma de Welch mas que inclui o correlograma que simplifica consideravelmente qualquer um dos métodos existentes até aí.
O método combinado proposto por Nuthall e Carter compreende quatro fases: 1) o periodograma de Welch
 (f )
mathend000# é calculado utilizando sobreposição e janelas temporais; 2) é realizada uma TF inversa para obter a autocorrelação de Welch,
(f )
mathend000# é calculado utilizando sobreposição e janelas temporais; 2) é realizada uma TF inversa para obter a autocorrelação de Welch,
 (m)
mathend000#, simétrica e com exactamente 2L + 1
mathend000# pontos; 3) é aplicada uma janela w[m]
mathend000# na função de autocorrelação e 4) realiza-se uma nova TF para obter a DEP do método combinado
(m)
mathend000#, simétrica e com exactamente 2L + 1
mathend000# pontos; 3) é aplicada uma janela w[m]
mathend000# na função de autocorrelação e 4) realiza-se uma nova TF para obter a DEP do método combinado
 (f )
mathend000# tal que
(f )
mathend000# tal que
 (f )= (f )=  (f ) * W(f ), (f ) * W(f ), |
(B.-3.28) |
onde W(f )
mathend000# é a TF da janela temporal aplicada na função de autocorrelação. Torna-se um pouco difícil neste ponto atingir completamente a vantagem de executar esta operação de TF inversa, ponderação e depois uma TF de novo. O facto é que esta segunda ponderação pode ser calculada de modo a modelar o espectro quase à vontade e permitir sobretudo corrigir o viés da DEP e diminuir a variância através do somatório temporal de Welch. Alguns resultados interessantes para o produto estabilidade-tempo-banda-passante para o método combinado encontram-se em Marple [8].
Figura B.1:
sequência temporal T=0.5 s (a) e a DEP estimada com T=5 s tomada como referência (b).
| (a) |
(b) |
![\includegraphics[height=60mm,width=65mm]{figs/tones_time.eps}](img657.png) |
![\includegraphics[height=60mm,width=65mm]{figs/tones_true.eps}](img658.png) |
|
Exemplo: consideremos o registo de um sinal acústico submarino obtido ao largo da Península de Tróia em Abril de 2004, num hidrofone colocado a 60 m de profundidade recebendo um sinal emitido com uma fonte colocada a 75 m de profundidade e a 3 km de distância.
Figura B.2:
correlograma: estimador não enviesado da autocorrelação (a) e respectiva DEP (b), estimador enviesado da autocorrelação (c) e respectiva DEP (d).
|
O objectivo é, a partir de um registo de duração 0.5 segundos determinar uma estimativa do espectro do sinal recebido sabendo que a frequência de amostragem é de 4016 Hz e portanto o número total de pontos é N = 2013
mathend000#. A figura B.1 mostra a sequência temporal observada (a) e a DEP estimada considerando um tempo ``infinito'' (b), assumida como a DEP de referência. Assim podemos notar que o sinal considerado será, em princípio formado por uma soma de 22 sinusoides equiespaçadas entre 900 e 1200 Hz.
Figura B.3:
periodograma: estimador sample-mean(a), Daniell com P = 2
mathend000# (b), Bartlett K = 10
mathend000# e L = 201
mathend000# (c) e Welch L = 1006
mathend000#, K = 3
mathend000#, overlap=50% e uma janela de observação de Hamming (d).
|
|
A figura B.2 mostra em (a) e (b), respectivamente, a estimativa da autocorrelação não enviesada e a respectiva DEP, tomando como horizonte de dados o sinal da figura B.1.
Nota-se que a estrutura da autocorrelação é tipicamente simétrica com o dobro do número de pontos do sinal original. Na DEP nota-se que nem todas as frequências se encontram resolvidas e que a sua amplitude tem uma forte oscilação com um ruído de fundo importante (pedestal oscilante). As figuras (c) e (d) da figura B.2 mostram os resultados obtidos para o estimador enviesado da função de autocorrelação e a DEP correspondente.
Aqui nota-se que a função de autocorrelação é marcadamente diferente comparativamente ao caso anterior, com uma nítida diminuição progressiva da sua amplitude para elevados valores do ``time-lag'', que se deve essencialmente à ausência do factor
1/(T -  )
mathend000# que, quando
)
mathend000# que, quando  mathend000# tende para T
mathend000# tende para valores elevados e contrabalança a diminuição do valor do integral (ou somatório no caso discreto). Nota-se também que a DEP é quase idêntica aquela obtida no caso anterior, o que se justifica pelo facto já referido que a escolha entre os dois estimadores prende-se com razões de consistência do estimador.
A figura B.3 mostra os resultados obtidos nos mesmos dados utilizando os vários estimadores baseados no periodograma: sample-mean (a), Daniell (b), Bartlett (c) e Welch (d). O sample-mean foi obtido através do quadrado do módulo de uma FFT directa do sinal observado. Nota-se que a resolução das sinusoides é relativamente elevada pois todas se encontram presentes. No entanto as suas amplitudes variam fortemente. Uma repetição do sample-mean em intervalos sucessivos do sinal mostra que existe uma grande variabilidade nos valores das frequências tanto em amplitude como e posição no eixo da frequência. No caso (b) obtido com o periodograma de Daniell (P = 2
mathend000#) houve uma clara perda de resolução por média móvel na frequência. Esta perda de resolução torna-se mais evidente no caso (c) obtido com o periodograma de Bartlett com K = 10
mathend000# somatórios no tempo de um sample-mean calculado em L = N/K = 201
mathend000# pontos, sem sobreposição e com uma janela de observação rectangular.
Já no caso da figura B.3(d) foi utilizado um estimador de Welch com
L = N/2 = 1006
mathend000# pontos permitindo uma boa resolução, e ao mesmo tempo uma estabilidade aceitável através de uma média de K = 3
mathend000# sequências obtidas com 50% de sobreposição. Foi também utilizada uma janela de Hamming na ponderação dos dados temporais. A tabela 2.3 mostra um resumo das expressões usuais para os estimadores clássicos da densidade espectral de potência mencionados neste capítulo.
mathend000# tende para T
mathend000# tende para valores elevados e contrabalança a diminuição do valor do integral (ou somatório no caso discreto). Nota-se também que a DEP é quase idêntica aquela obtida no caso anterior, o que se justifica pelo facto já referido que a escolha entre os dois estimadores prende-se com razões de consistência do estimador.
A figura B.3 mostra os resultados obtidos nos mesmos dados utilizando os vários estimadores baseados no periodograma: sample-mean (a), Daniell (b), Bartlett (c) e Welch (d). O sample-mean foi obtido através do quadrado do módulo de uma FFT directa do sinal observado. Nota-se que a resolução das sinusoides é relativamente elevada pois todas se encontram presentes. No entanto as suas amplitudes variam fortemente. Uma repetição do sample-mean em intervalos sucessivos do sinal mostra que existe uma grande variabilidade nos valores das frequências tanto em amplitude como e posição no eixo da frequência. No caso (b) obtido com o periodograma de Daniell (P = 2
mathend000#) houve uma clara perda de resolução por média móvel na frequência. Esta perda de resolução torna-se mais evidente no caso (c) obtido com o periodograma de Bartlett com K = 10
mathend000# somatórios no tempo de um sample-mean calculado em L = N/K = 201
mathend000# pontos, sem sobreposição e com uma janela de observação rectangular.
Já no caso da figura B.3(d) foi utilizado um estimador de Welch com
L = N/2 = 1006
mathend000# pontos permitindo uma boa resolução, e ao mesmo tempo uma estabilidade aceitável através de uma média de K = 3
mathend000# sequências obtidas com 50% de sobreposição. Foi também utilizada uma janela de Hamming na ponderação dos dados temporais. A tabela 2.3 mostra um resumo das expressões usuais para os estimadores clássicos da densidade espectral de potência mencionados neste capítulo.
Sergio Jesus
2008-12-30
![]() )
)
![]()
![]()
![]() 0
0
![]() ) = r(1)xx(
) = r(1)xx(![]() )
)
![]() )
)
![]() ) =
) =  , - T
, - T![]()
![]()
![]() T
T![]() (
(![]() )
)
![]() )
)
![]() E[
E[![]() (
(![]() )]
)]![]()
![]() 1 -
1 - ![]()
![]() rxx(
rxx(![]() )
)![]() ).
).![]() )
)
![]() (
(![]() )
)
![]() )
)
![]() (
(![]() )] = V[
)] = V[![]() (
(![]() )]
)]
![]() (
(![]() )]
)]
![]() E[
E[![]() (
(![]() )] = rxx(
)] = rxx(![]() ).
).![]() [m]
[m]
![]() [m]}
[m]}![]() rxx][m]
rxx][m]
![]()
![]()
![]() [m]} = q2N[m]V{
[m]} = q2N[m]V{![]() [m]},
[m]},![]() [m]
[m]
![]() [m]
[m]
![]() N
N
![]() )
)
![]() )
)
![]() E[
E[![]() (f )] = Pxx(f ),
(f )] = Pxx(f ),![]() E[
E[![]() (f )] = Pxx(f ),
(f )] = Pxx(f ),![]() E[P(2)xx(f )]2.
E[P(2)xx(f )]2.![]() )
)
![]()
![]() (
(![]() )] = Q2N(
)] = Q2N(![]() ) * Pxx(
) * Pxx(![]() ),
),![]() )
)
![]() (
(![]() )] = P2M(
)] = P2M(![]() ) * Pxx(
) * Pxx(![]() ),
),![]() )
)
![]()
![]()
![]() 0
0
![]() E
E![]()
![]()
![]()
![]() x(t1)x * (t2)e-j2
x(t1)x * (t2)e-j2![]() f(t1-t2)dt1dt2
f(t1-t2)dt1dt2![]() ,
,![]()
![]()
![]()
![]() E[x(t1)x * (t2)]e-j2
E[x(t1)x * (t2)]e-j2![]() f(t1-t2)dt1dt2,
f(t1-t2)dt1dt2,![]()
![]()
![]()
![]() rxx(t1 - t2)e-j2
rxx(t1 - t2)e-j2![]() f(t1-t2)dt1dt2,
f(t1-t2)dt1dt2,![]()
![]()
![]()
![]() (f )
(f )
![]() (f )= H(f ) *
(f )= H(f ) * ![]() (f ).
(f ).![]() (
(![]() )
)![]()

![]() PxxN[(i + n)
PxxN[(i + n)![]() f )ej2
f )ej2![]() i
i![]() f
f![]() , i = 0,...
, i = 0,...
![]()
![]() PxxN[k
PxxN[k![]() f]ej2
f]ej2![]() k
k![]() f
f![]() e-j2
e-j2![]() n
n![]() f
f![]() , i = 0,...
, i = 0,...
![]()
![]() (
(![]() )e-j2
)e-j2![]() n
n![]() f
f![]() ,
,![]() (
(![]() )
) e-j
e-j![]()
![]() f
f![]()
 ,
,![]() ) =
) =  e-j
e-j![]()
![]() f
f![]() ,
,![]() )]
)]
![]() (
(![]() ) =
) = ![]() |
|![]() x(k)(n)e-j
x(k)(n)e-j![]() n
n![]() ,
,![]() k
k![]() K - 1
K - 1
![]() (
(![]() ) =
) = ![]()
![]()
![]() (
(![]() ).
).![]() L
L
![]() (f )
(f )
![]() (m)
(m)
![]() (f )
(f )
![]() (f )=
(f )= ![]() (f ) * W(f ),
(f ) * W(f ),![\includegraphics[height=60mm,width=65mm]{figs/tones_time.eps}](img657.png)
![\includegraphics[height=60mm,width=65mm]{figs/tones_true.eps}](img658.png) O objectivo é, a partir de um registo de duração 0.5 segundos determinar uma estimativa do espectro do sinal recebido sabendo que a frequência de amostragem é de 4016 Hz e portanto o número total de pontos é N = 2013
O objectivo é, a partir de um registo de duração 0.5 segundos determinar uma estimativa do espectro do sinal recebido sabendo que a frequência de amostragem é de 4016 Hz e portanto o número total de pontos é N = 2013
![\includegraphics[height=60mm,width=65mm]{figs/tones_corru.eps}](img659.png)
![\includegraphics[height=60mm,width=65mm]{figs/tones_psdu.eps}](img660.png)
![\includegraphics[height=60mm,width=65mm]{figs/tones_corrb.eps}](img661.png)
![\includegraphics[height=60mm,width=65mm]{figs/tones_psdb.eps}](img662.png) A figura B.2 mostra em (a) e (b), respectivamente, a estimativa da autocorrelação não enviesada e a respectiva DEP, tomando como horizonte de dados o sinal da figura B.1.
Nota-se que a estrutura da autocorrelação é tipicamente simétrica com o dobro do número de pontos do sinal original. Na DEP nota-se que nem todas as frequências se encontram resolvidas e que a sua amplitude tem uma forte oscilação com um ruído de fundo importante (pedestal oscilante). As figuras (c) e (d) da figura B.2 mostram os resultados obtidos para o estimador enviesado da função de autocorrelação e a DEP correspondente.
Aqui nota-se que a função de autocorrelação é marcadamente diferente comparativamente ao caso anterior, com uma nítida diminuição progressiva da sua amplitude para elevados valores do ``time-lag'', que se deve essencialmente à ausência do factor
1/(T -
A figura B.2 mostra em (a) e (b), respectivamente, a estimativa da autocorrelação não enviesada e a respectiva DEP, tomando como horizonte de dados o sinal da figura B.1.
Nota-se que a estrutura da autocorrelação é tipicamente simétrica com o dobro do número de pontos do sinal original. Na DEP nota-se que nem todas as frequências se encontram resolvidas e que a sua amplitude tem uma forte oscilação com um ruído de fundo importante (pedestal oscilante). As figuras (c) e (d) da figura B.2 mostram os resultados obtidos para o estimador enviesado da função de autocorrelação e a DEP correspondente.
Aqui nota-se que a função de autocorrelação é marcadamente diferente comparativamente ao caso anterior, com uma nítida diminuição progressiva da sua amplitude para elevados valores do ``time-lag'', que se deve essencialmente à ausência do factor
1/(T - ![\includegraphics[height=60mm,width=65mm]{figs/tones_sm.eps}](img663.png)
![\includegraphics[height=60mm,width=65mm]{figs/tones_dan.eps}](img664.png)
![\includegraphics[height=60mm,width=65mm]{figs/tones_bt.eps}](img665.png)
![\includegraphics[height=60mm,width=65mm]{figs/tones_wlch.eps}](img666.png)
![]() )
)
![]()