Exemplos

Exemplo 1: estabelecer o circuito de Thevenin equivalente para o circuito activo da figura 6.8 ($L_1=5/\omega$ H e $L_2=4/\omega$ H).

Figura 6.8: dipólo indutivo.

Em regime permanente sinusoidal a impedância de Thevenin equivalente escreve-se

$$Z_{th} = jL_1\omega + 5//(3+jL_2\omega)=j5+{{15+20j}\over {8+4j}}=2.5+6.25j$$

Visto que $V_{th}$ é medido em aberto podemos escrever directamente a partir do divisor de tensão

$$\vec V_{th} = {{(3+4j)\vec E}\over {8+j4}}=(0.5 +0.25j)\vec E$$

passando do fasor à componente temporal sabendo que $\vec E = V_m\cos \omega t + j V_m\sin \omega t$

$$\Re\{\vec V_{th}\} = 0.5V_m\cos \omega t - 0.25 V_m \sin \omega t$$

pondo $\cos \phi = 0.5$ e $\sin \phi = 0.25$ e utilizando uma relação trigonométrica usual podemos escrever

$$v_{th}(t) = V_m \cos (\omega t + \phi) \qquad \phi=\tan^{-1}(0.5) = 26.5^{\circ}$$

finalmente o resultado

$$v_{th} = 10 \cos (\omega t + 0.46)$$

$$Z_{th} = 2.5 + 6.25j$$

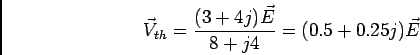
Exemplo 2: considere o circuito representado na figura 6.9.

a) determine a função de transferência $T(j\omega) = V_s/V_e$.

b) traçar no plano de Bode a curva de reposta en frequência deste circuito sabendo que $RC$ = 10$^{-3}$ s/rd.

c) trocando $R$ e $C$ responda de novo às questões a) e b).

d) quais são as propriedades interessantes desta montagem ? O que se passa quando a frequência é mantida fixa e fazemos variar $R$ ?

Figura 6.9: circuito desfasador puro.

Notando $i$ a corrente única no circuito temos as equações nas duas malhas que são

$$\vec V_s + \vec V_e + R \vec I=0\eqno{\rm (a)}$$

$$\vec V_e - \vec V_s + {{\vec I}\over {jC\omega}}=0\eqno{\rm (b)}$$

de (b) podemos deduzir

$$\vec I = jC\omega(\vec V_s - \vec V_e)\eqno{\rm (c)}$$

substituindo (c) em (a) temos

$$\vec V_s(1+jRC\omega) + \vec V_e(1-jRC\omega)=0$$

e finalmente

$$T(j\omega) = {{\vec V_s}\over {\vec V_e}} = - {{1-jRC\omega}\over {1+jRC\omega}}$$

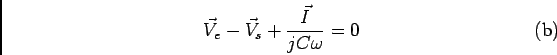
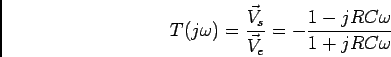
b) o módulo escreve-se

$$\vert T(j\omega) \vert = 1$$

$$\angle T(j\omega) = \tan^{-1} (-RC\omega) - \tan^{-1} (RC\omega)= -2\tan^{-1} (RC\omega)$$

curva de Bode extremamente simples pois o módulo é sempre constante igual a 0 dB enquanto a curva de fase é um arco tangente entre 0 e -180 graus passando a -90 graus para $\omega=\omega_0=1000$ rd/s.

c) o novo circuito encontra-se representado na figura 6.10

Figura 6.10: desfasador puro simétrico.

a partir do qual podemos escrever as equações nas duas malhas

$${{\vec I}\over {jC\omega}} + \vec V_s + \vec V_e = 0$$

$$R\vec I + \vec V_e -\vec V_s = 0$$

tirando $\vec I$ da primeira e substituindo na segunda

$$jRC\omega(-\vec V_s -\vec V_e) + \vec V_e - \vec V_s =0$$

e portanto

$$T(j\omega) = {{\vec V_s}\over {\vec V_e}} = {{1-jRC\omega}\over {1+jRC\omega}}$$

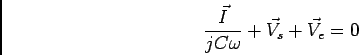
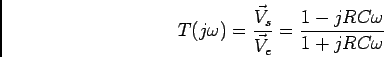
O módulo e a fase de $T(j\omega)$ escrevem-se respectivamente

$$\vert T(j\omega) \vert = 1$$

$$\angle T(j\omega) = -2\tan^{-1} (RC\omega)$$

e o diagrama de Bode é idêntico ao caso precedente.

d) este circuito é um desfasador puro: introduz uma diferença de fase em função da frequência cujo valor se altera modificando a resistência $R$, não introduzindo ganhos nem perdas.