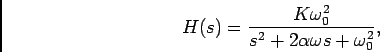 |
(6-6.02) |
Neste caso estaremos em presença, por exemplo, de uma função resposta do tipo (mais uma vez é um exemplo tipo, poderia ser uma função com dois zeros ou um zero e um pólo em vez de dois pólos)
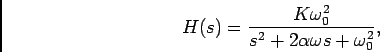 |
(6-6.02) |
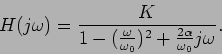 |
(6-6.03) |
Podemos ainda verificar que neste último caso, quando
![]() , que o módulo de
, que o módulo de ![]() tende em dB's para
tende em dB's para
Uma outra característica única da resposta em frequência dos circuitos de segunda ordem é a possível existência de uma sobretensão. Por outras palavras, o valor máximo da função pode não ser obtido nem quando ![]() nem quando
nem quando
![]() . Fazendo o cálculo da derivada em relação a
. Fazendo o cálculo da derivada em relação a ![]() do módulo
do módulo
![]() (que deixamos como exercício) obtemos que essa derivada se anula para
(que deixamos como exercício) obtemos que essa derivada se anula para
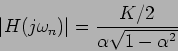
No que diz respeito à fase deste circuito pode-se deduzir fácilmente como sendo variável entre 0 quando ![]() e -180 graus quando
e -180 graus quando
![]() porque a curva de fase é dada por
porque a curva de fase é dada por
