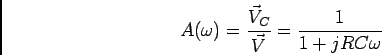 |
(6-5.01) |
No capítulo anterior introduzimos a noção de fasor que é um passo essencial para o uso da notação complexa e a enorme simplificação que esta produz nas equações dos circuitos em regime permanente sinusoidal. Notamos porém, que se esta potente ferramenta de cálculo for utilizada no cálculo intermédio com o objectivo de determinar apenas a resposta temporal, parte da sua economia perde-se no cálculo da parte real do sinal resposta.
Com efeito, esta ferramenta adquire toda sua potencialidade quando se pretende, não obter a resposta temporal, mas sim a resposta frequencial de um determinado circuito. Frequentemente pretendemos determinar qual a resposta de um determinado circuito em regime permanente sinusoidal a diversas frequências do sinal excitação. A este tipo de resposta dá-se o nome de resposta em frequência e é classicamente representada em termos da relação entrada-saída através de diagramas que são: o diagrama de Bode, diagrama cartesiano e diagrama polar ou de Nyquist.
Tomemos como exemplo o caso do circuito RC estudado atrás. A relação entrada-saída pode-se escrever a partir de (6-4.2) como
a) Diagrama de Bode
No diagrama de Bode representa-se o módulo e a fase em gráficos separados sendo a ordenada do módulo em décibeis (dB) e o da fase em graus. Em ambos os casos a abcissa é a frequência em Hz.
O módulo obtem-se no caso de (6-5.1) fazendo
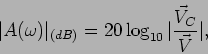 |
(6-5.02) |
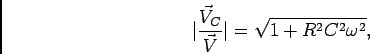 |
(6-5.03) |
| (6-5.04) |
A título de exemplo, as equações (6-5.5) e (6-5.6) encontram-se representadas na figura 6.6 para ![]() rd/s, i.e.,
rd/s, i.e.,
![]() 16.9 Hz.
16.9 Hz.
b) Diagrama cartesiano
No caso do diagrama cartesiano usa-se, como o nome indica, a notação cartesiana de um número complexo. Assim, procura-se colocar a relação entrada-saída sob a forma ![]() . No caso da equação (6-5.1),
. No caso da equação (6-5.1),
| (6-5.07) |
c) Diagrama de Nyquist
Este diagrama utiliza a notação polar complexa na qual um número complexo é representado por um vector cujo comprimento é o módulo de ![]() (eventualmente em dB's) e o ângulo é a fase de
(eventualmente em dB's) e o ângulo é a fase de ![]() parameterizado em
parameterizado em ![]() ou
ou ![]() . i.e.,
. i.e.,
| (6-5.08) |