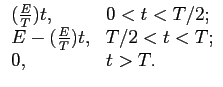
- a)
- representar o sinal de excitação x(t)
mathend000# - b)
- determinar por convolução, a resposta y(t)
mathend000# à excitação x(t) mathend000#.
Exercício 2:
- a)
- demonstre que se F1(s)
mathend000# e F2(S) mathend000# forem respectivamente as Transformadas de Laplace dos sinais f1(t) mathend000# e f2(t) mathend000# então TL[f1(t) * f2(t)] = Fs(s)F2(s)mathend000# - b)
- demonstre que qualquer função x(t)
mathend000# pode ser representada por x(t) =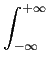 x(
x( )
)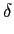 (t -
(t -  )dt
)dt
ondemathend000# 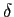 (t)
(t)
mathend000# é o Dirac.
Exercício 3:
Calcule as Transformadas de Fourier dos seguintes sinais
- a)
-
s1(t) = rect(t)
mathend000# - b)
-
s2(t) = sinc(t)
mathend000# - c)
-
s3(t) = exp[- (1/2)(t/
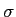 )2]
)2]
mathend000# - d)
-
s4(t) =
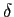 (t)
(t)
mathend000# - e)
- s5(t) = 1
mathend000# - f)
-
s6(t) = u(t)
mathend000# - g)
-
s7(t) = A sin(
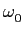 t)
t)
mathend000#
Exercício 4:
Considere o sinal complexo
- a)
- calcule a sua Transformada de Fourier
- b)
- calcule a sua função de autocorrelação
- c)
- calcule a sua densidade espectral de potência
Revisões sobre probabilidades e variáveis aleatórias
Exercício 1:
Considere uma VA X
a) o integral de p(x)
b) a sua variância é também igual a 1.
c) a sua função característica
Exercício 2:
Ao resultado da experiência de jogar uma moeda ao ar associamos uma VA
discreta X
a) qual a esperança matemática E[X]
b) calcular a variância V[X]
c) demonstrar que a função característica da VA X,
Exercício 3:
Uma VA discreta X
a) demonstrar que o momento de ordem 1, m1 = m
b) demonstrar que o momento de ordem 2,
c) calcular as probabilidades
d) calcular a função característica de X
Exercício 4:
Demonstrar que para uma VA Gaussiana X
Exercício 5:
Considere uma combinação linear arbitrária de N
Exercício 6:
A densidade de probabilidade de Cauchy é
a) determine a média e a variância de X
b) determine a função característica de X
Exercício 7:
Uma VA Y
a) determine a função característica de Y
b) detemine a densidade de probabilidade de Y
c) considere a densidade de probabilidade de Y
Exercício 1:
Um sistema ''phase splitter'' é tal que a sua resposta em frequência
se escreve
Exercício 2:
Considere o esquema de blocos da figura D.1, onde y(t)
Exercício 3:
Atendendo a que
H[x(t)] =
Exercício 4:
Considerando o sinal
Exercício 5:
Exercício 6:
Considere o espectro de um sistema realizável h(t)
Determine a parte imaginária X(
Exercício 1:
Considere um processo estocástico Z(t)
Determine igualmente o espectro
PZ(
Exercício 2:
Demonstre que Z(t)
Exercício 3:
Considerando o sinal estocástico complexo
S(t) = R(t) + jI(t)
Exercício 4:
O equivalente em banda base de um sinal PAM passa banda pode-se escrever
a) uma condição suficiente para que
RSS * (
b) que para que (1) seja satisfeita é suficiente que as partes real e
imaginária de Ak
Exercício 5:
Seja
a) demonstre que X(t)
b) demonstre também que sob as condições enumeradas em a) a função
de autocorrelação de X(t)
c) calcule a densidade espectral de X(t)
Exercício 1:
Demonstre que um processo estocástico branco e estacionário Xk
Exercício 2:
Considere um processo estocástico com a seguinte forma
Calcule
a) a média do processo X(t)
b) a função de autocorrelação de X(t)
c) demonstre que X(t)
d) para ma = 0
e) nas mesmas condições que em d) determine a função de autocorrelação média do processo X(t)
f) a partir de
Exercício 3:
Considere um processo estocástico de média nula e estacionário X(t)
a) a expressão da função de autocorrelação de X(n)
b) o valor mínimo de T
c) repita b) para uma densidade espectral de potência de X(t)
Exercício 4:
A função de autocorrelação de um processo estocástico de ruído branco X(t)
Exercício 1:
Considere o seguinte sinal modulador
a) represente graficamente o sinal modulador m(t)
b) calcule o sinal modulado u(t)
c) determine e represente o esboço dos espectros de m(t)
d) determinar a potência do sinal modulador e do sinal modulado
Exercício 2:
Utilizando o mesmo sinal modulador do exercício anterior determinar:
a) a tranformada de Hilbert do sinal modulador m(t)
b) o sinal u(t)
c) a potência do sinal modulador e do sinal modulado.
Exercício 3:
Seja vi(t)
a)
b) a energia do sinal passa banda é igual a
(Ei + Eq)/2
Exercício 4:
Considere o sinal modulador
x(t) = cos(2
a) uma modulação AM-DSB com a = 1
b) uma modulação AM-DSB com a > 1
c) uma modulação CS
Exercício 5:
Provar que para o sinal modulado
Exercício 1:
Considere um sistema PAM em banda base que utiliza impulsos
raised cosine. Fazendo a hipótese de que a sequência a
transmitir é branca e normalizada de forma que o seu
espectro se escreve
demonstre que a potência transmitida é independente de T
Exercício 2:
Considere um canal limitado a
|
Exercício 3:
Considere o seguinte sinal PAM em banda base
No sinal u(t)
a) demonstre que o envelope
|u(t)|
b) determine a densidade espectral de u(t)
Exercício 4:
Considere um sinal 4-PSK definido pelo seu equivalente banda base
a) calcule e represente a densidade espectral de u(t)
b) repita a) com
c) compare os espectros obtidos em a) e b) em termos de largura de
banda a -3 dB e largura de banda no primeiro zero.
truemm
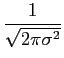 exp
exp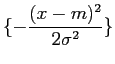
![]() = 1
= 1
![]() (u)
(u)
![]() (u) = jmu +
(u) = jmu + ![]()
![]() = 'coroa
= 'coroa![]() |X = 0) = p
|X = 0) = p
![]() = 'cara
= 'cara![]() |X = 1) = 1 - p = q
|X = 1) = 1 - p = q
![]() (u)
(u)
![]() (u) = 1 + q[exp(ju) - 1]
(u) = 1 + q[exp(ju) - 1]
![]() exp(- m)
exp(- m)![]() (1)
(1)
![]() = m
= m
![]() (u)
(u)
![]()
![]()
![]()
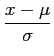
![]()
![]()
![]() = (a12 +...+ aN2)
= (a12 +...+ aN2)![]()
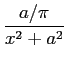 -
- ![]() < x <
< x < ![]()
![]() (1)
(1)
![]()
![]() Xi
Xi
![]()
![]()
Sinais para comunicações
![]() (
(![]() ) =
) = 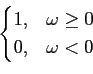
![]() {x(t) + j
{x(t) + j![]() (t)}
(t)}
![]() (t) = H[x(t)]
(t) = H[x(t)]
![]()
![]() (t)
(t)
![]() {y(t) + j
{y(t) + j![]() (t)}e-j
(t)}e-j![]() t
t
![]()
![]() (t)
(t)
![]() (t)] = - x(t)
(t)] = - x(t)
![]() t)
t)
![]() (t)
(t)
![]() (t)]
(t)]
![]() (t)
(t)
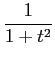
![]() (t)
(t)
![]() ) = R(
) = R(![]() ) + jX(
) + jX(![]() )
)
![]() ) =
) = ![]()
![]() (
(![]() )
)
![]() )
)
Sinais em banda passante
![]() t
t
![]() ) = RS(
) = RS(![]() )ej
)ej![]() t
t
![]() )
)
![]() ) = 0
) = 0
![]() ) = 0
) = 0
![]() ) = 0
) = 0
![]() ) = RI(
) = RI(![]() )
)
![]() ) = - RIR(
) = - RIR(![]() ) = - RRI(
) = - RRI(![]() )
)
![]() Akh(t - kT +
Akh(t - kT + ![]() )
)
![]()
![]()
![]() ) = 0
) = 0
![]() (1)
(1)
![]() Re{Z(t)} =
Re{Z(t)} = ![]() [Z(t) + z * (t)]
[Z(t) + z * (t)]
![]() ) = 0
) = 0
![]() ) = Re{RZ(
) = Re{RZ(![]() )} = Re{ej
)} = Re{ej![]()
![]() RS(
RS(![]() )}
)}
Sinais aleatórios
![]() ang(t - nT)
ang(t - nT)
![]() E[anan+k * ],
E[anan+k * ],
![]() , t)
, t)
![]()
![]() (k)
(k)
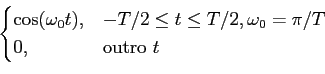
![]() , t)
, t)
![]() (
(![]() ) =
) = ![]()
![]() rxx(t +
rxx(t + ![]() , t)dt
, t)dt
![]() (
(![]() )
)
![]() (f )= TF[rxx(
(f )= TF[rxx(![]() )]
)]
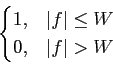
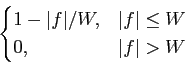
![]() ) =
) = ![]() N0
N0![]() (
(![]() )
)
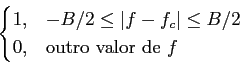
Modulação analógica de onda sinusoidal
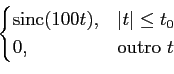
![]() v(t)w * (t)dt =
v(t)w * (t)dt = ![]() V(f )W * (f )df
V(f )W * (f )df
![]() vbp(t)dt = 0
vbp(t)dt = 0
![]() t) - vq(t)sin(
t) - vq(t)sin(![]() t)
t)
![]() f0t)u(t)
f0t)u(t)
![]() t +
t + ![]() )
)
![]()
![]() ]
]
![]() Ac2(1 + a2Sx)
Ac2(1 + a2Sx)
Modulação digital de impulsos
![]() ) = 1
) = 1
![]()
![]() /2
/2![]() |
|![]() 1500
1500
![]() [ang(t - 2nT) - jbng(t - 2nT - T)
[ang(t - 2nT) - jbng(t - 2nT - T)
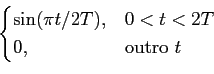
![]() Ing(t - nT)
Ing(t - nT)
![]() (
(![]() 1,
1,![]() j)}
j)}

Sergio Jesus
2008-12-30
![\includegraphics[width=12cm]{figs/td2-1.eps}](img725.png)