



Next: Transformada de Laplace e
Up: Aplicações
Previous: Potência
Contents
Exemplo 1: considere o circuito da figura 3.14:
Figura 3.14:
exemplo de aplicação: 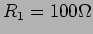 ,
, 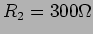 ,
,
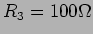 ,
, 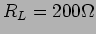 , E=10 V, J=1 A.
, E=10 V, J=1 A.
|
|
Comecemos por aplicar o teorema de sobreposição segundo o qual poderemos dizer que a corrente na carga 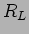 é
é 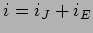 devido às contribuições separadas da fonte de tensão
devido às contribuições separadas da fonte de tensão 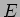 e da fonte de corrente
e da fonte de corrente 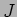 . Temos portanto os esquemas representados em 3.15(a) e 3.15(b) respectivamente. Utilizando o divisor de tensão na figura 3.15(a) temos que
. Temos portanto os esquemas representados em 3.15(a) e 3.15(b) respectivamente. Utilizando o divisor de tensão na figura 3.15(a) temos que
![$i_E R_L = (R_2//R_L) E/[R_1+(R_2//R_L)]$](img242.png) ou seja
ou seja 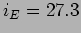 mA. Utilizando agora o divisor de corrente na figura 3.15(b) temos que
mA. Utilizando agora o divisor de corrente na figura 3.15(b) temos que
![$i_J= - (R_1//R_2) J/[R_L+(R_1//R_2)]$](img244.png) , i.e.,
, i.e., 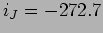 mA, e o teorema de sobreposição diz-nos que
mA, e o teorema de sobreposição diz-nos que
Para poderemos verificar este resultado de forma simples vamos calcular o gerador de Thevenin equivalente entre A e B. Para começar podemos calcular o gerador de Thevenin visto entre os pontos C e D da figura 3.14 e obter a tensão de Thevenin 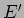 pelo divisor de tensão
pelo divisor de tensão
Figura 3.15:
teorema de sobreposição.
|
|
e a resistência 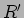
e portanto o esquema equivalente da figura 3.16.
Figura 3.16:
esquema da figura 3.14 simplificado.
|
|
Óbviamente fazendo o cálculo da tensão de Thevenin entre A e B estes dois pontos estarão em aberto e teremos que a corrente que circulará na única malha do circuito será igual a  A. Nesse caso a queda de tensão em
A. Nesse caso a queda de tensão em 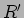 será de
será de 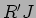 = 75 v e a tensão medida entre A e B tendo em conta o sentido de circulação de
= 75 v e a tensão medida entre A e B tendo em conta o sentido de circulação de 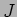 é
é
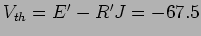 v. A resistência de Thevenin é neste caso
v. A resistência de Thevenin é neste caso
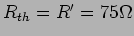 e portanto temos finalmente o circuito equivalente da figura 3.17
e portanto temos finalmente o circuito equivalente da figura 3.17
Figura 3.17:
circuito de Thevenin equivalente.
|
|
da qual se tira fácilmente a corrente 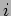 atravessando
atravessando 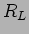 como sendo
como sendo
idêntico ao valor já calculado anteriormente. Utilizando o teorema de Norton, podemos partir da figura 3.16 da qual calculamos a corrente en curto-circuito entre A e B, 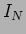 como representado na figura 3.18(a). Observando com atenção esta figura determinamos que
como representado na figura 3.18(a). Observando com atenção esta figura determinamos que 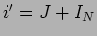 e que
e que
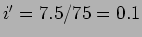 A. Deste modo determinamos
A. Deste modo determinamos 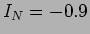 A.
A. 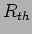 tem evidentemente o mesmo valor de 75
tem evidentemente o mesmo valor de 75  e obtemos o circuito de Norton equivalente da figura 3.18(b)
e obtemos o circuito de Norton equivalente da figura 3.18(b)
Figura 3.18:
circuito simplificado (a) e Norton equivalente (b).
|
|
de onde o divisor de corrente nos permite obter directamente o valor de
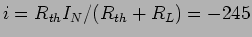 mA.
mA.
Exemplo 2: dado o circuito da figura 3.19, determine 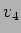 e
e 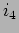 : a) utilizando o teorema de Thevenin e b) utilizando o teorema de Norton.
: a) utilizando o teorema de Thevenin e b) utilizando o teorema de Norton.
a) a resistência equivalente de Thevenin, 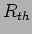 calcula-se desligando a fonte de tensão, i.e., substituindo-a por um curto-circuito e calculando a resistência equivalente "vista" entre A e B que se escreve
calcula-se desligando a fonte de tensão, i.e., substituindo-a por um curto-circuito e calculando a resistência equivalente "vista" entre A e B que se escreve
A tensão equivalente de Thevenin, 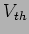 determina-se colocando o circuito em vazio, i.e., retirando a resistência de 1
determina-se colocando o circuito em vazio, i.e., retirando a resistência de 1 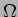 onde passa
onde passa 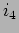 e considerando que a corrente que sai por A é zero. Assim podemos escrever que a corrente
e considerando que a corrente que sai por A é zero. Assim podemos escrever que a corrente 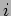 que sai da fonte é igual à corrente
que sai da fonte é igual à corrente 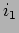 que passa pelas resistências de
que passa pelas resistências de 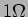 e
e 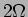 do lado esquerdo, mais a corrente
do lado esquerdo, mais a corrente 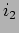 que passa pelas resistências de
que passa pelas resistências de 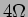 e
e 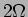 do lado direito.
do lado direito.
sabendo que 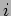 pode ser calculado como
pode ser calculado como
onde 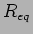 é a resistência equivalente ao total
é a resistência equivalente ao total
deduzimos que 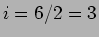 A. Utilizando o divisor de corrente
A. Utilizando o divisor de corrente
e por subtração
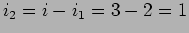 A. Finalmente podemos calcular
A. Finalmente podemos calcular
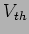 ,
,
A figura 3.20 mostra o circuito de Thevenin equivalente, de onde
podemos escrever que
Figura 3.20:
circuito de Thevenin equivalente.
|
|
b) para calcular o equivalente de Norton basta saber que a resistência equivalente é a mesma que no caso Thevenin e o valor do gerador de corrente 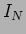 é dado pela corrente em curto circuito entre A e B. Visto que A e B estão ao mesmo potencial podemos escrever que a tensão
é dado pela corrente em curto circuito entre A e B. Visto que A e B estão ao mesmo potencial podemos escrever que a tensão 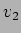 aos bornos das resistências de 2
aos bornos das resistências de 2 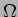 é dado pelo divisor de tensão
é dado pelo divisor de tensão
e então a tensão 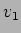 aos bornos da resistência de 4 e 1
aos bornos da resistência de 4 e 1 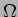 é dada por
é dada por
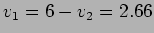 v. A partir daí
v. A partir daí basta determinar a corrente
basta determinar a corrente 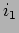 na resistência de 1
na resistência de 1 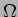
 A, enquanto que a corrente
A, enquanto que a corrente 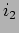 na resistência de 2
na resistência de 2 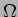 é dada por
é dada por
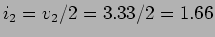 A escrever a lei dos nós tal que
A escrever a lei dos nós tal que
O circuito de Norton equivalente é dado na figura 3.21
Figura 3.21:
circuito de Norton equivalente.
|
|
Óbviamente
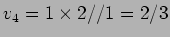 v e
v e
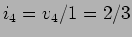 A, mesmo resultado que em a).
A, mesmo resultado que em a).
Exemplo 3: dado o circuito da figura 3.22, calcule o valor da resistência 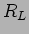 para que as fontes libertem potência máxima em
para que as fontes libertem potência máxima em 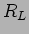 . Calcule também o valor dessa potência máxima (
. Calcule também o valor dessa potência máxima (
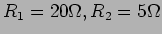 ).
).
Figura 3.22:
circuito Exemplo 3.
|
|
Vamos, por exemplo, começar por determinar o gerador de Thevenin equivalente visto aos terminais de 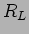 . Segundo a definição o gerador
. Segundo a definição o gerador 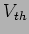 é a tensão medida aos bornos de
é a tensão medida aos bornos de 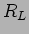 em vazio. Assim, retirando
em vazio. Assim, retirando 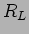 o circuito resume-se a uma única malha na qual podemos calcular a corrente
o circuito resume-se a uma única malha na qual podemos calcular a corrente 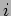 que circula,
que circula,
a partir da corrente podemos calcular a queda de tensão, por exemplo aos
bornos de 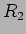 e consecutivamente a tensão
e consecutivamente a tensão 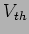 ,
,
por outro lado 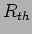 é
é
O circuito equivalente encontra-se na figura 3.23
Figura 3.23:
circuito de Thevenin equivalente ao da figura 3.22.
|
|
Segundo foi demonstrado durante a aula teórica a potência máxima é libertada em 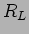 quando
quando
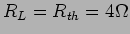 . No caso em que
. No caso em que 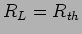 o valor da potência máxima é dado por
o valor da potência máxima é dado por
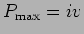 onde
onde
e através do divisor de tensão
e
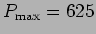 W.
W.
Exemplo 4: Calcule
- a)
- calcule o equivalente de Norton do circuito da figura 3.24 entre A e B.
- b)
- calcule a potência máxima que poderia ser fornecida a uma
resistência
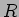 colocada entre A e B
colocada entre A e B
- c)
- que valor deverá ter
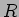 para a potência ser máxima
para a potência ser máxima
Figura 3.24:
circuito Exemplo 4.
|
|
a) comecemos pela resistência equivalente
 . Agora para a corrente de Norton
. Agora para a corrente de Norton 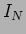 no curto circuito entre A e B podemos fazer utilizando o teorema de sobreposição
no curto circuito entre A e B podemos fazer utilizando o teorema de sobreposição
para 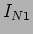 temos o circuito da figura 3.25(a) uma vez que desligada a fonte de tensão ou ainda o circuito da figura 3.25(b) visto que a resistência de 12
temos o circuito da figura 3.25(a) uma vez que desligada a fonte de tensão ou ainda o circuito da figura 3.25(b) visto que a resistência de 12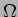 se encontra curto circuitada.
se encontra curto circuitada.
Figura 3.25:
circuitos simplificados do da figura 3.24: desligando a fonte de tensão (a) e simplificando a resistência de
12 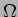 (b).
(b).
|
|
A partir da figura 3.25(b) podemos dizer que 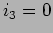 e portanto que
e portanto que 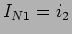 e através do divisor de corrente
e através do divisor de corrente
Para 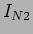 devemos desligar, i.e., substituir por um circuito aberto, o gerador de corrente de 18 A obtendo assim o circuito da figura 3.26(a),
devemos desligar, i.e., substituir por um circuito aberto, o gerador de corrente de 18 A obtendo assim o circuito da figura 3.26(a),
Figura 3.26:
circuitos simplificados do da figura 3.24: desligando a fonte de corrente (a) e simplificando as resistências de
1 e 2 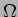 (b).
(b).
|
|
mas como as resistências de 1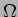 e 2
e 2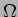 se encontram curto circuitadas podemos deduzir o esquema equivalente da figura 3.26(b). Deste último podemos escrever directamente
se encontram curto circuitadas podemos deduzir o esquema equivalente da figura 3.26(b). Deste último podemos escrever directamente 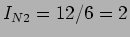 A. Daí
A. Daí que
que 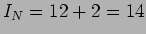 A, obtendo o circuito de Norton equivalente da figura 3.27.
A, obtendo o circuito de Norton equivalente da figura 3.27.
Figura 3.27:
circuito de Norton equivalente.
|
|
b) a potência debitada numa resistência 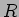 colocada entre A e B é
colocada entre A e B é 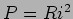 onde a corrente
onde a corrente 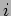 pode ser calculada através do divisor de corrente
pode ser calculada através do divisor de corrente
e então a potência
c) a potência máxima obtem-se quando
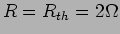 , substituindo na relação anterior temos
, substituindo na relação anterior temos
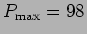 W.
W.




Next: Transformada de Laplace e
Up: Aplicações
Previous: Potência
Contents
Sergio Jesus
2003-12-07
![\includegraphics[width=8cm]{figs/fig3-7.eps}](img239.png)
![]() é
é ![]() devido às contribuições separadas da fonte de tensão
devido às contribuições separadas da fonte de tensão ![]() e da fonte de corrente
e da fonte de corrente ![]() . Temos portanto os esquemas representados em 3.15(a) e 3.15(b) respectivamente. Utilizando o divisor de tensão na figura 3.15(a) temos que
. Temos portanto os esquemas representados em 3.15(a) e 3.15(b) respectivamente. Utilizando o divisor de tensão na figura 3.15(a) temos que
![]() ou seja
ou seja ![]() mA. Utilizando agora o divisor de corrente na figura 3.15(b) temos que
mA. Utilizando agora o divisor de corrente na figura 3.15(b) temos que
![]() , i.e.,
, i.e., ![]() mA, e o teorema de sobreposição diz-nos que
mA, e o teorema de sobreposição diz-nos que
![]() A. Nesse caso a queda de tensão em
A. Nesse caso a queda de tensão em ![]() será de
será de ![]() = 75 v e a tensão medida entre A e B tendo em conta o sentido de circulação de
= 75 v e a tensão medida entre A e B tendo em conta o sentido de circulação de ![]() é
é
![]() v. A resistência de Thevenin é neste caso
v. A resistência de Thevenin é neste caso
![]() e portanto temos finalmente o circuito equivalente da figura 3.17
e portanto temos finalmente o circuito equivalente da figura 3.17
![]() atravessando
atravessando ![]() como sendo
como sendo
![]() mA.
mA.
![]() e
e ![]() : a) utilizando o teorema de Thevenin e b) utilizando o teorema de Norton.
: a) utilizando o teorema de Thevenin e b) utilizando o teorema de Norton.
![]() calcula-se desligando a fonte de tensão, i.e., substituindo-a por um curto-circuito e calculando a resistência equivalente "vista" entre A e B que se escreve
calcula-se desligando a fonte de tensão, i.e., substituindo-a por um curto-circuito e calculando a resistência equivalente "vista" entre A e B que se escreve
![]() determina-se colocando o circuito em vazio, i.e., retirando a resistência de 1
determina-se colocando o circuito em vazio, i.e., retirando a resistência de 1 ![]() onde passa
onde passa ![]() e considerando que a corrente que sai por A é zero. Assim podemos escrever que a corrente
e considerando que a corrente que sai por A é zero. Assim podemos escrever que a corrente ![]() que sai da fonte é igual à corrente
que sai da fonte é igual à corrente ![]() que passa pelas resistências de
que passa pelas resistências de ![]() e
e ![]() do lado esquerdo, mais a corrente
do lado esquerdo, mais a corrente ![]() que passa pelas resistências de
que passa pelas resistências de ![]() e
e ![]() do lado direito.
do lado direito.
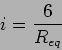
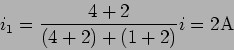
![]() é dado pela corrente em curto circuito entre A e B. Visto que A e B estão ao mesmo potencial podemos escrever que a tensão
é dado pela corrente em curto circuito entre A e B. Visto que A e B estão ao mesmo potencial podemos escrever que a tensão ![]() aos bornos das resistências de 2
aos bornos das resistências de 2 ![]() é dado pelo divisor de tensão
é dado pelo divisor de tensão
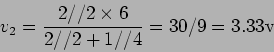
![]() v e
v e
![]() A, mesmo resultado que em a).
A, mesmo resultado que em a).
![]() para que as fontes libertem potência máxima em
para que as fontes libertem potência máxima em ![]() . Calcule também o valor dessa potência máxima (
. Calcule também o valor dessa potência máxima (
![]() ).
).
![]() . Segundo a definição o gerador
. Segundo a definição o gerador ![]() é a tensão medida aos bornos de
é a tensão medida aos bornos de ![]() em vazio. Assim, retirando
em vazio. Assim, retirando ![]() o circuito resume-se a uma única malha na qual podemos calcular a corrente
o circuito resume-se a uma única malha na qual podemos calcular a corrente ![]() que circula,
que circula,
![]() . Agora para a corrente de Norton
. Agora para a corrente de Norton ![]() no curto circuito entre A e B podemos fazer utilizando o teorema de sobreposição
no curto circuito entre A e B podemos fazer utilizando o teorema de sobreposição
![\includegraphics[width=12cm]{figs/fex-5.eps}](img307.png)
![\includegraphics[width=12cm]{figs/fex-6.eps}](img312.png)
![]() colocada entre A e B é
colocada entre A e B é ![]() onde a corrente
onde a corrente ![]() pode ser calculada através do divisor de corrente
pode ser calculada através do divisor de corrente
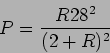
![]() , substituindo na relação anterior temos
, substituindo na relação anterior temos
![]() W.
W.