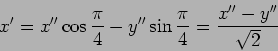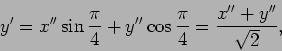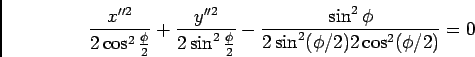Next: Trabalho prático
Up: Instrumentos e técnicas de
Previous: Instrumentos e técnicas de
Contents
Medida de diferenças de fase com o método da elipse
Consideremos dois sinais sinusoidais aplicados nos canais X e Y de um
osciloscópio (eixos ortogonais OX e OY da figura E.11),
A composição destas duas equações obtem-se eliminando o tempo
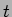 entre elas, i.e., o ponto luminoso no ecrã vai ser desviado
horizontal e verticalmente em simultâneo, formando assim uma figura
parameterizada pela variável tempo.
entre elas, i.e., o ponto luminoso no ecrã vai ser desviado
horizontal e verticalmente em simultâneo, formando assim uma figura
parameterizada pela variável tempo.
- a)
- óbviamente se calcularmos
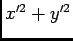 , obtemos
, obtemos
somando e subtraindo
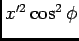 do lado direito da equação obtemos
do lado direito da equação obtemos
visto que o segundo mais o último termo dão 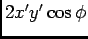 , podemos
escrever
, podemos
escrever
onde substituindo
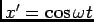 no segundo membro e pondo
no segundo membro e pondo
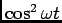 em factor temos
em factor temos
e ainda
e finalmente a relação esperada
- b)
- fazendo agora a mudança de variável
na equação final do ponto a) obtem-se
ou ainda
desenvolvendo e reagrupando os termos em 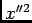 e
e 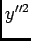 temos
ainda que
temos
ainda que
onde sabendo que
podemos escrever
e finalmente dividindo por
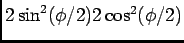 e simplificando
e simplificando
onde podemos reconher que o terceiro termo é efectivamente igual a 1 e
daía equação pretendida.
- c)
- fácilmente deduzimos que
e finalmente




Next: Trabalho prático
Up: Instrumentos e técnicas de
Previous: Instrumentos e técnicas de
Contents
Sergio Jesus
2003-12-07