



Next: Trabalho prático
Up: Filtros RC/CR em regime
Previous: Filtros RC/CR em regime
Contents
1. Revisões: notação complexa
Em regime permanente sinusoidal uma tensão em qualquer ponto de um
circuito pode ser representada por
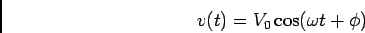 |
(E.-8.1) |
e caracterizada completamente através da sua amplitude 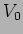 e fase
e fase 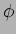 ,
Para efeitos de cálculo, podemos representar o sinal
,
Para efeitos de cálculo, podemos representar o sinal 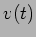 pelo valor
complexo
pelo valor
complexo
 |
(E.-8.2) |
que é um número que pode ser representar no plano complexo como
indicado na figura E.19.
Figura E.19:
representação de fasor.
|
|
A passagem da notação complexa 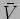 à notação
trigonométrica
à notação
trigonométrica 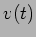 faz-se multiplicando
faz-se multiplicando 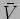 por
por 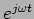 e
tomando a parte real do resultado obtido.
A valor
e
tomando a parte real do resultado obtido.
A valor 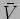 obedece a todas as regras de cálculo dos números
complexos e representa um potente utensílio na análise de circuitos
em regime permanente sinusoidal (e só nesse caso!).
obedece a todas as regras de cálculo dos números
complexos e representa um potente utensílio na análise de circuitos
em regime permanente sinusoidal (e só nesse caso!).
Se aplicarmos uma tensão sinusoidal
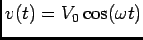 aos terminais
de uma resistência
aos terminais
de uma resistência 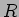 obtemos uma corrente
obtemos uma corrente 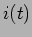 também sinusoidal
de amplitude
também sinusoidal
de amplitude 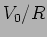 e em fase com
e em fase com 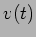 . Em notação complexa podemos
dizer que
. Em notação complexa podemos
dizer que
 |
(E.-8.3) |
Se em vez da resistência tivermos um condensador  , podemos
escrever que
, podemos
escrever que
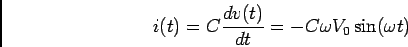 |
(E.-8.4) |
Utilizando a relação
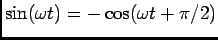 , podemos escrever em notação complexa que o fasor associado com a tensão sinusoidal
, podemos escrever em notação complexa que o fasor associado com a tensão sinusoidal
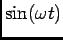 se escreve
se escreve
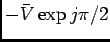 . Substituindo em (E-8.4) temos que
. Substituindo em (E-8.4) temos que
de onde
 |
(E.-8.7) |
Diz-se que um condensador tem uma impedância equivalente em sinusoidal
igual a
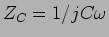 e que a tensão tem um atraso de fase de
e que a tensão tem um atraso de fase de 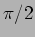 em relação à corrente. No caso da bobine de valor
em relação à corrente. No caso da bobine de valor 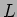 temos que
temos que
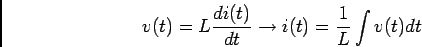 |
(E.-8.8) |
substituindo 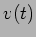
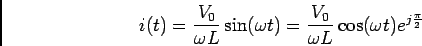 |
(E.-8.9) |
e finalmente
 |
(E.-8.10) |
e diz-se neste caso que a impedância equivalente a uma bobine em regime
sinusoidal permanente é 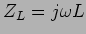 e que a tensão tem um
avanço de fase de
e que a tensão tem um
avanço de fase de 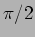 em relação à corrente. Destas duas expressões
em relação à corrente. Destas duas expressões 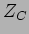 e
e 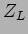 pode ver-se que a impedância da bobine aumenta com a frequência e a do condensador diminui com a frequência.
pode ver-se que a impedância da bobine aumenta com a frequência e a do condensador diminui com a frequência.
2. Revisões: representação de Bode
Um sistema, dito de primeira ordem, tem uma representação
do tipo
onde 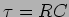 é a constante de tempo do sistema. O estudo
em regime permanente sinusoidal deste sistema faz-se normalmente
através da representação de
é a constante de tempo do sistema. O estudo
em regime permanente sinusoidal deste sistema faz-se normalmente
através da representação de  num diagrama da Bode,
i.e., representando separadamente a amplitude (em dB)
e a fase de
num diagrama da Bode,
i.e., representando separadamente a amplitude (em dB)
e a fase de  .
.
O ganho em décibeis (dB) obtem-se a partir do módulo 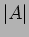 como
como
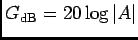 e assim,
e assim,
ou seja
Quando 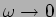 temos que
temos que
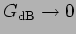 dB e quando
dB e quando
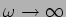 temos que
temos que
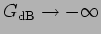 dB.
dB.
A inclinação das assímptotas é de 0 dB quando 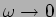 e
de -20 dB por década (passagem de uma frequência
e
de -20 dB por década (passagem de uma frequência 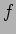 a uma frequência
10
a uma frequência
10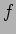 ) quando
) quando
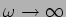 . Isto pode-se determinar observando que quando
. Isto pode-se determinar observando que quando
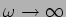
onde
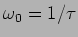 . Num gráfico semi-logarítmico podemos escrever
. Num gráfico semi-logarítmico podemos escrever
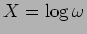 e
e
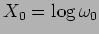 portanto
portanto
o que não é mais do que a equação de uma recta de
inclinação -20 dB e de ordenada na origem igual a
20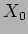 . A função
. A função 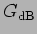 e as respectivas
assímptotas estão representadas na figura E.20.
e as respectivas
assímptotas estão representadas na figura E.20.
Figura E.20:
diagrama de amplitude.
|
|
Define-se a banda passante B como sendo a gama de frequências para
as quais o ganho 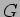 está compreendido entre o seu valor máximo
está compreendido entre o seu valor máximo
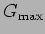 e
e
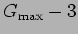 dB. No caso do filtro RC representado
acima, o valor
dB. No caso do filtro RC representado
acima, o valor 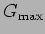 é igual a 0 dB que é atingido para
é igual a 0 dB que é atingido para
 . Por outro lado como -3 dB = -20
. Por outro lado como -3 dB = -20 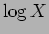 implica
implica 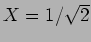 ,
podemos calcular o valor de
,
podemos calcular o valor de 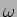 para o qual
para o qual
que tem como solução
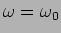 . O resultado final é que a
banda passante B=
. O resultado final é que a
banda passante B=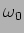 .
.
A diferença de fase entre 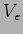 e
e 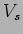 é o argumento do
número complexo
é o argumento do
número complexo 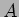 em função da frequência. O argumento
de
em função da frequência. O argumento
de 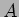 pode-se obter calculando o argumento do numerador e do
denominador (
pode-se obter calculando o argumento do numerador e do
denominador (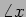 significa ``argumento de
significa ``argumento de 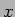 '')
'')
sabendo que o argumento dum número real é zero podemos escrever
pondo
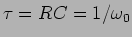 que é a constante de tempo do
circuito.
que é a constante de tempo do
circuito.
Figura E.21:
diagrama de fase.
|
|
Obtemos
A variação de 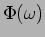 pode-se calcular de forma aproximada observando que quando
pode-se calcular de forma aproximada observando que quando 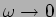
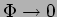 , e que quando
, e que quando
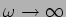 então
então
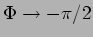 . Obtem-se um valor particular para
. Obtem-se um valor particular para
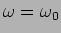 para o qual
para o qual
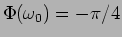 . Podemos fazer um traçado aproximado que terá uma forma semelhante ao da figura E.21. Alguns autores admitem um traçado de fase assímptotico através de segmentos de recta, no qual a fase é considerada nula para
. Podemos fazer um traçado aproximado que terá uma forma semelhante ao da figura E.21. Alguns autores admitem um traçado de fase assímptotico através de segmentos de recta, no qual a fase é considerada nula para
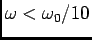 e igual a
e igual a 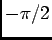 para
para
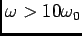 . Para
. Para
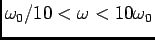 a curva de fase é aproximada por um segmento de recta com uma inclinação de
a curva de fase é aproximada por um segmento de recta com uma inclinação de 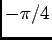 por década.
por década.
3. Estudo de uma célula RC
Considere a montagem da figura E.22 com
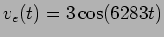
- a)
- desenhar a tensão de saída
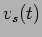 com
com 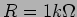 e
e
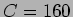 nF.
nF.
- b)
- desenhar a corrente
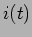 no circuito para a mesma tensão
de entrada
no circuito para a mesma tensão
de entrada 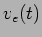 e nas mesmas condições que em a)
e nas mesmas condições que em a)
- c)
- calcule e represente a curva de Bode (amplitude e fase) do ganho em
tensão
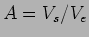 .
.
4. Estudo de uma célula CR
Considere a montagem da figura E.23.
Figura:
circuito CR: 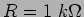 e
e 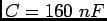 .
.
|
|
- a)
- desenhar a tensão de saída
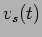 .
.
- b)
- desenhar a corrente
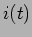 no circuito para a mesma tensão
de entrada
no circuito para a mesma tensão
de entrada 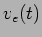 e nas mesmas condições que em a).
e nas mesmas condições que em a).
- c)
- calcule e represente a curva de Bode (amplitude e fase) do ganho em
tensão
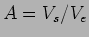 .
.




Next: Trabalho prático
Up: Filtros RC/CR em regime
Previous: Filtros RC/CR em regime
Contents
Sergio Jesus
2003-12-07
![]() à notação
trigonométrica
à notação
trigonométrica ![]() faz-se multiplicando
faz-se multiplicando ![]() por
por ![]() e
tomando a parte real do resultado obtido.
A valor
e
tomando a parte real do resultado obtido.
A valor ![]() obedece a todas as regras de cálculo dos números
complexos e representa um potente utensílio na análise de circuitos
em regime permanente sinusoidal (e só nesse caso!).
obedece a todas as regras de cálculo dos números
complexos e representa um potente utensílio na análise de circuitos
em regime permanente sinusoidal (e só nesse caso!).
![]() aos terminais
de uma resistência
aos terminais
de uma resistência ![]() obtemos uma corrente
obtemos uma corrente ![]() também sinusoidal
de amplitude
também sinusoidal
de amplitude ![]() e em fase com
e em fase com ![]() . Em notação complexa podemos
dizer que
. Em notação complexa podemos
dizer que
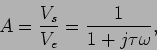
![]() como
como
![]() e assim,
e assim,
![]() e
de -20 dB por década (passagem de uma frequência
e
de -20 dB por década (passagem de uma frequência ![]() a uma frequência
10
a uma frequência
10![]() ) quando
) quando
![]() . Isto pode-se determinar observando que quando
. Isto pode-se determinar observando que quando
![]()
![]() está compreendido entre o seu valor máximo
está compreendido entre o seu valor máximo
![]() e
e
![]() dB. No caso do filtro RC representado
acima, o valor
dB. No caso do filtro RC representado
acima, o valor ![]() é igual a 0 dB que é atingido para
é igual a 0 dB que é atingido para
![]() . Por outro lado como -3 dB = -20
. Por outro lado como -3 dB = -20 ![]() implica
implica ![]() ,
podemos calcular o valor de
,
podemos calcular o valor de ![]() para o qual
para o qual
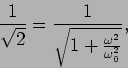
![]() e
e ![]() é o argumento do
número complexo
é o argumento do
número complexo ![]() em função da frequência. O argumento
de
em função da frequência. O argumento
de ![]() pode-se obter calculando o argumento do numerador e do
denominador (
pode-se obter calculando o argumento do numerador e do
denominador (![]() significa ``argumento de
significa ``argumento de ![]() '')
'')
![]()