mathend000#.
Antes de passar à síntese de filtros propriamente dita convém primeiro caracterizar os vários sistemas em dois grandes grupos que são os sistemas sem distorção (capítulo 5.1) e os sistemas com distorção (capítulos seguintes). Os filtros enquadram-se neste último grupo que ainda se pode subdividir, para facilitar o seu estudo, em sistemas só com distorção de amplitude (capítulo 5.2) e sistemas só com distorção de fase (capítulo 5.3). Os filtros em geral são sistemas com distorção de amplitude e de fase. Dentro destes vários grandes grupos, e para clarificar as ideias, convém analisar os sistemas simples de primeira e segunda ordem. Esta análise será feita tanto no domínio do tempo como no da frequência (capítulo 5.4).
A síntese de filtros permite realizar uma função 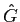 (f )
mathend000#, aproximada de
G(f )= Y(f )/X(f )
mathend000#, de forma prática e económica. A síntese de filtros pode-se dividir em três fases que são: 1) especificação das características do filtro desejado, 2) aproximação das características desejadas por um sistema causal realizável e 3) realização prática do sistema. Nos capítulos 5.6 e 5.7 sobre síntese de filtros FIR e IIR, respectivamente, insistiremos em particular na segunda fase pois a primeira é altamente dependente do utilizador e a terceira prende-se com os aspectos práticos do hardware/software disponível para a concretização do filtro.
(f )
mathend000#, aproximada de
G(f )= Y(f )/X(f )
mathend000#, de forma prática e económica. A síntese de filtros pode-se dividir em três fases que são: 1) especificação das características do filtro desejado, 2) aproximação das características desejadas por um sistema causal realizável e 3) realização prática do sistema. Nos capítulos 5.6 e 5.7 sobre síntese de filtros FIR e IIR, respectivamente, insistiremos em particular na segunda fase pois a primeira é altamente dependente do utilizador e a terceira prende-se com os aspectos práticos do hardware/software disponível para a concretização do filtro.
Um sistema linear é definido como sendo sem distorção quando o sinal de saída y(t)
mathend000# difere do sinal de entrada x(t)
mathend000# no máximo por uma constante H0
mathend000# em amplitude e um atraso t0
mathend000#, ou seja,
|
y(t) = H0x(t - t0).
|
(5-1.01) |
mathend000#
Calculando a TF de ambos os membros de (5-1.1) obtemos
Y( ) = H0X( ) = H0X( )exp(- j )exp(- j t0), t0),
|
(5-1.02) |
mathend000#
ou seja, fazendo aparecer a função de transferência entre entrada e saída,
H( ) = ) = 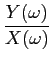 = H0exp(- j = H0exp(- j t0), t0),
|
(5-1.03) |
mathend000#
ou através da TFI a resposta impulsiva
h(t) = H0 (t - t0). (t - t0).
|
(5-1.04) |
mathend000#
A eq. (5-1.3) indica-nos que um sistema sem distorção deverá ter uma amplificação constante em amplitude e uma característica de fase linear. A inclinação da característica de fase é igual ao atraso t0
mathend000#.
Consideremos primeiramente os sistemas de fase linear para nos podermos concentrar na distorção de amplitude. Os sistemas cujo espectro de amplitude da resposta impulsiva atingem valores muito baixos para certas gamas de frequência são chamados filtros. Se
|H( )|
mathend000# tem valores muito baixos para
)|
mathend000# tem valores muito baixos para
 >
> 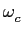 mathend000# diz-se que o filtro H(
mathend000# diz-se que o filtro H( )
mathend000# é um passa-baixo, e que
)
mathend000# é um passa-baixo, e que 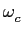 mathend000# é a frequência de corte (ver figura 5.1).
mathend000# é a frequência de corte (ver figura 5.1).
truemm
Figura 5.1:
sistema sem distorção de fase: filtro passa-baixo de fase linear.
|
![\includegraphics[height=50mm]{figs/dist-amplitude.eps}](img399.png) |
Uma noção importante para caracterizar os filtros é a sua largura de banda. Entre as muitas definições utilizadas duas delas são particularmente úteis.
1) a largura de banda B mathend000# pode ser calculada a partir da relação
onde H0
mathend000# é o valor do espectro de amplitude para
mathend000# pode ser calculada a partir da relação
onde H0
mathend000# é o valor do espectro de amplitude para  = 0
mathend000#.
= 0
mathend000#.
2) outra definição muito usual é que define 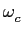 mathend000# pela relação
mathend000# pela relação
H(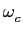 ) = ) = 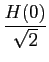 . .
|
(5-2.02) |
mathend000#
o que equivale a escolher 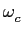 mathend000# tal que
H(
mathend000# tal que
H(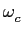 )
mathend000# seja igual ao valor máximo do espectro menos 3 dB.
)
mathend000# seja igual ao valor máximo do espectro menos 3 dB.
determinar a largura de banda da função definida por
|
H(

)|=
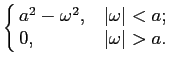
mathend000#
Observando que se trata de uma função par,
mathend000#
e portanto
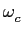 =
= 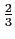 a
mathend000#.
a
mathend000#.
Outra noção importante na caracterização de filtros é a da duração Dt
mathend000# da resposta impulsiva. Assim se tomarmos uma definição análoga à da largura de banda (5-2.1) obtemos que
Dt = 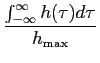 = = 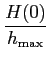 . .
|
(5-2.03) |
mathend000#
Esta definição conduz a uma relação muito interessante entre Dt
mathend000# e
B mathend000# que é
mathend000# que é
Dt = 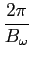 . .
|
(5-2.04) |
mathend000#
A demonstração desta relação obtem-se observando que a TFI da função de transferência é
h(t) = 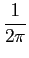  |H( |H( )|e-j )|e-j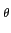 ( ( )ej )ej td td , ,
|
(5-2.05) |
mathend000#
e utilizando o facto de que h(t)
mathend000# deve ser real para um sistema realizável (o que implica que o termo em sin
mathend000# é nulo), então
h(t) = 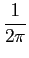  |H( |H( )|cos[ )|cos[ t - t - 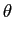 ( ( )]d )]d . .
|
(5-2.06) |
mathend000#
A partir desta última equação deduz-se que o valor máximo da resposta impulsiva se obtem para
cos[ t -
t - 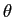 (
( )] = 1
mathend000# o que dá
substituindo a equação (5-2.7) na definição (5-2.3) obtem-se
)] = 1
mathend000# o que dá
substituindo a equação (5-2.7) na definição (5-2.3) obtem-se
Dt = 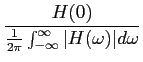 = = 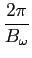 , ,
|
(5-2.08) |
mathend000#
que é a relação procurada, e que indica muito simplesmente, que a duração da resposta impulsiva é inversamente proporcional à banda passante,
Dt = 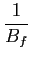 . .
|
(5-2.09) |
mathend000#
É muitas vezes útil conhecer a resposta de um sistema a um degrau unidade (resposta indicial). Quando um sistema cuja resposta impulsiva é h(t)
mathend000# é excitado por um degrau unidade, a resposta pode-se escrever
a(t) = h(t) * u(t) =  h( h( )u(t - )u(t -  )d )d , ,
|
(5-2.10) |
mathend000#
ou seja
o que simplesmente confirma o que já sabíamos a partir de (2-3.57), i.e., que a derivada da resposta indicial é igual à resposta impulsiva. O valor final para
t
 mathend000# pode-se escrever a partir de (5-2.11) e da TF de h(t)
mathend000# no ponto
mathend000# pode-se escrever a partir de (5-2.11) e da TF de h(t)
mathend000# no ponto  = 0
mathend000# como sendo
= 0
mathend000# como sendo
a( ) = ) =  h( h( )d )d = H(0). = H(0).
|
(5-2.12) |
mathend000#
Talvez o mais simples seja passar através da TF de a(t)
mathend000# que é
A( ) = H( ) = H( )U( )U( ) = ) =  H( H( ) ) ( ( ) + ) + 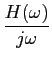 , ,
|
(5-2.13) |
mathend000#
cuja TFI se obtem a partir do espectro de h(t)
mathend000#
a(t) = 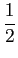  H( H( ) ) ( ( )ej )ej td td + + 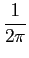  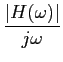 ej[ ej[ (t-t0)]d (t-t0)]d . .
|
(5-2.14) |
mathend000#
O primeiro termo desta expressão é fácil de calcular e dá
H(0) =|H(0)|e0 =|H(0)|/2
mathend000#. No segundo termo podemos considerar
que h(t)
mathend000# é real (e realizável) e por isso dizer que a sua TF é uma função tal que
H(-  ) = H * (
) = H * ( )
mathend000# o que implica que desenvolvendo o segundo termo
)
mathend000# o que implica que desenvolvendo o segundo termo
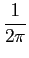  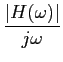 ej[ ej[ (t-t0)]d (t-t0)]d |
= |
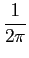  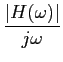 cos[ cos[ (t - t0)]d (t - t0)]d + + |
|
| |
+ |
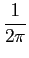  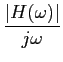 sin[ sin[ (t - t0)]d (t - t0)]d |
|
e dado que o primeiro termo do segundo membro é ímpar e o segundo termo é par (devido à divisão por j mathend000#) integrados num intervalo de
[-
mathend000#) integrados num intervalo de
[- 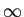 ,
,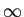 ]
mathend000# faz com que o termo em cos
mathend000# seja nulo, obtendo
]
mathend000# faz com que o termo em cos
mathend000# seja nulo, obtendo
a(t) = 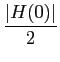 + + 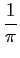 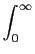 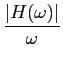 sin[ sin[ (t - t0)]d (t - t0)]d .. ..
|
(5-2.15) |
mathend000#
Esta última relação dá-nos a(t)
mathend000# em função de H( )
mathend000#. Para obter a(t)
mathend000# em função de h(t)
mathend000# teremos que utilizar (5-2.11) e escrever
)
mathend000#. Para obter a(t)
mathend000# em função de h(t)
mathend000# teremos que utilizar (5-2.11) e escrever
a(t) = 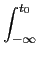 h( h( )d )d + + 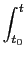 h( h( )d )d , ,
|
(5-2.16) |
mathend000#
de onde utilizando t = t0
mathend000# em (5-2.15), que anula o termo em sin
mathend000#, e o facto que
H(0) = a( )
mathend000# de (5-2.12) temos que
)
mathend000# de (5-2.12) temos que
a(t0) = 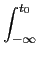 h( h( )d )d = = 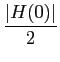 = = 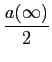 . .
|
(5-2.17) |
mathend000#
truemm
Figura 5.2:
relação entre as respostas impulsiva h(t)
mathend000# e indicial a(t)
mathend000#.
|
![\includegraphics[height=60mm,width=90mm]{figs/impulsiva-indicial.eps}](img423.png) |
Podemos agora determinar alguns parâmetros característicos das respostas impulsiva e indicial muito úteis na caracterização de sistemas lineares. Um deste parâmetros, muito importante em análise transitória, é o tempo de subida tr
mathend000# (rise-time) que é definido como sendo o tempo que o sistema demoara a chegar do estado de repouso ao valor final quando um degrau unidade é colocado à entrada. Pode-se então escrever que o tempo de subida tr
mathend000# depende fortemente do declive P
mathend000# da resposta indicial quando passa do valor inicial para o valor final e escrever
P = 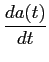 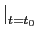 = = 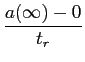 = hmax = h(t0), = hmax = h(t0),
|
(5-2.18) |
mathend000#
visto que hmax
mathend000# é o valor de h(t = t0)
mathend000#. O tempo de subida tr
mathend000# é então dado por
onde Dt
mathend000# é a duração da resposta impulsiva já definida anteriormente. Este resultado não é surpreendente e apenas indica que o sistema é tanto mais rápido (tr
mathend000# mais pequeno) quanto menor for a duração da resposta impulsiva; por seu lado uma resposta impulsiva de menor duração implica uma resposta em frequência com uma maior banda passante como já vimos anteriormente e está bem patente em (5-2.9). A figura 5.2 mostra graficamente as relações entre a(t)
mathend000# e h(t)
mathend000# assim como as definições dos parâmetros característicos.
Um exemplo prático muito frequente de sistemas só com distorção de amplitude é o do filtro passa-baixo ideal, cuja resposta em frequência se encontra representada na figura 5.3.
Figura 5.3:
filtro passa baixo ideal.
|
![\includegraphics[height=50mm]{figs/filtro-pb-ideal.eps}](img427.png) |
O módulo da sua função de transferência escreve-se
enquanto que a característica de fase é
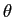 (
( ) = t0
) = t0 mathend000# e portanto a função de transferência é
mathend000# e portanto a função de transferência é
H( ) = H0rect ) = H0rect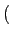 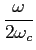 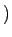 e-j e-j t0, t0,
|
(5-2.21) |
mathend000#
da qual se obtem a resposta impulsiva
h(t) = 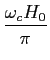 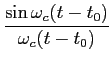 , ,
|
(5-2.22) |
mathend000#
e a resposta ao degrau unidade, utilizando (5-2.21) em (5-2.15) com a mudança de variável
 =
= 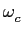 (t - t0)
mathend000#, permite-nos escrever,
(t - t0)
mathend000#, permite-nos escrever,
Da mesma maneira, um sinal x(t)
mathend000# é chamado sinal passa-baixo se
X( ) = 0, |
) = 0, | |>
|> 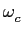 mathend000#. Nesse caso a resposta do filtro H(
mathend000#. Nesse caso a resposta do filtro H( )
mathend000# a este sinal escreve-se
)
mathend000# a este sinal escreve-se
Y( ) = H( ) = H( )X( )X( ) = X( ) = X( )H0e-j )H0e-j t0, t0,
|
(5-2.24) |
mathend000#
e portanto o sinal filtrado é
|
y(t) = H0x(t - t0),
|
(5-2.25) |
mathend000#
o que mostra o facto evidente que o sinal passa-baixo passando num filtro passa-baixo com a mesma frequência de corte não sofre distorção.
Consideramos agora os sistemas cuja característica de fase não é linear mas que mantêm uma característica de amplitude constante em função da frequência. No entanto, mesmo se a fase de tais sistemas já não se pode pôr sobre a forma
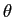 (
( ) =
) =  t0
mathend000#, ela conserva de qualquer maneira o seu caracter de função ímpar, para poder representar sistemas fisicamente realizáveis. O problema da variação de fase é difícil de abordar no caso geral. Consideraremos portanto o caso em que a distorção de fase se pode representar como uma variação
t0
mathend000#, ela conserva de qualquer maneira o seu caracter de função ímpar, para poder representar sistemas fisicamente realizáveis. O problema da variação de fase é difícil de abordar no caso geral. Consideraremos portanto o caso em que a distorção de fase se pode representar como uma variação
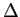
 mathend000# em torno a uma fase linear. Assim a característica de fase de um tal sistema poder-se-á escrever
e a função de transferência
mathend000# em torno a uma fase linear. Assim a característica de fase de um tal sistema poder-se-á escrever
e a função de transferência
H( ) =|H( ) =|H( )|e-j )|e-j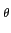 ( ( ) =|H( ) =|H( )|e-j[ )|e-j[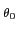 ( ( )+ )+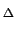 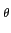 ( ( )], )],
|
(5-3.02) |
mathend000#
ou seja
H( ) = H0( ) = H0( )e-j )e-j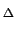 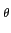 ( ( ), ),
|
(5-3.03) |
mathend000#
onde
H0( )
mathend000# é a resposta em frequência de um sistema sem distorção. O tratamento clássico deste tipo de distorção faz-se considerando que
)
mathend000# é a resposta em frequência de um sistema sem distorção. O tratamento clássico deste tipo de distorção faz-se considerando que
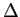
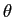 (
( )
) 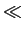 1
mathend000# e então
portanto a equação do sistema transforma-se em
1
mathend000# e então
portanto a equação do sistema transforma-se em
H( ) ) 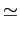 H0( H0( )[1 - j )[1 - j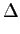 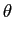 ( ( )]. )].
|
(5-3.05) |
mathend000#
É comum considerar-se que a variação de fase em torno da fase linear é de tipo sinusoidal:
desenvolvendo o seno em soma de exponenciais obtemos
H( ) ) 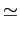 H0( H0( )[1 - )[1 - 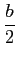 ejn ejn  / /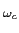 + + 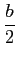 e-jn e-jn  / /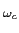 ], ],
|
(5-3.07) |
mathend000#
cuja resposta impulsiva será então
h(t) 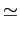 h0(t) - h0(t) - 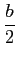 h0(t + h0(t + 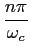 ) + ) + 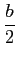 h0(t - h0(t - 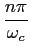 ), ),
|
(5-3.08) |
mathend000#
podendo observar-se o aparecimento de dois sinais eco devido à distorção
de fase.
Se a variação de fase não é pequena em relação a 1, desenvolve-se a exponencial do termo de distorção em série de Fourier no intervalo
(- 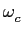 ,
,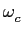 )
mathend000#. Como a fase deve ser uma função ímpar, o desenvolvimento só terá os termos em seno, de forma que
com
obtendo por substituição na equação da função do sistema
)
mathend000#. Como a fase deve ser uma função ímpar, o desenvolvimento só terá os termos em seno, de forma que
com
obtendo por substituição na equação da função do sistema
H( ) = H0( ) = H0( )[J0(b) + J1(b)e )[J0(b) + J1(b)e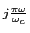 + J-1(b)e + J-1(b)e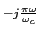 + ...], + ...],
|
(5-3.11) |
mathend000#
onde Jk(b)
mathend000# é a função de Bessel de primeira espécie (ver Abramowitz [4]). Encontramos portanto uma série de ecos espaçados de
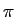 /
/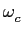 mathend000#.
mathend000#.
Antes de abordarmos a questão dos filtros convém recordar a caracterização dos sistemas mais simples, de primeira e segunda ordem, à luz dos conceitos de representação frequencial e resposta temporal.
A análise frequencial faz-se através do traçado do diagrama de Bode, i.e., aplicando um sinal sinusoidal à entrada x(t)
mathend000# do sistema. Se x(t)
mathend000# é sinusoidal, a saída y(t)
mathend000# também vai ser sinusoidal, porém com um eventual atraso de fase e uma modificação de amplitude. Podemos então escrever a função de transferência
H( ) = ) = 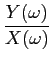 = A( = A( )ej )ej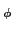 ( ( ), ),
|
(5-4.01) |
mathend000#
a partir da qual o traçado de Bode se faz em dois gráficos, amplitude
em dB
AdB = 20 log
10|
A(

)|=
f (log
10
)
mathend000#
e fase em linear
mathend000#
É frequente considerar intervalos de frequência correspondentes a uma oitava, quando se passa de f1
mathend000# para 2f1
mathend000# ou a uma década quando se passa de f1
mathend000# para 10f1
mathend000#. Uma das vantagens da representação de Bode consiste no facto de dois sistemas H1
mathend000# e H2
mathend000# em série poderem ser representados por um único sistema H
mathend000# cujo módulo é o produto dos módulos e a fase é a soma das fases, resultando em Bode na soma dos diagramas de amplitude e na soma dos diagramas de fase (o logaritmo do produto é a soma dos logaritmos!).
Recorrendo à forma geral (3-10.3) podemos escrever a função de transferência H( )
mathend000# como
)
mathend000# como
H( ) ) |
= |
A( )ej )ej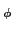 ( ( ) ) |
|
| |
= |
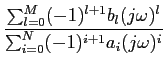 |
|
| |
= |
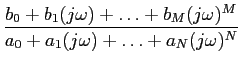 , , |
(5-4.02) |
na qual as raízes do polinómio do numerador são chamados os zeros zl
mathend000# da função de transferência e as raízes do denominador são chamados os pólos pi
mathend000# da função de transferência. Podemos assim escrever
H( ) = K ) = K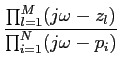 , ,
|
(5-4.03) |
mathend000#
a partir da qual podemos notar que mesmo que os coeficientes al
mathend000# e bi
mathend000# sejam reais os zeros e pólos poderão ser reais ou complexos.
Os sistemas de primeira ordem são caracterizados apenas por um único pólo ou zero reais. Os sistemas de segunda ordem têm dois pólos ou dois zeros que podem ser reais ou complexos. Existe um caso particular que é quando o sistema admite raízes nulas, zl = 0
mathend000# ou pi = 0
mathend000#. Devemos ainda considerar o caso de raízes múltiplas como seja
(j - zi)l
mathend000# para zi
- zi)l
mathend000# para zi 0
mathend000# ou
(j
0
mathend000# ou
(j )l
mathend000# quando zi = 0
mathend000#.
)l
mathend000# quando zi = 0
mathend000#.
1) diagrama de Bode de j mathend000# ou 1/j
mathend000# ou 1/j mathend000#
mathend000#
O diagrama de Bode tipo para os sistemas com raízes nulas encontra-se representado na figura 5.4
Podemos facilmente deduzir que o sistema
(j )l
mathend000# terá uma inclinação em amplitude de
l×20
mathend000# dB/década e uma fase que será
l×90
mathend000# graus. Da mesma forma o sistema
1/(j
)l
mathend000# terá uma inclinação em amplitude de
l×20
mathend000# dB/década e uma fase que será
l×90
mathend000# graus. Da mesma forma o sistema
1/(j )l
mathend000# terá uma inclinação em amplitude de
- l×20
mathend000# dB/década e uma fase que será
- l×90
mathend000# graus.
)l
mathend000# terá uma inclinação em amplitude de
- l×20
mathend000# dB/década e uma fase que será
- l×90
mathend000# graus.
2) diagrama de Bode dos sistemas de primeira ordem
O diagrama de Bode tipo para os sistemas de primeira ordem do tipo
1 + j T
mathend000# ou
1/(1 + j
T
mathend000# ou
1/(1 + j T)
mathend000# tomará a seguinte forma
T)
mathend000# tomará a seguinte forma
|A( ) )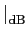 |
= |
20 log10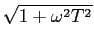 |
|
| |
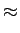 |
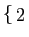 0 log10 0 log10 T T |
(5-4.04) |
ou
|A( ) )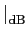 |
= |
-20 log10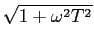 |
|
| |
 |
 20 log10 20 log10 T T |
(5-4.05) |
de onde podemos obter a representação assimptótica para sistemas de primeira ordem representada na figura 5.5.
Figura 5.5:
diagrama de Bode assimptótico de sistemas de primeira ordem.
|
![\includegraphics[height=90mm,width=120mm]{figs/ordem-1.eps}](img461.png) |
De notar que se trata de uma representação assimptótica através de dois segmentos de recta para o módulo e três para a fase, para
 <
< 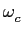 mathend000# e para
mathend000# e para
 >
> 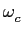 mathend000#, onde
mathend000#, onde
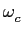 = 1/T
mathend000# é a pulsação de corte do sistema. O erro máximo cometido em amplitude entre a curva real e o diagrama assimptótico é de 3 dB e esse erro máximo encontra-se precisamente quando
= 1/T
mathend000# é a pulsação de corte do sistema. O erro máximo cometido em amplitude entre a curva real e o diagrama assimptótico é de 3 dB e esse erro máximo encontra-se precisamente quando
 =
= 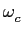 mathend000#. O erro máximo em fase é de cerca de ±
mathend000#6 graus e é cometido a
mathend000#. O erro máximo em fase é de cerca de ±
mathend000#6 graus e é cometido a
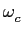 /10
mathend000# e
10
/10
mathend000# e
10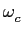 mathend000#.
mathend000#.
3) diagrama de Bode dos sistemas de segunda ordem
Podem-se obter sistemas de ordem 2 ou de ordem superior por simples montagem em série de vários sistemas de primeira ordem. Como já foi dito os diagramas de Bode assimptóticos resultantes deduzem-se facilmente dos diagramas das figuras 5.4 e 5.5. O problema é diferente se as raízes não forem reais. Vejamos, a título de exemplo, o caso de um sistema de 2a
mathend000# ordem com dois pólos complexos conjugados do tipo
onde fizemos o pólo
s1 = 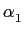 + j
+ j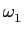 mathend000#. Definindo os coeficientes habituais
mathend000#. Definindo os coeficientes habituais
 = -
= - 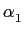 /
/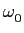 mathend000# e
mathend000# e
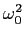 =
= 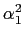 +
+ 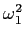 mathend000# e
K =
mathend000# e
K = 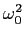 mathend000#, temos
mathend000#, temos
A( ) = ) = 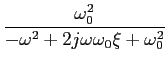 , ,
|
(5-4.07) |
mathend000#
onde 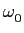 mathend000# é chamada a pulsação do sistema não amortecido e 0
mathend000# é chamada a pulsação do sistema não amortecido e 0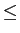
 mathend000# é o coeficiente de amortecimento. Para
mathend000# é o coeficiente de amortecimento. Para  = 0
mathend000# temos um sistema não amortecido, se
= 0
mathend000# temos um sistema não amortecido, se  mathend000# for igual a 1 temos que
mathend000# for igual a 1 temos que
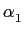 =
= 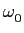 mathend000# o que corresponde ao regime crítico. Se
mathend000# o que corresponde ao regime crítico. Se  > 1
mathend000# temos o regime sobre amortecido e finalmente se
0 <
> 1
mathend000# temos o regime sobre amortecido e finalmente se
0 <  < 1
mathend000# temos o regime sob amortecido. Para uma revisão destes vários regimes de funcionamento ver a sebenta de Análise de Circuitos, capítulo 5, [3]. Podemos então escrever o módulo da resposta em frequência
< 1
mathend000# temos o regime sob amortecido. Para uma revisão destes vários regimes de funcionamento ver a sebenta de Análise de Circuitos, capítulo 5, [3]. Podemos então escrever o módulo da resposta em frequência
|A( )|= )|= 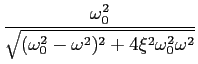 . .
|
(5-4.08) |
mathend000#
O máximo de
|A( )|
mathend000# obtem-se calculando a derivada de (5-4.8) e igualando a zero, o que permite obter (descartando a solução trivial
)|
mathend000# obtem-se calculando a derivada de (5-4.8) e igualando a zero, o que permite obter (descartando a solução trivial 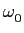 mathend000#) a pulsação
mathend000#) a pulsação 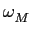 mathend000# correspondente ao máximo que é
que só existirá quando
mathend000# correspondente ao máximo que é
que só existirá quando
 < 1/
< 1/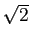 mathend000# ou seja quando
mathend000# ou seja quando
 < 0.707
mathend000#. Isto é, se
0.707 <
< 0.707
mathend000#. Isto é, se
0.707 <  < 1
mathend000# não existe máximo, se
< 1
mathend000# não existe máximo, se
 < 0.707
mathend000# então a curva do módulo tem um máximo, por vezes chamado sobre-tensão, que será tanto mais pronunciada quanto mais pequeno for o valor do coeficiente
< 0.707
mathend000# então a curva do módulo tem um máximo, por vezes chamado sobre-tensão, que será tanto mais pronunciada quanto mais pequeno for o valor do coeficiente  mathend000#, colocando (5-4.9) na expressão do módulo
mathend000#, colocando (5-4.9) na expressão do módulo
|A(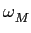 )|= AM = )|= AM = 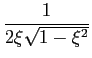 . .
|
(5-4.10) |
mathend000#
Além disso a frequência de ressonância 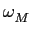 mathend000# desloca-se em função de
mathend000# desloca-se em função de  mathend000# de acordo com a relação (5-4.9) e que será tanto mais inferior a
mathend000# de acordo com a relação (5-4.9) e que será tanto mais inferior a 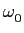 mathend000# quanto maior for
mathend000# quanto maior for  mathend000#, tendendo ao limite para
mathend000#, tendendo ao limite para 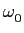 mathend000# quando
mathend000# quando  = 0
mathend000#.
= 0
mathend000#.
A curva de fase obtem-se calculando o argumento da expressão (5-4.7) que se escreve
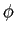 ( ( ) ) |
= |
- 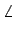 { {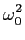 - - 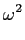 +2j +2j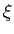 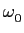  } } |
|
| |
= |
- Arctg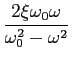 , , |
(5-4.11) |
que varia entre 0 e - 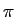 mathend000# quando
mathend000# quando  mathend000# varia de 0 a
mathend000# varia de 0 a 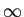 mathend000#. A transição em torno a
mathend000#. A transição em torno a 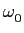 mathend000# é tanto mais brusca quanto menor for o valor de
mathend000# é tanto mais brusca quanto menor for o valor de  mathend000#. O módulo e fase de um sistema de segunda ordem como aquele estudado até aqui encontra-se representado na figura 5.6 para vários valores do coeficiente de amortecimento
mathend000#. O módulo e fase de um sistema de segunda ordem como aquele estudado até aqui encontra-se representado na figura 5.6 para vários valores do coeficiente de amortecimento  mathend000#.
mathend000#.
Já estudámos anteriormente a resposta temporal de vários sistemas seja a um impulso - resposta impulsiva - seja a um degrau unidade - resposta indicial.
1) sistemas de primeira ordem
A função de transferência no domínio de Laplace, por exemplo para um sistema do tipo passa-baixo, escreve-se
H(s) = 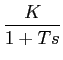 , ,
|
(5-4.12) |
mathend000#
onde K
mathend000# é uma constante real e T
mathend000# é a constante de tempo, de onde podemos calcular a resposta indicial, i.e., a resposta a um sinal de entrada X(s) = 1/s
mathend000#,
A(s) = 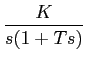 , ,
|
(5-4.13) |
mathend000#
que admite dois pólos, um em zero e o outro em -1/T
mathend000#, obtendo-se uma resposta no domínio do tempo
|
a(t) = K(1 - e-t/T).
|
(5-4.14) |
mathend000#
Esta resposta já foi estudada extensivamente em Análise de Circuitos. Relembramos que a tangente na origem tem inclinação K/T
mathend000#, que a(T) = 2/3K
mathend000# e que o tempo de subida tr
mathend000#, para o qual é atingido 95% do valor final, é
tr 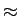 3T
mathend000#.
3T
mathend000#.
2) sistemas de segunda ordem
Utilizando a mesma técnica para um sistema de segunda ordem de função transferência
H(s) = 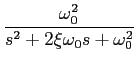 , ,
|
(5-4.15) |
mathend000#
cuja resposta indicial, para X(s) = 1/s
mathend000#, admite três pólos, um igual a zero e dois complexos conjugados
permitindo a seguinte decomposição em fração racional da resposta A(s)
mathend000# ao degrau unidade
A(s) = A/s + 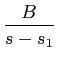 + + 
|
(5-4.17) |
mathend000#
onde, obviamente,
s2 = s1 *
mathend000#. O cálculo dos coeficientes permite-nos deduzir
| A |
= |
1, |
|
| B |
= |
- 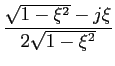 , , |
|
de onde substituindo em (5-4.17) e fazendo a TLI se obtém a relação temporal da resposta indicial
a(t) = 1 - 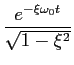 [ [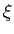 sin( sin(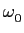 t t ) + ) +  cos( cos(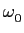 t t )]. )].
|
(5-4.18) |
mathend000#
Fazendo
 = cos
= cos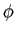 mathend000# e
mathend000# e
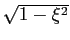 = sin
= sin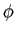 mathend000# e utilizando a relação
sin(a + b) = sin a cos b + sin b cos a
mathend000#, temos que a resposta indicial se pode escrever
mathend000# e utilizando a relação
sin(a + b) = sin a cos b + sin b cos a
mathend000#, temos que a resposta indicial se pode escrever
a(t) = 1 - 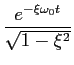 sin( sin(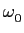 t t + + 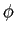 ), ),
|
(5-4.19) |
mathend000#
Figura 5.7:
reposta indicial num sistema de segunda ordem para vários
valores de  mathend000#=0.05, 0.25, 0.5, 0.707 e 0.95.
mathend000#=0.05, 0.25, 0.5, 0.707 e 0.95.
|
![\includegraphics[height=60mm,width=100mm]{figs/ordem_2_t.eps}](img492.png) |
tratando-se de uma resposta oscilatória que ultrapassa o valor final é importante calcular o valor máximo e as abcissas dos máximos e mínimos (ver figura 5.7). Estes obtem-se derivando a(t)
mathend000# e igualando a zero
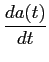 = = 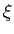 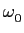 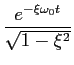 sin( sin(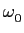 t t + + 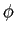 ) - ) - 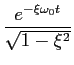 cos( cos(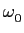 t t + + 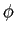 ) )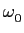  = 0, = 0,
|
(5-4.20) |
mathend000#
implica que
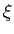 sin( sin(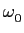 t t + + 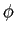 ) = cos( ) = cos(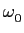 t t + + 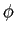 ) ) , ,
|
(5-4.21) |
mathend000#
onde, dado os valores de 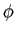 mathend000# permite escrever
mathend000# permite escrever
tan(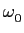  tp + tp + 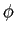 ) = tan ) = tan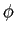 , ,
|
(5-4.22) |
mathend000#
que por sua vez implica
onde tp
mathend000# corresponde ao(s) instante(s) dos máximo(s)/mínimo(s) que se obtem para valores inteiros de k
mathend000# e directamente como sendo
tp = 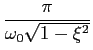 , ,
|
(5-4.24) |
mathend000#
para k = 1
mathend000#, primeiro máximo e por substituição em (5-4.19) obtem-se o valor máximo da resposta nesse instante
ap = 1 + exp(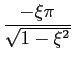 ). ).
|
(5-4.25) |
mathend000#
A partir destas duas últimas equações podemos ver que quanto menor for o valor do coeficiente de amortecimento  mathend000#, mais rápida será a resposta do sistema, tp
mathend000# pequeno, mas por outro lado a ultrapassagem do valor final é maior, ap
mathend000# mais elevado em relação a 1. Isto pode ser verificado graficamente na figura 5.8
mathend000#, mais rápida será a resposta do sistema, tp
mathend000# pequeno, mas por outro lado a ultrapassagem do valor final é maior, ap
mathend000# mais elevado em relação a 1. Isto pode ser verificado graficamente na figura 5.8
Figura 5.8:
valor da ultrapassagem do primeiro máximo da resposta indicial
de um sistema de ordem 2, em percentagem (%) do valor final em função
do coeficiente de amortecimento  mathend000#.
mathend000#.
|
![\includegraphics[height=60mm,width=100mm]{figs/ap_ordem2.eps}](img495.png) |
Podemos agora tecer algumas considerações sobre as relações entre as respostas temporal e frequencial. Relembremos os valores das respostas indiciais calculados nos dois últimos capítulos, em frequência
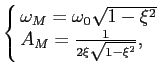
|
(5-4.26) |
mathend000#
e no tempo
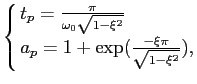
|
(5-4.27) |
mathend000#
portanto podemos concluir que um valor pequeno de  mathend000#, digamos inferior a 0.4 resulta numa forte sobretensão e numa forte ultrapassagem do valor final da resposta temporal. Simultaneamente obtem-se um sistema que responde rapidamente no tempo e que tem uma banda passante estreita na frequência, trata-se por isso de um sistema relativamente selectivo. Existe por isso uma relação estreita entre as respostas frequencial e temporal e o conhecimento tanto de uma como da outra permitem determinar os coeficientes do sistema.
mathend000#, digamos inferior a 0.4 resulta numa forte sobretensão e numa forte ultrapassagem do valor final da resposta temporal. Simultaneamente obtem-se um sistema que responde rapidamente no tempo e que tem uma banda passante estreita na frequência, trata-se por isso de um sistema relativamente selectivo. Existe por isso uma relação estreita entre as respostas frequencial e temporal e o conhecimento tanto de uma como da outra permitem determinar os coeficientes do sistema.
Existe um valor particular  = 0.425
mathend000# para o qual se obtem uma sobretensão de 2.3 dB e uma ultrapassagem de 20% da resposta indicial, que é normalmente aceitável na prática.
= 0.425
mathend000# para o qual se obtem uma sobretensão de 2.3 dB e uma ultrapassagem de 20% da resposta indicial, que é normalmente aceitável na prática.
Caracterizando a resposta em frequência do filtro por
G(f )= Y(f )/X(f )
mathend000#, e uma vez calculada a função G(f )
mathend000#, trata-se em seguida de nos assegurarmos que esta é praticamente realizável por um sistema invariante e ``económico''. Para que o sistema seja realizável é necessário que ele seja causal e estável. Isto é, que num tal sistema, o sinal de saída não poderá preceder o sinal de entrada, e que para um sinal de entrada de energia finita, o sinal de saída também deverá ser de energia finita. Por outro lado, é também necessário que o número de operações seja finito, e que a resposta em frequência seja o mais próxima possível daquela desejada.
Esquematizando, pode-se dizer que os filtros digitais se classificam em dois grandes grupos:
- filtros de resposta impulsiva finita (FIR, finite impulse response)
- filtros de resposta impulsiva infinita (IIR, infinite impulse response)
No caso dos filtros FIR o sinal resposta do filtro obtém-se através de uma equação de convolução discreta do tipo (2-3.41) mas com um número finito de termos N
mathend000# correspondente à duração da resposta impulsiva do filtro e onde h[n]
mathend000#, x[n]
mathend000# e y[k]
mathend000# são versões discretas da resposta impulsiva do filtro e dos sinais de entrada e de saída respectivamente.
Faz ainda parte do tipo de filtros FIR o método da síntese de Fourier. A ideia consiste em transformar o sinal do domínio do tempo para o domínio da frequência, multiplicá-lo pelo filtro, e fazer em seguida uma transformada inversa de novo para o domínio temporal para obter o sinal resposta. Neste caso, a função de transferência não é modificada por erros devidos à limitação da resposta impulsiva ou erros de arredondamento. No entanto, este tipo de implementação sofre dos problemas de limitação temporal do sinal quando da transformação tempo para frequência e vice-versa. Estes problemas foram discutidos abundantemente no capítulo anterior e não serão retomados aqui.
Pelo seu lado, os filtros IIR são geralmente implementados através de uma equação do tipo de (2-7.4) que é uma forma recursiva do sinal de saída y(t)
mathend000# e que não faz nenhuma hipótese de limitação na duração da resposta impulsiva do sistema. O cálculo do filtro resume-se à determinação da ordem N
mathend000# e M
mathend000# das partes AR e MA do filtro e do cálculo dos coeficientes an
mathend000# e bm
mathend000#, de modo a que a função de transferência obedeça à equação (3-10.2).
Antes de analisarmos os métodos de síntese para os filtros FIR e IIR devemos determinar os tipos de filtros que pretendemos realizar e quais os parâmetros que os caracterizam. Como acabámos de dizer, em geral, os filtros são caracterizados pela sua resposta em frequência G(f )
mathend000#. Assim podem ser classificados pelas funções ideais passa-baixo, passa-alto, passa-banda e corta-banda. Acabámos de definir as características e os tipos de filtros ideais, ou seja, aqueles que na banda passante deixam passar tudo sem alteração e cortam absolutamente tudo na banda de corte. Como sabemos tais filtros não são realizáveis, e teremos que definir quais os valores máximos de desvio que se podem admitir entre a realização ideal e a realização prática. Assim somos levados a definir quantidades como por exemplo: oscilação na banda passante, oscilação na banda de corte, largura da banda de transição, etc... Noutras palavras, deveremos definir uma margem de tolerância em torno aos valores ideais que constituem os valores máximos e mínimos a não ultrapassar (figura 5.9).
truemm
Figura 5.9:
margens de tolerância na síntese de filtros.
|
![\includegraphics[width=100mm]{figs/gabarito-filtros.eps}](img498.png) |
A implementação prática dos filtros FIR faz, em geral, apelo à equação de convolução no caso discreto. Este tipo de implementação é possível porque o número de amostras da resposta impulsiva do filtro é tornado finito. A síntese dos filtros FIR faz-se através da resolução da TFI da função G(f )
mathend000#. As principais vantagens destes filtros é que são estáveis e causais. São estáveis se todos os valores da resposta impulsiva g(t)
mathend000# são < 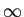 mathend000# e causais se g(t) = 0
mathend000# para t < 0
mathend000#. Temos portanto três casos possíveis segundo a forma do filtro G(f )
mathend000#:
mathend000# e causais se g(t) = 0
mathend000# para t < 0
mathend000#. Temos portanto três casos possíveis segundo a forma do filtro G(f )
mathend000#:
- a)
- se G(f )
mathend000# tem uma forma cuja TF inversa se pode calcular analiticamente com um número finito de amostras, então obtém-se a forma discreta g[k]
mathend000# de g(t)
mathend000# e efectua-se a filtragem por convolução discreta com o sinal de entrada utilizando (2-3.41).
- b)
- se a forma de G(f )
mathend000# não é tratável analiticamente, então temos de recorrer à amostragem em frequência para discretizar
G(f )
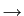 G[n]
mathend000# e poder aplicar uma TF discreta inversa (i.e. a versão discreta em frequência de (3-3.7)) para obter a forma de g[k]
mathend000# com um número finito de amostras que será, nesse caso, igual ao comprimento da TF discreta (número de amostras no intervalo
[- 1/2T, 1/2T]
mathend000#). Uma vez que obtivemos g[k]
mathend000# de duração L
mathend000# a filtragem faz-se, como anteriormente, por convolução com o sinal de entrada. O problema põe-se ao nível da qualidade da aproximação de G(f )
mathend000# por G[n]
mathend000#. Pode-se demonstrar que se obtém uma relação de aproximação entre G(n)
mathend000# e G(f )
mathend000# do tipo
G[n]
mathend000# e poder aplicar uma TF discreta inversa (i.e. a versão discreta em frequência de (3-3.7)) para obter a forma de g[k]
mathend000# com um número finito de amostras que será, nesse caso, igual ao comprimento da TF discreta (número de amostras no intervalo
[- 1/2T, 1/2T]
mathend000#). Uma vez que obtivemos g[k]
mathend000# de duração L
mathend000# a filtragem faz-se, como anteriormente, por convolução com o sinal de entrada. O problema põe-se ao nível da qualidade da aproximação de G(f )
mathend000# por G[n]
mathend000#. Pode-se demonstrar que se obtém uma relação de aproximação entre G(n)
mathend000# e G(f )
mathend000# do tipo
G(f )= 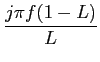 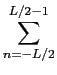 G(n) G(n)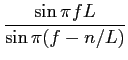 e-j e-j n/L, n/L,
|
(5-6.01) |
mathend000#
demonstrando-se então que a função de interpolação dá um erro de aproximação nulo às frequências n/L
mathend000# e finito entre essas frequências.
- c)
- por último, temos o caso no qual a equação que define G(f )
mathend000# é matemáticamente tratável mas a resposta impulsiva necessita um número infinito de amostras. Este é o caso mais comum quando a forma de G(f )
mathend000# é a de um dos filtros ideais. Já vimos que neste caso a limitação da duração de g(t)
mathend000# corresponde ao problema da limitação da duração de um sinal ilimitado. Aplica-se então toda a teoria das funções de observação (ou janelas) de diversos tipos segundo a forma de g(t)
mathend000# e o G(f )
mathend000# desejado. Vamos supôr que o filtro desejado é um passa baixo ideal é Gi(f )
mathend000# dado por
Gi(f )= 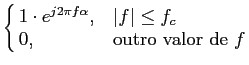
|
(5-6.02) |
mathend000#
onde fc
mathend000# é a freqência de corte e 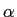 mathend000# é uma constante de fase, o que implica que o filtro é de fase linear. A resposta impulsiva do filtro ideal escreve-se como a TFI em tempo discreto de Gi(f )
mathend000#,
mathend000# é uma constante de fase, o que implica que o filtro é de fase linear. A resposta impulsiva do filtro ideal escreve-se como a TFI em tempo discreto de Gi(f )
mathend000#,
| gi[n] |
= |
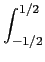 Gi(f )ej2 Gi(f )ej2 fndf fndf |
|
| |
= |
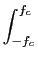 1 . e-j2 1 . e-j2 f f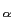 ej2 ej2 fndf fndf |
|
| |
= |
![$\displaystyle {{\sin[2\pi f_c(n-\alpha)]}\over {\pi (n-\alpha)}}$](img505.png) . . |
(5-6.03) |
Na prática, para obter um filtro FIR a partir da resposta impulsiva gi[n]
mathend000# esta tem que ser limitada no tempo, i.e., vamos ter que trabalhar com uma resposta impulsiva real, tal que
|
g[n] = gi[n]w[n],
|
(5-6.04) |
mathend000#
onde w[n]
mathend000# é chamada a função ou janela de observação. Como uma multiplicação no domínio do tempo corresponde a uma convolução no domínio da frequência podemos escrever (5-6.4)
| G(f ) |
= |
Gi(f ) 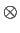 W(f ) W(f ) |
|
| |
= |
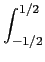 W( W(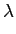 )Gi(f - )Gi(f - 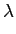 )d )d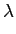 , , |
(5-6.05) |
onde o símbolo 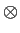 mathend000# significa convolução circular dado que, como já vimos, Gi(f )
mathend000# é uma função periódica a convolução também terá que ser periódica, ou seja, efectua-se no intervalo principal
[- 1/2, 1/2]
mathend000# e depois repete-se nos intervalos [1/2, 3/2]
mathend000#, [3/2, 5/2]
mathend000#, etc... Torna-se fácil avaliar analiticamente esta expressão de convolução porque Gi(f )
mathend000# é um filtro ideal. Algumas observações de ordem geral:
mathend000# significa convolução circular dado que, como já vimos, Gi(f )
mathend000# é uma função periódica a convolução também terá que ser periódica, ou seja, efectua-se no intervalo principal
[- 1/2, 1/2]
mathend000# e depois repete-se nos intervalos [1/2, 3/2]
mathend000#, [3/2, 5/2]
mathend000#, etc... Torna-se fácil avaliar analiticamente esta expressão de convolução porque Gi(f )
mathend000# é um filtro ideal. Algumas observações de ordem geral:
- por definição W(f )
mathend000# é a TF de uma função discreta limitada a L
mathend000# amostras e por isso terá um pico principal cuja largura é proporcional a 1/L
mathend000# e picos laterais de menor amplitude (tipo sin x/x
mathend000#),
- a convolução periódica (5-6.5) tem como efeito produzir uma versão desfocada de Gi(f )
mathend000#,
- o pico principal de W(f )
mathend000# tem como efeito criar uma banda de transição em Gi(f )
mathend000#, cuja largura vai depender da largura do pico principal, i.e., quanto menor for L
mathend000# maior será a largura do pico principal (proporcional a 1/L
mathend000#) e maior será também a banda de transição do filtro G(f )
mathend000# resultante,
- os picos laterais de W(f )
mathend000# resultam em oscilações equivalentes na banda passante e na banda de corte, que serão tanto maiores quanto maiores forem os picos laterais (em relação ao pico principal),
ao limite poderemos dizer que se L
mathend000# tendesse para infinito, W(f )
mathend000# tenderia para um dirac na frequência e teríamos
G(f )= Gi(f )
mathend000#. Passaremos em revista mais abaixo algumas das funções de observação mais utilizadas.
Na grande maioria dos casos as características definidas para um certo filtro dizem sómente respeito ao espectro de amplitude
|G(f )|
mathend000#. Assim a síntese do filtro faz-se livremente no que diz respeito à fase e, como é evidente, tenta-se sempre que a distorção de fase seja a menor possível, ou por outras palavras, tenta-se que o filtro tenha uma característica de fase linear
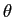 (f )= t0f
mathend000#. Para isso o filtro deve obedecer a uma condição do tipo
(f )= t0f
mathend000#. Para isso o filtro deve obedecer a uma condição do tipo
Gl(f )= G(f )e-j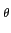 (f), (f),
|
(5-6.06) |
mathend000#
onde G(f )
mathend000# deve ter uma característica de fase nula 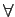 f
mathend000#. Para que a característica de fase seja nula é necessário e suficiente que a parte imaginária de G(f )
mathend000# seja ela mesma nula. Ora isto só é possível se g(t)
mathend000# for uma função par ou seja se
f
mathend000#. Para que a característica de fase seja nula é necessário e suficiente que a parte imaginária de G(f )
mathend000# seja ela mesma nula. Ora isto só é possível se g(t)
mathend000# for uma função par ou seja se
g(t) = g(- t), para |t|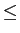 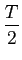 . .
|
(5-6.07) |
mathend000#
Como o filtro que obedece a (5-6.7) não é causal, porque tem metade da sua resposta impulsiva para t < 0
mathend000#, então temos de o deslocar de T/2
mathend000# no sentido de t > 0
mathend000#. Assim como um atraso temporal se transforma numa diferença de fase em frequência, obtem-se que
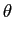 (f )= 2 (f )= 2 fT/2, fT/2,
|
(5-6.08) |
mathend000#
que é uma equação linear em f
mathend000#. Tal condição permite não só obter um sistema que não introduz distorção de fase mas também, tendo em conta a simetria (5-6.7), economizar metada das operações quando da convolução de g(t)
mathend000# com o sinal de entrada - ou mais precisamente da sua forma discreta g[k]
mathend000#.
Não falaremos aqui do último tipo de implementação possível de um filtro FIR que é a implementação recursiva através de uma equação do tipo (2-3.41) pois isto será discutido no próximo capítulo quando da discussão da síntese dos filtros IIR.
Para o caso de uma janela rectangular que permita obter um filtro estável e causal teríamos um função de observação
w[n] = 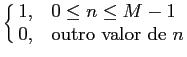
|
(5-6.09) |
mathend000#
cuja resposta em frequência é
W(f )= 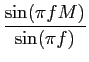 e-j e-j f(M-1), f(M-1),
|
(5-6.10) |
mathend000#
onde o termo de fase é devido ao facto de termos uma janela causal. Obviamente trata-se de uma função sinc em frequência. Neste caso a convolução circular expressa em (5-6.5) escreve-se
G(f )= 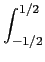 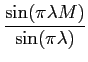 e-j e-j 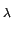 (M-1)Gi(f - (M-1)Gi(f - 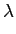 )d )d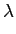 . .
|
(5-6.11) |
mathend000#
Se o filtro ideal Gi(f )
mathend000# for, por exemplo, do tipo passa baixo na banda
[- fc, fc]
mathend000# podemos reduzir o integral (5-6.11), considerando apenas a amplitude3, a
tal que
f + fc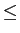 1/2
mathend000#, o que implica
-1/2 + fc
1/2
mathend000#, o que implica
-1/2 + fc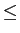 f
f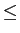 1/2 + fc
mathend000#. Assim (5-6.12) permite-nos obter um valor cumulativo da resposta em frequência independente do filtro desejado. A figura 5.10 mostra a função de observação rectangular no tempo (a), em amplitude na frequência (b), em dB também na frequência (c) e finalmente a resposta cumulativa na frequência (d) para um valor de M = 45
mathend000# amostras. Pode-se ver que:
1/2 + fc
mathend000#. Assim (5-6.12) permite-nos obter um valor cumulativo da resposta em frequência independente do filtro desejado. A figura 5.10 mostra a função de observação rectangular no tempo (a), em amplitude na frequência (b), em dB também na frequência (c) e finalmente a resposta cumulativa na frequência (d) para um valor de M = 45
mathend000# amostras. Pode-se ver que:
Figura 5.10:
janela de observação rectangular: no tempo (a), resposta em amplitude na frequência (b) resposta em dB (c) e cumulativa em dB (d), para M = 45
mathend000#
|
![\includegraphics[height=70mm,width=100mm]{figs/ampresrc.eps}](img511.png) |
- a resposta de amplitude em frequência tem o seu primeiro zero para f = 1/M
mathend000# e portanto a largura da banda de transição é aproximadamente o dobro, i.e.,
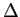 f = 2/M
mathend000#;
f = 2/M
mathend000#;
- o primeiro pico lateral encontra-se aproximadamente a f = 3/2M
mathend000# e por isso, substituindo na amplitude de (5-6.10), obtem-se o valor da atenuação nesse ponto que é de aproximadamente 2M/3
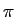 mathend000#. Dividindo este valor pelo valor do máximo, que é igual a M
mathend000#, obtem-se a atenuação entre o máximo e o primeiro pico lateral que vem a ser
2/3
mathend000#. Dividindo este valor pelo valor do máximo, que é igual a M
mathend000#, obtem-se a atenuação entre o máximo e o primeiro pico lateral que vem a ser
2/3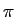
 0.2122 = 13
mathend000# db, e que se pode ver na figura 5.10(c), e finalmente
0.2122 = 13
mathend000# db, e que se pode ver na figura 5.10(c), e finalmente
- na figura 5.10(d) pode-se ver que a atenuação entre a banda passante e a banda de atenuação é de cerca de 21 dB.
Sendo a função rectangular a janela de observação mais simples e natural, como filtro ela contém algumas características indesejáveis / insuficientes no que diz respeito à implementação de filtros. Em particular no que diz respeito à atenuação na banda passante que é de apenas 21 dB, insuficiente em muitas aplicações. Além da função de observação rectangular existem outras funções de observação que permitem obter melhores resultados. Nos capítulos seguintes passamos em revista as funções de observação mais usuais e resumimos no quadro 1 as suas principais características. Podemos notar que, em geral, um aumento da atenuação na banda de corte encontra-se acompanhada de um aumento da banda de transição o que, na prática, torna a escolha da função de observação um compromisso entre estes dois factores. Esta lista de funções de observação não é exaustiva. O Matlab contém uma série destas funções pré-programadas.
Tabela 1:
tabela comparativa de janelas de observação temporais: principais características.
|
| Nome |
Banda de transição |
atenuação na |
| |
(
×fs
mathend000# Hz) |
banda de corte (db) |
| Rectangular |
0.9/M
mathend000# |
21 |
| Bartlett |
3.05/M
mathend000# |
25 |
| Hanning |
3.1/M
mathend000# |
44 |
| Hamming |
3.3/M
mathend000# |
53 |
| Blackman |
5.5/M
mathend000# |
74 |
|
Esta função resulta da convolução de duas funções rectangulares e permite obter uma transição mais suave de 0 para 1 do que a função rectangular. A função de Bartlett escreve-se
w[n] = 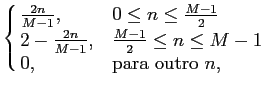
|
(5-6.13) |
mathend000#
A figura 5.11 mostra a função de observação de Bartlett no tempo (a), em amplitude na frequência (b), em dB também na frequência (c) e finalmente a resposta cumulativa na frequência (d) para um valor de M = 45
mathend000# amostras.
Figura 5.11:
janela de observação de Bartlett: no tempo (a), resposta em amplitude na frequência (b) resposta em dB (c) e cumulativa em dB (d), para M = 45
mathend000#.
|
![\includegraphics[height=70mm,width=100mm]{figs/ampresbr.eps}](img513.png) |
Neste caso a função de observação no tempo escreve-se
w[n] = ![$\displaystyle \cases{ 0.5[1-\cos({{2\pi n}\over {M-1}})], & $0 \le n \le M-1$\cr
0, & para outro $n$,\cr}
$](img514.png)
|
(5-6.14) |
mathend000#
A figura 5.12 mostra a função de observação de Hanning no tempo (a), em amplitude na frequência (b), em dB também na frequência (c) e finalmente a resposta cumulativa na frequência (d) para um valor de M = 45
mathend000# amostras.
Figura 5.12:
janela de observação de Hanning: no tempo (a), resposta em amplitude na frequência (b) resposta em dB (c) e cumulativa em dB (d), para M = 45
mathend000#.
|
![\includegraphics[height=70mm,width=100mm]{figs/ampreshn.eps}](img515.png) |
Neste caso a função de observação no tempo escreve-se
w[n] = ![$\displaystyle \cases{ 0.54-0.46\cos({{2\pi n}\over {M-1}})], & $0 \le n \le M-1$\cr
0, & para outro $n$,\cr}
$](img516.png)
|
(5-6.15) |
mathend000#
A figura 5.13 mostra a função de observação de Hamming no tempo (a), em amplitude na frequência (b), em dB também na frequência (c) e finalmente a resposta cumulativa na frequência (d) para um valor de M = 45
mathend000# amostras.
Figura 5.13:
janela de observação de Hamming: no tempo (a), resposta em amplitude na frequência (b) resposta em dB (c) e cumulativa em dB (d), para M = 45
mathend000#.
|
![\includegraphics[height=70mm,width=100mm]{figs/ampreshm.eps}](img517.png) |
Neste caso a função de observação no tempo escreve-se
w[n] = ![$\displaystyle \cases{ 0.42-0.5\cos({{2\pi n}\over {M-1}})] + 0.08\cos({{4\pi n}\over {M-1}}), & $0 \le n \le M-1$\cr
0, & para outro $n$,\cr}
$](img518.png)
|
(5-6.16) |
mathend000#
A figura 5.14 mostra a função de observação de Blackman no tempo (a), em amplitude na frequência (b), em dB também na frequência (c) e finalmente a resposta cumulativa na frequência (d) para um valor de M = 45
mathend000# amostras.
Figura 5.14:
janela de observação de Blackman: no tempo (a), resposta em amplitude na frequência (b) resposta em dB (c) e cumulativa em dB (d), para M = 45
mathend000#.
|
![\includegraphics[height=70mm,width=100mm]{figs/ampresbl.eps}](img519.png) |
A síntese de filtros IIR retira a sua metodologia dos métodos clássicos de síntese de filtros analógicos com a adequada transposição para o caso discreto. A implementação dos filtros IIR utiliza a equação de diferenças (2-3.41). Para que o filtro seja realizável é necessário, mais uma vez, que ele seja causal e estável, ou seja, que
e que
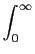 |g(t)|dt < |g(t)|dt < 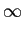 . .
|
(5-7.02) |
mathend000#
A função de transferência G(f )
mathend000# possui M
mathend000# pólos e N
mathend000# zeros que são respectivamente os zeros do denominador e do numerador. Para que o filtro seja estável é necessário que os pólos de G(f )
mathend000# estejam no interior do círculo unidade.
A metodologia a aplicar na síntese de filtros IIR reside na transposição dos filtros analógicos para filtros digitais. Nessa transformação é necessário que o eixo imaginário do plano j mathend000# passe para o círculo unidade do plano
exp(j
mathend000# passe para o círculo unidade do plano
exp(j T)
mathend000# e que o meio-plano esquerdo do plano j
T)
mathend000# e que o meio-plano esquerdo do plano j mathend000# passe para o interno do círculo unidade do plano
exp(j
mathend000# passe para o interno do círculo unidade do plano
exp(j T)
mathend000#. Estas duas condições garantem que um filtro analógico estável se traduza por um filtro digital estável. Os filtros analógicos mais conhecidos são os filtros de Butterworth (5.7.1), os filtros de Chebyshev (5.7.2) e os filtros elípticos (5.7.3). Por outro lado a passagem de uma função contínua de
T)
mathend000#. Estas duas condições garantem que um filtro analógico estável se traduza por um filtro digital estável. Os filtros analógicos mais conhecidos são os filtros de Butterworth (5.7.1), os filtros de Chebyshev (5.7.2) e os filtros elípticos (5.7.3). Por outro lado a passagem de uma função contínua de  mathend000# para uma função discreta fará intervir um processo de amostragem que só será tratado no programa de Processamento Digital de Sinal.
mathend000# para uma função discreta fará intervir um processo de amostragem que só será tratado no programa de Processamento Digital de Sinal.
Filtros Butterworth
Os filtros de Butterworth são especificados de modo a terem uma função de transferência com o mínimo de oscilações tanto na banda passante como na banda de corte. O módulo quadrado da resposta em frequência do filtro que obedece a esta especificação escreve-se
onde N
mathend000# é a ordem do filtro e 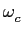 mathend000# é a frequência de corte passa-baixo equivalente. De notar que a partir de (5-7.3) temos que
|H(
mathend000# é a frequência de corte passa-baixo equivalente. De notar que a partir de (5-7.3) temos que
|H(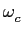 )|= 1/
)|= 1/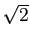 mathend000# e
|H(0)|= 1
mathend000#. Além disso, a inclinação de
|H(
mathend000# e
|H(0)|= 1
mathend000#. Além disso, a inclinação de
|H( )|
mathend000# para
)|
mathend000# para
 >
> 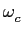 mathend000# é proporcional a
(1/
mathend000# é proporcional a
(1/ )N
mathend000#. A figura 5.15 mostra o módulo das respostas em frequência dos filtros de Butterworth numa escala linear e para valores de N = 3
mathend000# e N = 4
mathend000#.
)N
mathend000#. A figura 5.15 mostra o módulo das respostas em frequência dos filtros de Butterworth numa escala linear e para valores de N = 3
mathend000# e N = 4
mathend000#.
Figura 5.15:
resposta em frequência filtros Butterworth para N = 3
mathend000# e N = 4
mathend000#.
|
![\includegraphics[height=70mm,width=100mm]{figs/butterworth.ps}](img522.png) |
Filtros Chebyshev
No caso dos filtros de Chebyshev, pode-se obter uma maior inclinação entre a banda passante e a banda de corte, autorizando uma banda de transição mais estreita, tendo de ``pagar'' por isso uma maior oscilação da resposta em frequência na banda passante ou de corte. Os filtros de Chebyshev podem ser de dois tipos: tipo I - com oscilações só na banda passante ou tipo II - só com oscilações na banda de corte, conforme exemplificado na figura 5.16.
Figura 5.16:
resposta em frequência dos filtros Chebyshev tipo I e II
|
![\includegraphics[height=70mm,width=100mm]{figs/chebyshev.ps}](img523.png) |
O módulo ao quadrado da resposta em frequência é, neste caso, dada por
|G(fa)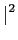 = = 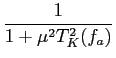 , , 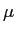 real < 1 real < 1
|
(5-7.04) |
mathend000#
onde TK(fa)
mathend000# é o polinómio de Chebyshev de ordem K
mathend000# para a frequência normalizada fa = f /fc
mathend000#, dado por
TK(fa) = 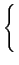 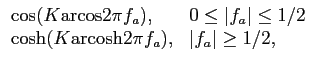
|
(5-7.05) |
mathend000#
e que se pode calcular recursivamente,
|
TK+1(x) = 2xTK(x) - TK-1(x),
|
(5-7.06) |
mathend000#
com T0(x) = 1
mathend000# e T1(x) = x
mathend000#. Como TN(1) = 1
mathend000# para todo os valores de N
mathend000#, temos que o módulo ao quadrado para f = fc
mathend000# é igual a
![]() (f )
(f )
![]() ) = H0X(
) = H0X(![]() )exp(- j
)exp(- j![]() t0),
t0),
![]() (t - t0).
(t - t0).
![]() )|
)|
![]() >
> ![]()
![]() )
)
![]()
![]()
![]() = 0
= 0
![]()
![]() ) =
) = ![]() .
.
![]()
![]() )
)
![]() )|=
)|= 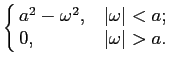
![]() =
= 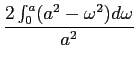 =
= ![]() a,
a,
![]() =
= ![]() a
a
![]()
![]() .
.
![]()
![]() |H(
|H(![]() )|e-j
)|e-j![]() (
(![]() )ej
)ej![]() td
td![]() ,
,
![]()
![]() |H(
|H(![]() )|cos[
)|cos[![]() t -
t - ![]() (
(![]() )]d
)]d![]() .
.
![]() t -
t - ![]() (
(![]() )] = 1
)] = 1
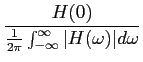 =
= ![]() ,
,
![]() h(
h(![]() )u(t -
)u(t - ![]() )d
)d![]() ,
,
![]()
![]()
![]() = 0
= 0
![]() ) = H(
) = H(![]() )U(
)U(![]() ) =
) = ![]() H(
H(![]() )
)![]() (
(![]() ) +
) + 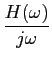 ,
,
![]()
![]() H(
H(![]() )
)![]() (
(![]() )ej
)ej![]() td
td![]() +
+ ![]()
![]()
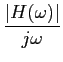 ej[
ej[![]() (t-t0)]d
(t-t0)]d![]() .
.
![]() ) = H * (
) = H * (![]() )
)
![]()
![]()
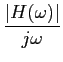 ej[
ej[![]() (t-t0)]d
(t-t0)]d![]()
![]()
![]()
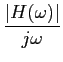 cos[
cos[![]() (t - t0)]d
(t - t0)]d![]() +
+![]()
![]()
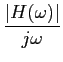 sin[
sin[![]() (t - t0)]d
(t - t0)]d![]()
![]()
![]() ,
,![]() ]
]
![]() )
)
![]() h(
h(![]() )d
)d![]() +
+ ![]() h(
h(![]() )d
)d![]() ,
,
![]() )
)
![]() h(
h(![]() )d
)d![]() =
= 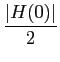 =
= 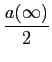 .
.
![]()
![]() =
= 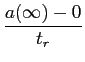 = hmax = h(t0),
= hmax = h(t0),
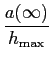 =
= ![]() = Dt =
= Dt = ![]() ,
,
![]() )|=
)|= ![]()
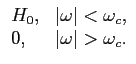
![]() (
(![]() ) = t0
) = t0![]()
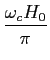
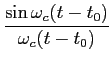 ,
,
![]() =
= ![]() (t - t0)
(t - t0)
![]() +
+ ![]()
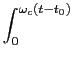
![]() d
d![]() .
.
![]() ) = 0, |
) = 0, |![]() |>
|> ![]()
![]() )
)
![]() ) = H(
) = H(![]() )X(
)X(![]() ) = X(
) = X(![]() )H0e-j
)H0e-j![]() t0,
t0,
![]() (
(![]() ) =
) = ![]() t0
t0
![]()
![]()
![]() (
(![]() ) =
) = ![]() (
(![]() ) +
) + ![]()
![]() (
(![]() ),
),
![]() ) =|H(
) =|H(![]() )|e-j
)|e-j![]() (
(![]() ) =|H(
) =|H(![]() )|e-j[
)|e-j[![]() (
(![]() )+
)+![]()
![]() (
(![]() )],
)],
![]() ) = H0(
) = H0(![]() )e-j
)e-j![]()
![]() (
(![]() ),
),
![]() )
)
![]()
![]() (
(![]() )
) ![]() 1
1
![]()
![]() (
(![]() )
) ![]() 1 - j
1 - j![]()
![]() (
(![]() ),
),
![]() )
) ![]() H0(
H0(![]() )[1 - j
)[1 - j![]()
![]() (
(![]() )].
)].
![]()
![]() (
(![]() ) = b sin
) = b sin![]()
![]()
![]() ,
,
![]() )
) ![]() H0(
H0(![]() )[1 -
)[1 - ![]() ejn
ejn![]()
![]() /
/![]() +
+ ![]() e-jn
e-jn![]()
![]() /
/![]() ],
],
![]() h0(t) -
h0(t) - ![]() h0(t +
h0(t + ![]() ) +
) + ![]() h0(t -
h0(t - ![]() ),
),
![]() ,
,![]() )
)
![]()
![]() (
(![]() ) =
) = ![]() Bnsin(
Bnsin(![]() ),
),
![]()
![]()
![]()
![]() (
(![]() )sin(
)sin(![]() )d
)d![]() ,
,
![]() ) = H0(
) = H0(![]() )[J0(b) + J1(b)e
)[J0(b) + J1(b)e![]() + J-1(b)e
+ J-1(b)e![]() + ...],
+ ...],
![]() /
/![]()
![]() ) =
) = 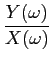 = A(
= A(![]() )ej
)ej![]() (
(![]() ),
),
![]() )|= f (log10
)|= f (log10![]() )
)
![]() (
(![]() ) = g(log10
) = g(log10![]() ).
).
![]() )
)
![]() )
)![]() )ej
)ej![]() (
(![]() )
)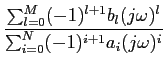
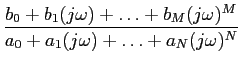 ,
,![]() ) = K
) = K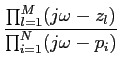 ,
,
![]() - zi)l
- zi)l
![]() 0
0
![]() )l
)l
![]()
![]()
![]() )l
)l
![]() )l
)l
![]() T
T
![]() T)
T)
![]() )
)![]()
![]()
![]()
![]() 0 log10
0 log10![]() T
T![]() )
)![]()
![]()
![]()
![]() 20 log10
20 log10![]() T
T![]() <
< ![]()
![]() >
> ![]()
![]() = 1/T
= 1/T
![]() =
= ![]()
![]() /10
/10
![]()
![]() )
)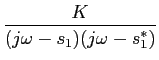
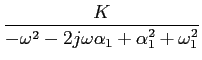 ,
,![]() + j
+ j![]()
![]() = -
= - ![]() /
/![]()
![]() =
= ![]() +
+ ![]()
![]()
![]()
![]()
![]()
![]() = 0
= 0
![]()
![]() =
= ![]()
![]() > 1
> 1
![]() < 1
< 1
![]() )|
)|
![]()
![]()
![]() < 1/
< 1/![]()
![]() < 0.707
< 0.707
![]() < 1
< 1
![]() < 0.707
< 0.707
![]()
![]() )|= AM =
)|= AM = 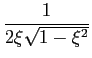 .
.
![]()
![]()
![]()
![]()
![]()
![]() = 0
= 0
![]()
![]() /
/![]()
![\includegraphics[height=90mm,width=120mm]{figs/order_2.eps}](img475.png)
![]() (
(![]() )
)![]() {
{![]() -
- ![]() +2j
+2j![]()
![]()
![]() }
}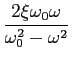 ,
,![]()
![]()
![]()
![]()
![]()
![]()
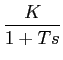 ,
,
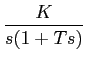 ,
,
![]() 3T
3T
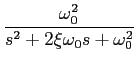 ,
,
![]()
![]() ±j
±j![]()
 .
.
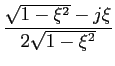 ,
,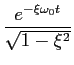 [
[![]() sin(
sin(![]() t
t ) +
) +  cos(
cos(![]() t
t )].
)].
![]() = cos
= cos![]()
![]() = sin
= sin![]()
![]()
![\includegraphics[height=60mm,width=100mm]{figs/ordem_2_t.eps}](img492.png)
![]() =
= ![]()
![]()
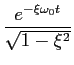 sin(
sin(![]() t
t +
+ ![]() ) -
) - 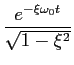 cos(
cos(![]() t
t +
+ ![]() )
)![]()
 = 0,
= 0,
![]() sin(
sin(![]() t
t +
+ ![]() ) = cos(
) = cos(![]() t
t +
+ ![]() )
) ,
,
![]()
![]()
 tp +
tp + ![]() ) = tan
) = tan![]() ,
,
![]()
 tp = k
tp = k![]() ,
,
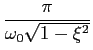 ,
,
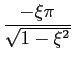 ).
).
![]()
![]()
![\includegraphics[height=60mm,width=100mm]{figs/ap_ordem2.eps}](img495.png)
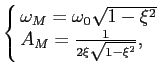
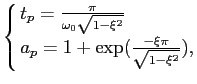
![]()
![]() = 0.425
= 0.425
![]()
![]() G[n]
G[n]
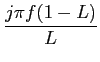
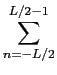 G(n)
G(n)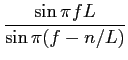 e-j
e-j![]() n/L,
n/L,
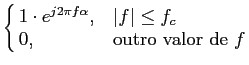
![]()
![]()
![]() (f )= t0f
(f )= t0f
![]() (f),
(f),
![]() f
f
![]() (f )= 2
(f )= 2![]() fT/2,
fT/2,
![]() 1/2
1/2
![]() f
f![]() 1/2 + fc
1/2 + fc
![\includegraphics[height=70mm,width=100mm]{figs/ampresrc.eps}](img511.png)
![]() f = 2/M
f = 2/M
![]()
![]()
![]() 0.2122 = 13
0.2122 = 13
![\includegraphics[height=70mm,width=100mm]{figs/ampresbr.eps}](img513.png)
![\includegraphics[height=70mm,width=100mm]{figs/ampreshn.eps}](img515.png)
![\includegraphics[height=70mm,width=100mm]{figs/ampreshm.eps}](img517.png)
![\includegraphics[height=70mm,width=100mm]{figs/ampresbl.eps}](img519.png)
![]() |g(t)|dt <
|g(t)|dt < ![]() .
.
![]()
![]() T)
T)
![]()
![]() T)
T)
![]()
![]()
![]() )|= 1/
)|= 1/![]()
![]() )|
)|
![]() >
> ![]()
![]() )N
)N
![]() =
= 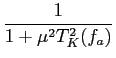 ,
, ![]() real < 1
real < 1
![]()
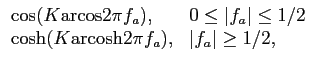
![\includegraphics[height=50mm]{figs/dist-amplitude.eps}](img399.png)
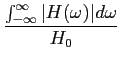 ,
,
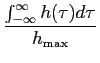 =
= 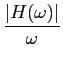 sin[
sin[![\includegraphics[height=60mm,width=90mm]{figs/impulsiva-indicial.eps}](img423.png)
![\includegraphics[height=50mm]{figs/filtro-pb-ideal.eps}](img427.png)
![\includegraphics[height=90mm,width=120mm]{figs/ordem-0.eps}](img456.png)
![\includegraphics[height=90mm,width=120mm]{figs/ordem-1.eps}](img461.png)
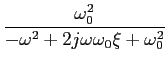 ,
,
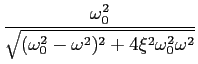 .
.
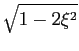 ,
,
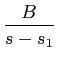 +
+ 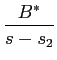
![\includegraphics[width=100mm]{figs/gabarito-filtros.eps}](img498.png)
![$\displaystyle {{\sin[2\pi f_c(n-\alpha)]}\over {\pi (n-\alpha)}}$](img505.png) .
.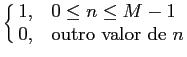
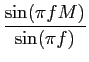 e-j
e-j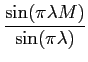 e-j
e-j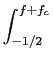
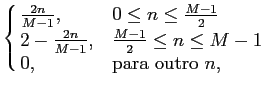
![$\displaystyle \cases{ 0.5[1-\cos({{2\pi n}\over {M-1}})], & $0 \le n \le M-1$\cr
0, & para outro $n$,\cr}
$](img514.png)
![$\displaystyle \cases{ 0.54-0.46\cos({{2\pi n}\over {M-1}})], & $0 \le n \le M-1$\cr
0, & para outro $n$,\cr}
$](img516.png)
![$\displaystyle \cases{ 0.42-0.5\cos({{2\pi n}\over {M-1}})] + 0.08\cos({{4\pi n}\over {M-1}}), & $0 \le n \le M-1$\cr
0, & para outro $n$,\cr}
$](img518.png)
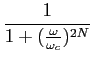 ,
,
![\includegraphics[height=70mm,width=100mm]{figs/butterworth.ps}](img522.png)
![\includegraphics[height=70mm,width=100mm]{figs/chebyshev.ps}](img523.png)