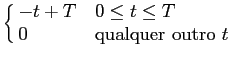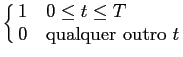mathend000#.
a) calcule a resposta impulsiva h(t)
mathend000#. Trata-se de um sistema causal ?
Justifique a sua resposta.
b) multiplicando h(t)
mathend000# por uma função
p(t) = rect(t - t0)
mathend000#,
determine o sinal resultante y(t)
mathend000#.
c) y(t)
mathend000# é causal ? Justifique a sua resposta.
d) calcule Y(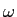 )
mathend000#. Faça um esboço de
|Y(
)
mathend000#. Faça um esboço de
|Y(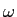 )|
mathend000# e
compare com a resposta em frequência do filtro passa-baixo H(
)|
mathend000# e
compare com a resposta em frequência do filtro passa-baixo H(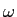 )
mathend000#
inicial.
)
mathend000#
inicial.
Problema 2: considere o sinal y(t)
mathend000# dado por
y(t) = s(t) + n(t)
mathend000#
onde s(t)
mathend000# é um sinal determinístico e n(t)
mathend000# é
a) um ruído branco gaussiano, não correlacionado com s(t)
mathend000# e
de potência 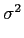 mathend000#. Explique cada um dos termos empregues nesta frase
relativamente ao sinal n(t)
mathend000#.
mathend000#. Explique cada um dos termos empregues nesta frase
relativamente ao sinal n(t)
mathend000#.
b) calcule E[y(t)]
mathend000#
c) calcule V[y(t)]
mathend000#
Exame de Sistemas e Sinais - Janeiro 2003
Problema 1: a resposta impulsiva de um filtro RC é dada por
h(
t) =
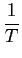 e-t/Tu
e-t/Tu(
t)
mathend000#
onde T
mathend000# é uma constante real e positiva e u(t)
mathend000# é a função
degrau unidade.
a) calcule a função de autocorrelação rh(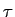 )
mathend000# de h(t)
mathend000#.
)
mathend000# de h(t)
mathend000#.
b) faça um esboço da função de autocorrelação rh(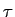 )
mathend000#.
)
mathend000#.
c) qual a energia total contida no sinal h(t)
mathend000# ? Justifique a sua resposta.
d) calcule a densidade espectral de potência
Ph(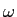 )
mathend000#.
)
mathend000#.
e) faça o esboço do diagrama de Bode de
Ph(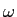 )
mathend000# (amplitude e
fase). Qual a ordem do sistema ? Justifique a sua resposta.
)
mathend000# (amplitude e
fase). Qual a ordem do sistema ? Justifique a sua resposta.
f) calcule a banda passante a -3 dB do sistema a partir da sua resposta em
frequência.
Problema 2: considere o seguinte sinal
m(
t) =
Ae-t2/2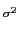
mathend000#
com
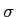 = 0.1
mathend000# ms e A
mathend000# uma constante real positiva.
= 0.1
mathend000# ms e A
mathend000# uma constante real positiva.
a) calcule e represente o espectro de amplitude M(f )
mathend000# de m(t)
mathend000#.
b) calcule a banda passante a -3 dB do espectro M(f )
mathend000#.
c) desejando enviar o sinal m(t)
mathend000# através de um canal de transmissão
analógico utilizando modulação de amplitude de banda lateral
única USSB, escrever a forma do sinal modulador a(t)
mathend000# e
demonstrar que o respectivo espectro só contém frequências positivas
ou nulas.
Exame de Sistemas e Sinais - Fevereiro 2003
Problema 1: considere o sinal periódico s(t)
mathend000# dado por
s(
t) =
A cos(
 t
t)
mathend000#
onde A
mathend000# é uma constante real positiva e a pulsação
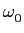 = 2
= 2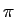 /T0
mathend000#.
/T0
mathend000#.
a) calcule o coeficiente Cn
mathend000# do desenvolvimento em série de s(t)
mathend000#.
b) calcule a Transformada de Fourier S(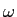 )
mathend000# de s(t)
mathend000#.
)
mathend000# de s(t)
mathend000#.
c) considere agora o seguinte sinal periódico (``trem de Diracs'')
a(
t) =
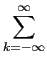
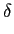
(
t -
kTs)
mathend000#
onde Ts
mathend000# é o período, com
Ts < T0/2
mathend000#. Calcule o seu desenvolvimento
em série complexa e a sua Transformada de Fourier A(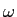 )
mathend000#.
)
mathend000#.
d) considere agora o sinal amostrado
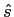 (t) = s(t)a(t)
mathend000#, resultado
da multiplicação de s(t)
mathend000# pelo trem de Diracs a(t)
mathend000#. Calcule o
espectro
(t) = s(t)a(t)
mathend000#, resultado
da multiplicação de s(t)
mathend000# pelo trem de Diracs a(t)
mathend000#. Calcule o
espectro
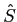 (
(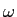 )
mathend000#.
)
mathend000#.
e) compare
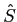 (
(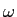 )
mathend000# com S(
)
mathend000# com S(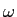 )
mathend000#. Faça um esboço de
)
mathend000#. Faça um esboço de
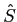 (
(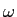 )
mathend000#. Quais as frequências presentes entre
[-
)
mathend000#. Quais as frequências presentes entre
[- 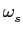 ,
,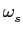 ]
mathend000# com
]
mathend000# com
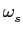 = 2
= 2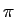 /Ts
mathend000# ? Conclusão.
/Ts
mathend000# ? Conclusão.
Problema 2: considere um sistema de resposta impulsiva
h(t) = exp(- at)u(t)
mathend000#
onde a
mathend000# é uma constante real positiva e u(t)
mathend000# é o degrau unidade.
a) utilizando a equação de convolução, calcule e faça o esboço
da resposta y(t)
mathend000# do sistema a um sinal de entrada
x(t) = rect[(t - T/2)/T]
mathend000#, onde T
mathend000# é uma constante real positiva.
b) calcule a Transformada de Fourier H(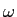 )
mathend000# do sistema h(t)
mathend000# e
represente o seu diagrama de Bode (módulo e fase).
)
mathend000# do sistema h(t)
mathend000# e
represente o seu diagrama de Bode (módulo e fase).
c) determine a banda passante a -3 dB do sistema.
d) calcule a Transformada de Fourier X(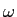 )
mathend000# do sinal de entrada x(t)
mathend000#
e faça o esboço do seu módulo.
)
mathend000# do sinal de entrada x(t)
mathend000#
e faça o esboço do seu módulo.
e) qual o valor mínimo da constante T
mathend000# que permite ter no sinal de
saída y(t)
mathend000# as componentes principais do sinal x(t)
mathend000# com uma
atenuação até 3 dB.
Exame de Sistemas e Sinais - Janeiro 2005
Problema 1: considere um sistema linear e invariante no tempo descrito pela sua resposta impulsiva discreta h(n)
mathend000#,
h(
n) = (0.9)
nu(
n)

(1.1)
mathend000#
onde u(n)
mathend000# é a função degrau unidade.
- a)
- trata-se de um sistema causal ? E estável ? Justifique as suas respostas.
- b)
- calcule a resposta y(n)
mathend000# do sistema a um sinal de entrada x(n)
mathend000# dado por
x(
n) =
u(
n) -
u(
n - 10)

(1.2)
mathend000#
- c)
- calcule a resposta em frequência H(f )
mathend000# do sistema
- d)
- calcule e faça os esboços do módulo e da fase de H(f )
mathend000# para
-1/2
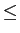 f
f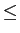 1/2
mathend000#.
1/2
mathend000#.
Problema 2: considere o sinal real x(t)
mathend000# definido por
x(
t) =
e-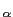 tu
tu(
t)

(2.1)
mathend000#
onde u(t)
mathend000# é a função degrau unidade e 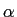 mathend000# é uma constante real positiva. Considere agora o sinal real y(t)
mathend000# dado por
mathend000# é uma constante real positiva. Considere agora o sinal real y(t)
mathend000# dado por
y(
t) =
x(
t -
t0) +
w(
t)

(2.2)
mathend000#
onde o atraso temporal t0 > 0
mathend000# e w(t)
mathend000# é uma sequencia de ruído aleatório branco e Gaussiano de média nula e de desvio padrão 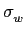 mathend000# .
mathend000# .
- a)
- calcule a função de correlação cruzada
rxy(
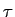 )
mathend000# entre x(t)
mathend000# e y(t)
mathend000#.
)
mathend000# entre x(t)
mathend000# e y(t)
mathend000#.
- b)
- faça um esboço de
rxy(
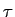 )
mathend000# e determine qual o instante tM1
mathend000# para o qual a função atinge o seu valor máximo e qual esse valor máximo vM1
mathend000#.
)
mathend000# e determine qual o instante tM1
mathend000# para o qual a função atinge o seu valor máximo e qual esse valor máximo vM1
mathend000#.
- c)
- calcule agora a autocorrelação
ryy(
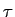 )
mathend000# de y(t)
mathend000#.
)
mathend000# de y(t)
mathend000#.
- d)
- faça um esboço de
ryy(
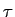 )
mathend000# e deduza quais os valores do instante do máximo e o seu valor tM2
mathend000# e vM2
mathend000#, respectivamente. Compare com os valores tM1
mathend000# e vM1
mathend000#, obtidos para a função de correlação cruzada rxy
mathend000#, e justifique o resultado.
)
mathend000# e deduza quais os valores do instante do máximo e o seu valor tM2
mathend000# e vM2
mathend000#, respectivamente. Compare com os valores tM1
mathend000# e vM1
mathend000#, obtidos para a função de correlação cruzada rxy
mathend000#, e justifique o resultado.
Exame de Sistemas e Sinais - Janeiro 2007
Problema 1 [8 val.]: considere o sistema descrito pela sua resposta impulsiva discreta h(n)
mathend000#
h(
n) =
u(
n) -
u(
n - 3)

(1.1)
mathend000#
onde u(n)
mathend000# é a função degrau unidade discreta.
- a)
- [1.5v] demonstre que o sistema descrito por h(n)
mathend000# é linear e invariante no tempo.
- b)
- [1.5v] determine se o sistema é causal e estável. Justifique.
- c)
- [1v] represente h(n)
mathend000#.
- d)
- [2.5v] calcule H(f )
mathend000# transformada de Fourier de h(n)
mathend000#.
- e)
- [1.5v] faça um esboço de H(f )
mathend000# em módulo e fase para
-1/2
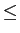 f
f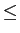 1/2
mathend000#.
1/2
mathend000#.
Problema 2 [7 val.]: considere o sinal s(t)
mathend000# descrito por (2.1) e a sua observação com ruído x(t)
mathend000# dada por (2.2),
mathend000#
x(
t) =
s(
t) +
w(
t)

(2.2)
mathend000#
onde A
mathend000#, 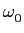 mathend000# e
mathend000# e 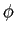 mathend000# são constantes de amplitude, pulsação e fase, respectivamente, e onde w(t)
mathend000# é uma sequência aleatória branca, de média nula, com variância
mathend000# são constantes de amplitude, pulsação e fase, respectivamente, e onde w(t)
mathend000# é uma sequência aleatória branca, de média nula, com variância
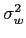 mathend000# e independente de s(t)
mathend000#.
mathend000# e independente de s(t)
mathend000#.
- a)
- [2v] calcule a função de autocorrelação rs(
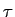 )
mathend000# de s(t)
mathend000#.
)
mathend000# de s(t)
mathend000#.
- b)
- [2v] calcule a função de autocorrelação rx(
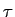 )
mathend000# de x(t)
mathend000#.
)
mathend000# de x(t)
mathend000#.
- c)
- [2v] calcule a densidade espectral de potência Px(f )
mathend000# de x(t)
mathend000#.
- d)
- [1v] faça um esboço de Px(f )
mathend000#.
Problema 3 [5 val.]: considere os dois sinais
s1(
t) =
u(
t) -
u(
t -
t0)

(3.1)
mathend000#
s2(
t) =
e-t/t0u(
t)

(3.2)
mathend000#
onde u(t)
mathend000# é a função degrau unidade e t0
mathend000# é uma constante positiva.
- a)
- [4v] calcule a função de correlação r(
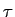 )
mathend000# entre s1(t)
mathend000# e s2(t)
mathend000#.
)
mathend000# entre s1(t)
mathend000# e s2(t)
mathend000#.
- b)
- [1v] faça um esboço de r(
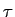 )
mathend000#.
)
mathend000#.
Exame de Sinais e Sistemas - Fevereiro 2007
Problema 1 [5 val]: considere um sistema descrito pela sua resposta impulsiva discreta h(n)
mathend000#,
h(
n) =
A sin(2
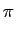 K0n
K0n +
k0)

(1.1)
mathend000#
onde A
mathend000#, K0
mathend000# e k0
mathend000# são constantes reais.
- a)
- [1v] trata-se de um sistema causal ? E estável ? Justifique as suas respostas.
- b)
- [2.5v] calcule a resposta em frequência H(f )
mathend000# do sistema
- c)
- [1.5v] calcule e faça os esboços do módulo e da fase de H(f )
mathend000# para
-1/2
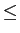 f
f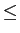 1/2
mathend000#.
1/2
mathend000#.
Problema 2 [4 val.]: um filtro Butterworth de fase linear é definido por
mathend000#
Calcule h(t)
mathend000# para n = 1
mathend000#.
Problema 3 [7 val.]: considere o sinal real x(t)
mathend000# definido por
x(
t) =
e-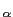 tu
tu(
t)

(3.1)
mathend000#
onde u(t)
mathend000# é a função degrau unidade e 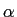 mathend000# é uma constante real positiva. Considere agora o sinal real y(t)
mathend000# dado por
mathend000# é uma constante real positiva. Considere agora o sinal real y(t)
mathend000# dado por
y(
t) =
x(
t -
t0) +
w(
t)

(3.2)
mathend000#
onde o atraso temporal t0 > 0
mathend000# e w(t)
mathend000# é uma sequência de ruído aleatório branco e Gaussiano de média nula e de desvio padrão 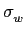 mathend000# .
mathend000# .
- a)
- [2v] calcule a função de correlação cruzada
rxy(
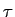 )
mathend000# entre x(t)
mathend000# e y(t)
mathend000#.
)
mathend000# entre x(t)
mathend000# e y(t)
mathend000#.
- b)
- [1v] faça um esboço de
rxy(
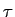 )
mathend000# e determine qual o instante tM1
mathend000# para o qual a função atinge o seu valor máximo e qual esse valor máximo vM1
mathend000#.
)
mathend000# e determine qual o instante tM1
mathend000# para o qual a função atinge o seu valor máximo e qual esse valor máximo vM1
mathend000#.
- c)
- [2v] calcule agora a autocorrelação
ryy(
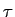 )
mathend000# de y(t)
mathend000#.
)
mathend000# de y(t)
mathend000#.
- d)
- [2v] faça um esboço de
ryy(
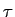 )
mathend000# e deduza quais os valores do instante do máximo e o seu valor tM2
mathend000# e vM2
mathend000#, respectivamente. Compare com os valores tM1
mathend000# e vM1
mathend000#, obtidos para a função de correlação cruzada rxy
mathend000#, e justifique o resultado.
)
mathend000# e deduza quais os valores do instante do máximo e o seu valor tM2
mathend000# e vM2
mathend000#, respectivamente. Compare com os valores tM1
mathend000# e vM1
mathend000#, obtidos para a função de correlação cruzada rxy
mathend000#, e justifique o resultado.
Problema 4: [4 val.] seja o sinal x(t)
mathend000# dado por
mathend000#
onde a
mathend000#, 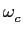 mathend000# e
mathend000# e 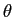 mathend000# são constantes.
mathend000# são constantes.
- a)
- [2v] calcule a função de autocorrelação de x(t)
mathend000#.
- b)
- [2v] calcule a densidade espectral de potência de x(t)
mathend000#.
Exame de Sinais e Sistemas - Fevereiro 2008
Exercício 1: considere o sinal discreto x[n]
mathend000# da equação (C-7.1)
onde a < 1
mathend000# e u(n)
mathend000# é a função degrau unidade.
- a)
- calcule e faça um esboço da função de autocorrelação rx[k]
mathend000# de x[n]
mathend000#
- b)
- calcule a TFDT X(
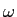 )
mathend000# do sinal x[n]
mathend000#
)
mathend000# do sinal x[n]
mathend000#
- c)
- calcule a densidade espectral de potência
Px(
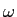 )
mathend000# do sinal x(t)
mathend000#.
)
mathend000# do sinal x(t)
mathend000#.
- d)
- faça um esboço de
Px(
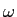 )
mathend000#.
)
mathend000#.
Exercício 2: considere a equação entrada - saída de um filtro IIR
|
y[n] = - y[n - 2] - 2y[n - 1] + x[n],
|
(C.-7.2) |
mathend000#
- a)
- qual a ordem deste filtro ? Quais os coeficientes a0
mathend000#, a1
mathend000#, a2
mathend000# e b0
mathend000# do filtro.
- b)
- demonstre que a função de transferência H(
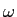 )
mathend000# deste filtro se escreve
)
mathend000# deste filtro se escreve
H(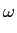 ) = ) = ![$\displaystyle {{e^{j\omega}}\over {2[1+\cos (\omega)]}}$](img570.png)
|
(C.-7.3) |
mathend000#
assumindo um período de amostragem unitário.
- c)
- trace um esboço do módulo e da fase de H(
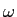 )
mathend000#
)
mathend000#
- d)
- diga como classifica este filtro: i) sem distorção, ii) com distorção de amplitude, iii) com distorção de fase ou iv) com distorção de amplitude e de fase. Justifique a sua resposta.
- e)
- de que tipo de filtro se trata: passa-baixo, passa-alto, passa-banda ou corta banda ? Justique.
Exercício 3: considere o sinal x(t)
mathend000# tal que
x(t) = 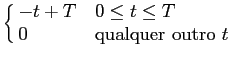
|
(C.-7.4) |
mathend000#
- a)
- represente o sinal x(t)
mathend000#
- b)
- represente a resposta impulsiva h(t)
mathend000# de um sistema linear invariante dada por
h(t) = 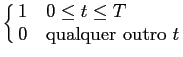
|
(C.-7.5) |
mathend000#
- c)
- determine graficamente a resposta y(t)
mathend000# ao sinal x(t)
mathend000#, tomando o cuidado de especificar os intervalos de definição para cada caso.
- d)
- calcule a expressão do sinal de saída y(t)
mathend000# determinado na alínea c)
Sergio Jesus
2008-12-30
![]() )
)
![]() )|
)|
![]() )
)
![]()
![]() e-t/Tu(t)
e-t/Tu(t)
![]() )
)
![]() )
)
![]() )
)
![]() )
)
![]()
![]() = 0.1
= 0.1
![]() t)
t)
![]() = 2
= 2![]() /T0
/T0
![]() )
)
![]()
![]() (t - kTs)
(t - kTs)
![]() )
)
![]() (t) = s(t)a(t)
(t) = s(t)a(t)
![]() (
(![]() )
)
![]() (
(![]() )
)
![]() )
)
![]() (
(![]() )
)
![]() ,
,![]() ]
]
![]() = 2
= 2![]() /Ts
/Ts
![]() )
)
![]() )
)
![]() (1.1)
(1.1)
![]() (1.2)
(1.2)
![]() f
f![]() 1/2
1/2
![]() tu(t)
tu(t)![]() (2.1)
(2.1)
![]()
![]() (2.2)
(2.2)
![]()
![]() )
)
![]() )
)
![]() )
)
![]() )
)
![]() (1.1)
(1.1)
![]() f
f![]() 1/2
1/2
![]() t +
t + ![]() )
)![]() (2.1)
(2.1)
![]() (2.2)
(2.2)
![]()
![]()
![]()
![]() )
)
![]() )
)
![]() (3.1)
(3.1)
![]() (3.2)
(3.2)
![]() )
)
![]() )
)
![]() K0n + k0)
K0n + k0)![]() (1.1)
(1.1)
![]() f
f![]() 1/2
1/2
![]() ) =
) = 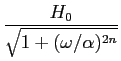 e-j
e-j![]() t0
t0![]() (2.1)
(2.1)
![]() tu(t)
tu(t)![]() (3.1)
(3.1)
![]()
![]() (3.2)
(3.2)
![]()
![]() )
)
![]() )
)
![]() )
)
![]() )
)
![]() t +
t + ![]() )
)![]() (4.1)
(4.1)
![]()
![]()
![]() )
)
![]() )
)
![]() )
)
![]() )
)
![]() ) =
) = ![$\displaystyle {{e^{j\omega}}\over {2[1+\cos (\omega)]}}$](img570.png)
![]() )
)