Subsecções
Esta secção do texto de apoio de Sinais e Sistemas contem os guiões das aulas práticas. As aulas práticas encontram-se divididas em 7 textos distintos a executar ao longo das 5 semanas de aulas de acordo com o calendário da tabela 2.
Tabela 2:
Calendário de realização dos trabalhos práticos de Sinais e Sistemas.
| Semana 1 |
TP1 e TP2 |
| Semana 2 |
TP3 |
| Semana 3 |
TP4 |
| Semana 4 |
TP5 |
| Semana 5 |
TP6 e TP7 |
|
Tanto a preparação como o relatório do trabalho prático serão entregues em formato electrónico através do sistema de tutoria electrónica(Moodle)4 tendo em conta as seguinte considerações:
- os ficheiros de texto com a preparação e com o relatório do trabalho deverão ser entregues em formato PDF;
- o relatório do trabalho prático será um ficheiro de arquivo (formato zip) com um m-file principal com o nome do trabalho em questão (p1.m, p2.m, etc...). Este m-file principal abrirá janelas com figuras e escreverá no ecrán resultados conforme solicitados no texto do trabalho sendo que a resposta a cada ponto deverá ser explícita e clara com legendas, eixos de abcissas e ordenadas com as respectivas legendas e unidades. Para cada caso deverá ser escolhido o método mais adequado para a representação dos resultados, incluindo vários gráficos na mesma figura (usando cores e legendas) ou sub-figuras;
- as preparac cões teóricas e os relatórios dos trabalhos práticos são entregues individualmente dentro do prazo definido no Moodel.
- a presença e entrega de todos trabalhos práticos é obrigatória.
Folha 1 - Introdução ao Matlab
Preparação teórica
Introdução
O Matlab é um ambiente de trabalho dedicado ao cálculo científico, métodos númericos e processamento de sinal. A principal característica do Matlab é que qualquer variável declarada é uma matriz portanto, em princípio, qualquer operação entre duas variáveis é uma operação matricial. Se a matriz for de dimensões 1×1
mathend000#, é um escalar e se for de dimensão 1×N
mathend000# é um vector. Pode também ser de dimensão superior a 2, i.e., pode ser uma matriz de 3, 4, 5 ou mais dimensões.
O Matlab é uma linguagem interpretada portanto, cada comando é executado quando se faz return. É no entanto possível executar funções e scripts, assim como executáveis exteriores através dum shell.
Considere a seguinte matriz 2×2
mathend000#,
A =
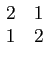
mathend000#
- a)
- calcule
B = A . A
mathend000#
- b)
- calcule C
mathend000# = produto ponto a ponto de A
mathend000# com A
mathend000#
- c)
- calcule A-1
mathend000#
- d)
- calcule o inverso ponto a ponto de A
mathend000#, 1/A
mathend000#.
- e)
- faça uma rotação vertical das linhas da matriz
- f)
- faça uma rotação horizontal das colunas da matriz
Trabalho prático
Exercício 1: declaração de matrizes e funções.
- declare um eixo temporal discreto
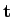 mathend000# de dimensão N = 1024
mathend000#, para
t1 = 0,..., tN = 2
mathend000# s, utilizando a função linspace [faça help linspace]. Qual o intervalo de tempo entre cada amostra em segundos ? Procure uma outra forma de fazer o mesmo eixo temporal sem utilizar a função linspace. E se quiser fazer um eixo temporal de [- 2, 2]
mathend000# segundos ?
mathend000# de dimensão N = 1024
mathend000#, para
t1 = 0,..., tN = 2
mathend000# s, utilizando a função linspace [faça help linspace]. Qual o intervalo de tempo entre cada amostra em segundos ? Procure uma outra forma de fazer o mesmo eixo temporal sem utilizar a função linspace. E se quiser fazer um eixo temporal de [- 2, 2]
mathend000# segundos ?
- construa agora uma função
s(t) = sin(x)
mathend000# onde
x =
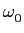 t
mathend000#. Se quisermos um seno de frequência f0 = 10
mathend000# Hz, como fazer ?
Construa o vector
t
mathend000#. Se quisermos um seno de frequência f0 = 10
mathend000# Hz, como fazer ?
Construa o vector 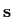 mathend000# em função do vector
mathend000# em função do vector 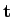 mathend000# do número anterior.
mathend000# do número anterior.
- queremos agora aumentar a amplitude da função s(t)
mathend000# para um valor A = 4.3
mathend000#.
- vamos agora construir uma nova função
g(t) = exp(-
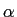 t)
mathend000#, onde
t)
mathend000#, onde 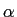 = 2
mathend000#. Determine o vector
= 2
mathend000#. Determine o vector 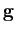 mathend000#.
mathend000#.
- utilizando a função plot represente os vectores
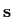 mathend000# e
mathend000# e 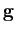 mathend000#, primeiro em duas figuras separadas, depois no mesmo gráfico (função hold)e em seguida em dois gráficos da mesma figura utilizando a função subplot. Coloque legendas nos eixos do tempo e amplitude e titulos no vários gráficos.
mathend000#, primeiro em duas figuras separadas, depois no mesmo gráfico (função hold)e em seguida em dois gráficos da mesma figura utilizando a função subplot. Coloque legendas nos eixos do tempo e amplitude e titulos no vários gráficos.
- determine agora a função
h(t) = g(t)s(t)
mathend000# [help .*]. Represente h(t)
mathend000#.
Exercício 2: funções particulares.
- construa a ``função'' Dirac unidade
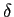 (n)
mathend000# que vale 1 para n = n0
mathend000# e vale zero para qualquer outro valor de n
mathend000#. Representa a função para vários valores de n0
mathend000#. Verifique a utilização da função zeros e ones do Matlab.
(n)
mathend000# que vale 1 para n = n0
mathend000# e vale zero para qualquer outro valor de n
mathend000#. Representa a função para vários valores de n0
mathend000#. Verifique a utilização da função zeros e ones do Matlab.
- faça o help da função function, que explica como realizar um função do Matlab. Realizar o exemplo da média.
- aplicar ao caso da ``função'' Dirac unidade, criando a função dirac-unit que tem como parâmetros de entrada o intervalo de definição [n1, n2]
mathend000# e a posição do Dirac n0
mathend000#. O que se passa se n0
mathend000# não se encontra entre n1
mathend000# e n2
mathend000# ?
- faça help for, que indica com fazer ciclos ``for''. Imagine que quer fazer um sinal no qual o Dirac unidade se repete com um período de 10 amostras (``pente de Diracs''). Como fazer, utilizando a função definida acima ? Represente.
- vamos agora fazer o mesmo sinal periódico utilizando as capacidades matriciais do Matlab, e em particular o comando matricial ``:'' . Para descobrir como funciona construa uma pequena matriz 3×3
mathend000#,
A =
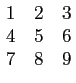
mathend000#
O separador é ``;''. Agora faça B=A(:). Qual o resultado ? Imagine como pode utilizar esta função para criar um sinal periódico tendo um período T0
mathend000#. Aplicar ao caso do Dirac unidade e compare a complexidade da solução do problema com o ciclo for.
- fazer agora a ``função'' degrau unidade definida no intervalo n1, n2
mathend000# e que vale zero até um certo instante n0
mathend000# a partir do qual passa a valer 1. O que se passa se n0
mathend000# não se encontra entre n1
mathend000# e n2
mathend000#. Construa e represente a function degrau-unit.
Folha 2 - Sinais discretos em Matlab
Preparação teórica
Exercício 1: considere o sinal
x[n] = u[n] - u[n - 20]
mathend000#.
- a)
- represente o sinal x[n]
mathend000#
- b)
- represente o sinal x[- n]
mathend000#
- c)
- represente o sinal x[8 - n]
mathend000#
- d)
- calcule a energia
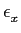 mathend000# do sinal x[n]
mathend000#
mathend000# do sinal x[n]
mathend000#
- e)
- calcule a energia px
mathend000# do sinal x[n]
mathend000#. Dificuldades ?
Exercício 2: considere o sinal
x[n] = exp[(-0.1+j0.3)n]
mathend000#.
- a)
- calcule o módulo
|x[n]|
mathend000# e a fase
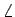 x[n]
mathend000# do sinal x[n]
mathend000#
x[n]
mathend000# do sinal x[n]
mathend000#
- b)
- represente o módulo e a fase de x[n]
mathend000# em função de n
mathend000#
Trabalho prático
Exercício 1: operações com sinais e funções.
- atraso temporal: partindo da função s(t)
mathend000# realizada no trabalho 1 construir uma função do Matlab capaz de realizar um atraso temporal de n0
mathend000# amostras, i.e., em entrada s[n]
mathend000# e em saída s[n - n0]
mathend000# onde n0
mathend000# é um número inteiro positivo ou negativo.
- dobragem no tempo: uma função muito útil, nomeadamente na operação de convolução é a dobragem temporal. Construir uma função do Matlab que permita obter como saída uma versão dobrada em relação ao eixo do tempo do sinal original, i.e., entra s[n]
mathend000# e sai s[- n]
mathend000# (explorar função fliplr).
- soma e produto - energia: explorar as funções sum e prod. Aplicar estas funções num modo eficiente de calcular a energia contida num sinal s[n]
mathend000#, dada por
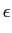
=
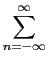 s2
s2[
n]
mathend000#
- potência: como é sabido, a potência é a energia por unidade de tempo de onde, utilizando o resultado anterior, pretende-se calcular a potência do sinal num determinado intervalo de N
mathend000# amostras (explorar a função mean, pode-se utilizar sempre ?).
Exercício 2:
Construa uma função porta a partir de dois degraus unidade, um atrasado em relação ao outro, de forma que
x[n] = u[n] - u[n - n0]
mathend000#
onde a função degrau unidade já foi estudada no trabalho anterior e o atraso temporal definido acima. Represente o resultado.
Faça agora uma dobragem em relação ao eixo do tempo, determinando x[- n]
mathend000#.
Exercício 3:
Gerar a função complexa
x[
n] = exp(-0.1+
j0.3)
n com -10
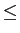 n
n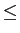
10
mathend000#
Representar o seu módulo, fase, parte real e parte imaginária numa única figura, particionada em quatro sub figuras. Cada figura terá o respectivo eixo, legendas e título [utilizar a função stem para a representação].
Folha 3 - Convolução
Preparação teórica
Exercício 1: considere o sinal
x[n] = u[n] - u[n - n0]
mathend000# como o sinal de entrada de um sistema de resposta impulsiva h[n]
mathend000# dada por
h[n] = anx[n]
mathend000#
onde a = 0.9
mathend000# é uma constante.
- a)
- represente x[n]
mathend000# e h[n]
mathend000#.
- b)
- efectue o cálculo literal do sinal de saída y[n]
mathend000# do sistema.
Exercício 2: considere a seguinte equação de diferenças representando a relação entre a entrada x[n]
mathend000# e a saída y[n]
mathend000# de um sistema linear invariante no tempo,
y[n] - y[n - 1] + 0.9y[n - 2] = x[n]
mathend000#
- a)
- calcule e faça um esboço da resposta impulsiva do sistema h[n]
mathend000#
- b)
- calcule e faça um esboço da resposta indicial do sistema a[n]
mathend000#
- c)
- trata-se de um sistema estável ? Porquê ?
Trabalho prático
Exercício 1: considere o sinal porta rectangular
x[n] = u[n] - u[n - 20]
mathend000# como o sinal de entrada de um sistema de resposta impulsiva h[n]
mathend000# dada por
h[n] = anx[n]
mathend000#
onde a = 0.9
mathend000# é uma constante.
- verifique o cálculo do exercício 1 a) da preparação com o Matlab criando uma função própria utilizando, em particular, as funções de atraso e dobragem já desenvolvidas no trabalho anterior.
- faça uma segunda verificação utilizando a função de convolução própria do Matlab.
- compare e comente os resultados em termos de diferenças e semelhanças, precisão e tempo de cálculo (funções tic, toc, etime, clock, cputime, etc...) assim como em termos de operações, função flops.
Exercício 2:
Temos uma sequência de pontos x[n]
mathend000# formando um sinal triangular de duração N = 10
mathend000# amostras e de amplitude A = 4
mathend000#. Construa x[n]
mathend000# de forma eficiente.
Filtre a sequência x[n]
mathend000# com um filtro h[n]
mathend000#, tal que
h[n] = exp-0.5n
mathend000#
- determine a resposta do filtro a um Dirac
- determine a resposta indicial do filtro
- calcule o sinal de resposta do filtro y[n]
mathend000# ao sinal de entrada x[n]
mathend000#
- construa versões atrasadas de n0
mathend000#=1, 2, 5 e 10 amostras do sinal de entrada x[n]
mathend000# e determine as respectivas respostas do filtro.
Exercício 3:
Considere a seguinte equação de diferenças representando a relação entre a entrada x[n]
mathend000# e a saída y[n]
mathend000# de um sistema linear invariante no tempo,
y[n] - y[n - 1] + 0.9y[n - 2] = x[n]
mathend000#
Calcule e represente com a ajuda da função filter comparando com os resultados obtidos na preparação:
- a resposta impulsiva do sistema
h[n];n = 0,..., 120
mathend000#.
- a resposta indicial do sistema
a[n];n = 0,..., 120
mathend000#.
- verifique numericamente que se trata de um sistema estável.
- calcule a energia do sinal.
Folha 4 - TF de sinais discretos no tempo
Preparação teórica
A TF discreta no tempo é, por definição, contínua na frequência e torna-se por isso difícil de representar em Matlab através de um número finito de pontos. Outro problema surge com a impossibilidade de calcular um número infinito de pontos discretos no tempo.
Exercício 1: considere o sinal
x[n] = 0.5nu[n]
mathend000# onde u[n]
mathend000# é a função degrau unidade.
- a)
- determine a expressão literal da TFDT X(f )
mathend000# de x[n]
mathend000#.
- b)
- faça um esboço de
|X(f )|
mathend000# e de
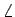 X(f )
mathend000#
X(f )
mathend000#
- c)
- admitindo agora que o sinal x[n]
mathend000# é finito com N
mathend000# amostras, calcule a expressão literal de X(f )
mathend000#.
- d)
- represente o módulo e a fase de X(f )
mathend000# da alínea c) e compare com os esboços da alínea b).
Exercício 2: utilizando a TFDT demonstre que se
y[n] = h[n]x[n]
mathend000# então podemos escrever que
Y(f )= H(f )X(f )
mathend000#, onde Y(f )
mathend000#, H(f )
mathend000# e X(f )
mathend000# são as TFDT de y[n]
mathend000#, h[n]
mathend000# e x[n]
mathend000#, respectivamente.
Trabalho prático
Exercício 1: considere o sinal
x[n] = 0.5nu[n]
mathend000# onde u[n]
mathend000# é a função degrau unidade.
- a)
- represente x[n]
mathend000#
- b)
- visto que o sinal x[n]
mathend000# é infinito no tempo somos levados apenas a calcular a representação gráfica da expressão calculada na preparação utilizando um número de pontos em f
mathend000# razoável calcule e represente: 1) o módulo de X(f )
mathend000#, 2) a fase de X(f )
mathend000#, 3) a parte real e a parte imaginária de X(f )
mathend000#, colocando os eixos as legendas em todos os gráficos.
Exercício 2: vamos agora admitir que o sinal x[n]
mathend000# do exemplo anterior é finito com N = 20
mathend000# amostras.
- a)
- calcule X(f) utilizando a implementação em Matlab da expressão de definição do TF de um sinal discreto em modo eficiente [ o somatório pode ser representado como uma multiplicação matricial ].
- b)
- represente X(f )
mathend000# em módulo e fase
- c)
- compare com os resultados do exercício 1 e com os resultados da preparação.
Exercício 3: considere o sinal
p[n] = u[n] - u[n - n0]
mathend000#.
- a)
- para n0 = 10
mathend000#, calcule e represente P(f )
mathend000# utilizando a implementação eficiente do execício anterior
- b)
- repita a alínea anterior com n0 = 20
mathend000#. Qual a diferença no resultado ? Explique.
Exercício 4: considere agora um novo sinal
y[n] = x[n]p[n]
mathend000#, onde x[n]
mathend000# é o sinal do exercício 1.
- a)
- calcule e represente Y(f )
mathend000#.
- b)
- prove numericamente que
Y(f )= X(f ) * P(f )
mathend000#. Explique as dificuldades encontradas.
Folha 5 - Densidade espectral
Preparação teórica
Exercício 1: sendo que rxy[n]
mathend000# é a correlação entre os sinais x[n]
mathend000# e y[n]
mathend000#, demonstre que
rxy[n] = y[l] * x[- l]
mathend000#, i.e., que a correlação entre dois sinais é igual à convolução de um deles com a versão dobrada em relação ao tempo do outro.
Exercício 2: dado um sinal
x[n] = anu[n]
mathend000#, onde a
mathend000# é um número real < 1
mathend000# e u[n]
mathend000# é a função degrau unidade,
- a)
- calcule a expressão da sua função de autocorrelação rxx[l]
mathend000#,
- b)
- calcule a sua densidade espectral de potência Pxx(f )
mathend000#
- c)
- determine e represente em módulo e fase de Pxx(f )
mathend000#
- d)
- calcule agora directamente a TFDT X(f )
mathend000# de x[n]
mathend000# e represente o quadrado do seu módulo
|X(f )
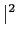 mathend000# e compare o resultado obtido com o gráfico da alínea anterior.
mathend000# e compare o resultado obtido com o gráfico da alínea anterior.
Exercício 3: considere o sistema linear de coeficientes constantes descrito pelo relação entrada-saída
|
y[n] = 0.8y[n - 1] - x[n]
|
(B.-5.1) |
mathend000#
- a)
- determine e represente (módulo e fase) da função de transferência H(f )
mathend000# do sistema.
- b)
- qual a atenuação e atraso de fase sofrido por um sinal x[n]
mathend000# sinusoidal com uma pulsação de 0.05
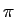 mathend000# rd/s quando passado pelo sistema de equação entrada-saída (C-7.2).
mathend000# rd/s quando passado pelo sistema de equação entrada-saída (C-7.2).
Trabalho prático
Exercício 1: utilização das funções do Matlab para a correlação e convolução:
- a)
- considere e represente dois sinais discretos
x[n] = 0.9nu[n]
mathend000# e
y[n] = u[n] - u[n - 20]
mathend000#.
- b)
- calcule e represente a sua função de correlação rxy[n]
mathend000#.
- c)
- utilizando agora os mesmos sinais x
mathend000# e y
mathend000# e o produto de convolução com um dos sinais dobrados no tempo, demonstre que se obtem a mesma função de correlação rxy
mathend000#.
Exercício 2: utilizando o sinal x[n]
mathend000# do exercício anterior calcule:
- b)
- a sua função de autocorrelação rxx[l]
mathend000#.
- c)
- determine e represente em módulo e fase da TF de rxx[l]
mathend000#, Pxx(f )
mathend000# utilizando a implementação em Matlab da expressão de definição do TF de um sinal discreto em modo eficiente no seu intervalo de definição.
- d)
- calcule agora directamente a TF X(f )
mathend000# de x[n]
mathend000# e represente o quadrado do seu módulo
|X(f )
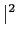 mathend000# e compare o resultado obtido com o gráfico da alínea anterior.
mathend000# e compare o resultado obtido com o gráfico da alínea anterior.
Exercício 3: considere o sistema linear de coeficientes constantes descrito pelo relação entrada-saída
y[n] = 0.8y[n - 1] - x[n]
mathend000#
- a)
- determine e represente a função de transferência H(f )
mathend000# do sistema.
- b)
- calcule e represente a resposta do sistema ao sinal de entrada
x[n] = cos(0.05
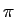 n)u[n]
mathend000#.
n)u[n]
mathend000#.
Folha 6 - Filtros I
Preparação teórica
Pretende-se calcular um filtro FIR de tipo passa-baixo de frequência de corte fc
mathend000# e de atenuação A
mathend000# dB entre a banda passante e a banda de corte.
- a partir do filtro passa-baixo ideal com as características pretendidas, calcule a forma literal da sua resposta impulsiva discreta
- implemente a resposta impulsiva discreta e torne-a finita através de uma janela de observação rectangular (função porta) de duração M
mathend000# amostras. Calcule o espectro de amplitude do sinal obtido. Responde às características desejadas ? Explique porquê ?
- consegue melhorar as características do filtro aumentand o valor de M
mathend000# ? Porquê ?
Trabalho prático
Exercício 1: uma das formas de especificar um filtro é através de uma equação de diferenças. Por exemplo a equação
| y[n] |
= |
0.0181x[n] + 0.0543x[n - 1] + 0.0543x[n - 2] + 0.0181x[n - 3] + 1.76y[n - 1] - |
|
| |
|
-1.1829y[n - 2] + 0.2781y[n - 3] |
|
representa um filtro de terceira ordem.
- a)
- calcule e represente o seu módulo e fase e demonstre que se trata de um filtro passa-baixo.
- b)
- qual a sua frequência de corte ? E a sua banda passante ?
- c)
- utilizando a expressão da TFI determine a resposta impulsiva do sistema. Como pode obter essa resposta de outra forma utilizando funções próprias do Matlab ? Compare.
Exercício 2: pretende-se calcular um filtro FIR com as seguintes características:
- tipo: passa baixo
- frequência de corte: fc = 100
mathend000# Hz.
- oscilação máxima na banda passante: 0.25 dB
- atenuação mínima na banda de corte: 50 dB
- largura da banda de transição: 40 Hz
- frequência de amostragem: fs
mathend000# = 1000 Hz
- implemente a resposta impulsiva discreta calculada na preparação e torne-a finita através de uma janela de observação rectangular (função porta) de duração M = 25
mathend000# amostras. Calcule e represente o espectro de amplitude e de fase do filtro obtido e caracterize-o em termos dos parâmetros desejados
- aumente o valor de M
mathend000# e volte a calcular o espectro. Consegue obter o filtro que se pretende ? Porquê ?
- substitua a função porta por uma função de Hanning, Hamming e Blackman. Consegue nesse caso obter o resultado pretendido ? Caracterize o filtro finalmente obtido.
- explique como obter desde logo o tipo de janela necessário de acordo com as características do filtro desejado.
Folha 7 - Filtros II
Preparação teórica
Leitura do capítulo 5.7 do texto de apoio de Sinais e Sistemas.
Trabalho prático
Exercício 1: pretende-se desenhar um filtro IIR a partir dos filtros analógicos tipo Butterworth, Chebyshev ou Elíptico, especificado pela sua resposta em frequência com as seguintes características:
- tipo: passa banda
- frequências de corte: f1 = 100
mathend000# e f2 = 300
mathend000# Hz.
- oscilação máxima na banda passante: 2 dB
- atenuação mínima na banda de corte: 80 dB
- largura da banda de transição: 30 Hz
- frequência de amostragem: fs
mathend000# = 1000 Hz
- calcule a ordem mínima de cada um dos tipos de filtro que permitem realizar este filtro
- calcule os coeficientes do vários tipos de filtro
- calcule e represente a no mesmo gráfico as respostas em frequência em fase dos vários tipos de filtro. Determina quais são aqueles que melhor respondem aos critérios pedidos.
Exercício 2: utilizando o filtro mais complexo e o menos complexo do exercício anterior utilize-os para filtrar o seguinte sinal:
y(
t) = sin(2
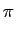 f1t
f1t) + sin(2
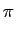 f2t
f2t) + sin(2
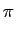 f3t
f3t) + sin(2
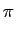 f4t
f4t)
mathend000#
com os seguinte valores de frequência em Hz f1 = 90
mathend000#, f2 = 105
mathend000#, f3 = 115
mathend000# e f4 = 118
mathend000#.
- utilizando um filtro do tipo recursivo no tempo.
- utilizando filtragem no domínio da frequência
truemm
Sergio Jesus
2008-12-30
![]()
![]()
![]() t
t
![]()
![]()
![]() t)
t)
![]() = 2
= 2
![]()
![]()
![]()
![]() (n)
(n)
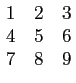
![]()
![]() x[n]
x[n]
![]() =
= ![]() s2[n]
s2[n]
![]() n
n![]() 10
10
![]() X(f )
X(f )
![]()
![]()
![]()
![]() n)u[n]
n)u[n]
![]() f1t) + sin(2
f1t) + sin(2![]() f2t) + sin(2
f2t) + sin(2![]() f3t) + sin(2
f3t) + sin(2![]() f4t)
f4t)