mathend000#.
É facilmente compreensível que a noção de quantidade de informação seja uma questão central em problemas de telecomunicações. O objectivo primário de um sistema de comunicação não é mais do que transmitir informação de um ponto para o outro. Foi Claude Shannon em 1940 que, pela primeira vez, introduziu a possibilidade de quantificar a quantidade de informação, e assim revolucionou a nossa forma de ver a problemática das comunicações.
Porém não basta que uma determinada mensagem seja fielmente discretizada no tempo, é também necessário que ela seja discretizada na sua amplitude. Isto é, s(t)
mathend000# é à partida uma função real de variável real t
mathend000#. Uma vez que se procedeu à discretização da variável tempo t
mathend000#, ela passou a ser uma função real de variável discreta k
mathend000#, que toma valores inteiros. Teoricamente uma função real pode tomar um número infinito de valores o que, utilizando um sistema binário, necessitaria na prática um número infinito de bits para ser representado. O processo que permite reduzir o número de níveis que pode tomar a amplitude de uma determinada mensagem chama-se quantificação. A quantificação é um processo que introduz inevitavelmente alguma distorção.
Finalmente, quando a mensagem que se pretende transmitir se encontra discretizada, seja no tempo seja na amplitude, trata-se de determinar qual o melhor modo de representar os níveis obtidos após discretização de forma a minimizar, tanto quanto possível, a quantidade de dados a transmitir, sem que no entanto haja perda de informação. A este último processo chama-se codificação sem ruído ou compressão de dados. Talvez esta última etapa não seja muito clara e por isso vamos dar um exemplo simples. Vamos imaginar que uma determinada mensagem é quantificada entre -10 e +10 volts utilizando 1024 níveis discretos. Admitindo que o sinal é em geral de média nula, é provável que uma estatística demonstre que os valores dos níveis centrais (em torno a 0) são mais prováveis do que os níveis perto dos -10 ou dos +10 volts. Compreende-se então facilmente que seria vantajoso para o sistema de comunicações que os níveis centrais fossem codificados com menos bits, enquanto os níveis menos prováveis (que ocorrem menos frequentemente) fossem codificados com mais bits. Este processo de atribuição de códigos mais curtos a símbolos mais prováveis e de códigos mais longos a símbolos menos prováveis, consiste um exemplo simples da utilização eficiente da codificação para a diminuição do volume de dados a transmitir, aumentando assim a eficiência do sistema de transmissão. Trata-se de alguma forma de uma compressão de dados, cujo exemplo mais familiar de todos é o algoritmo de Lempel-Ziv universalmente utilizado nos programas de ``zipagem'' em informática.
A entropia é uma forma de medir a quantidade de informação. Intuitivamente uma mensagem tem tanta mais informação quanto maior for o seu grau de aleatoriadade ou imprevisibilidade. Por exemplo, se dissermos: ''o sol nasceu esta manhã''. Temos aqui uma menssagem com uma certa quantidade de informação. Agora se dissermos: ''houve um terramoto em Lisboa.'' Qual das duas frases tem mais informação ? Intuitivamente seremos levados a dizer que a segunda tem mais informação que a primeira. Isto, porque a segunda mensagem era mais imprevisível, ou seja representa um acontecimento que ocorre menos vezes que o da primeira mensagem. A entropia tenta traduzir uma forma de quantificar este conceito. Assim, por exemplo, a entropia ou quantidade de informação da variável aleatória x
mathend000# de probabilidade pX(x)
mathend000#, é definida por
H(x) = E[- log2pX(x)] = - 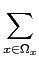 pX(x)log2pX(x). pX(x)log2pX(x). |
(4-1.01) |
Nesta equação percebemos o porquê da densidade de probabilidade e do sinal de menos, pois a entropia deverá ser tanto maior quanto menos provável for o sinal, e também percebemos o porquê da esperança matemática E[.]
mathend000#, que realiza uma ``média'' sobre todas as tiragens possíveis. Mas de onde vem o log2
mathend000# ? A introdução do logaritmo está ligada com o facto de que se considerarmos dois processos estocásticos independentes X
mathend000# e Y
mathend000#, a informação do acontecimento conjunto de X
mathend000# e de Y
mathend000# deverá ser simplesmente a soma das quantidades de informação de um e do outro (o logaritmo do produto é a soma dos logaritmos!). Assim deverá haver um logaritmo tal que
| H(x, y) |
= |
E[- log2pXY(x, y)] |
(4-1.02) |
| |
= |
E[- log2pX(x) - log2pY(y)] |
(4-1.03) |
| |
= |
H(x) + H(Y), |
(4-1.04) |
onde
pXY(x, y)
mathend000# não é mais do que a densidade de probabilidade conjunta das va's X
mathend000# e Y
mathend000#, tal que, visto que as va's são independentes,
pXY(x, y) = pX(x)pY(y)
mathend000#. Para o caso do alfabeto binário, formado de 0 e 1's, com probabilidades p
mathend000# e 1 - p
mathend000# respectivamente, a entropia total é dada por
| Hb(p) = - p log2p - (1 - p)log2(1 - p) |
(4-1.05) |
que se encontra representada na figura 4.1 em função da probabilidade p
mathend000#.
Figura 4.1:
entropia do alfabeto binário.
|
|
Podemos ver nesta figura que se a probabilidade p
mathend000# do símbolo 0 for nula então quer dizer que todos os símbolos serão iguais a 1 e imprevisibilidade será nula e portanto a quantidade de informação ou entropia também. O mesmo acontece para p = 1
mathend000#. Inversamente se p = 0.5
mathend000#, a probabilidade de ter 0 ou 1 é igual e portanto a imprevisibilidade será máxima coincidindo com a quantidade de informação e com a entropia máxima.
Quantificação é o processo de representação de uma fonte de dados analógicos num conjunto finito de níveis. Como já dissemos, este processo introduz necessariamente alguma distorção e perda de informação. De uma forma geral a quantificação pode ser uniforme ou não uniforme. Na quantificação uniforme o passo de quantificação, i.e., a diferença entre dois níveis contíguos é constante entre o valor mínimo e o valor máximo. No caso de quantificadores não uniformes, pelo seu lado, o nível de quantificação não é constante. Na análise da quantificação pode-se representar o sinal a quantificar por uma variável aleatória (v.a.) X
mathend000#, de lei pX(x)
mathend000#. O processo de quantificação consiste na divisão do domínio de X
mathend000# em N
mathend000# intervalos contíguos onde cada intervalo de quantificação Rn
mathend000# é representado por um valor 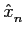 mathend000#. Assim cada vez que a v.a. X
mathend000#, de valor x
mathend000#, à entrada do quantificador pertence ao intervalo Rn
mathend000#, a saída do quantificador toma o valor
mathend000#. Assim cada vez que a v.a. X
mathend000#, de valor x
mathend000#, à entrada do quantificador pertence ao intervalo Rn
mathend000#, a saída do quantificador toma o valor 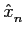 mathend000#. O erro quadrático médio dado por
mathend000#. O erro quadrático médio dado por
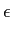 |
= |
E[(x - 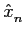 )2] )2] |
|
| |
= |
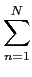 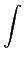 (x - (x -  )2pX(x)dx, )2pX(x)dx, |
(4-2.01) |
caracteriza, em média, o erro quadrático de quantificação cometido ao substituir o valor real x
mathend000# pelo seu valor quantificado 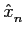 mathend000#. O valor (4-2.1) toma o nome de ruído de quantificação. Assim, a relação sinal-ruído de quantificação escreve-se (SQNR=signal to quantization noise ratio), é
mathend000#. O valor (4-2.1) toma o nome de ruído de quantificação. Assim, a relação sinal-ruído de quantificação escreve-se (SQNR=signal to quantization noise ratio), é
SQNRdB = 10 log10![$\displaystyle {{E[X^2]}\over {\epsilon}}$](img208.png) , , |
(4-2.02) |
onde E[X2]
mathend000# representa a esperança matemática do quadrado da v.a. X
mathend000#, i.e., a sua variância se for de média nula.
Quantificação uniforme
No processo de quantificação uniforme o domínio de discretização é dividido em intervalos iguais, i.e.,
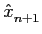 -
- 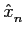 =
= 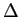 mathend000# é uma constante
mathend000# é uma constante 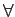 n
mathend000#. Se o domínio a discretizar não for limitado, então o primeiro e o último intervalos de quantificação são infinitos, i.e., as regiões de discretização serão dadas por
n
mathend000#. Se o domínio a discretizar não for limitado, então o primeiro e o último intervalos de quantificação são infinitos, i.e., as regiões de discretização serão dadas por
| R1 |
= |
] -  , a] , a] |
|
| R2 |
= |
]a, a + 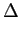 ] ] |
|
| R3 |
= |
]a + 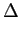 , a + 2 , a + 2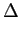 ] ] |
|
| |
 |
|
(4-2.03) |
| RN |
= |
]a + (N - 2)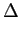 , ,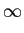 [, [, |
(4-2.04) |
demonstra-se facilmente que o nível a associar com cada intervalo de quantificação é dado pelo valor médio de cada intervalo, assim
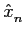 = a + (n - 2) = a + (n - 2)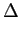 + + 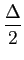 , , |
(4-2.05) |
este ponto é chamado a centróide do intervalo e não é mais do que
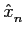 = E[X|X
= E[X|X 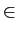 Rn]
mathend000#. Será fácil determinar que a função de quantificação
Q(x) =
Rn]
mathend000#. Será fácil determinar que a função de quantificação
Q(x) = 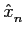 , n
, n 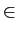 [1, N]
mathend000# é uma função em escada, dependente dos dois parâmetros a
mathend000# e
[1, N]
mathend000# é uma função em escada, dependente dos dois parâmetros a
mathend000# e 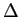 mathend000#.
mathend000#.
Como já foi referido acima, o erro (ou ruído) de quantificação é devido à diferença entre o valor real do sinal no instante k
mathend000#, x(k)
mathend000# e o seu valor quantificado 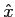 (k)
mathend000#, que pode ser estimado considerando que, se o número de níveis N = 2R
mathend000# é suficientemente elevado, o sinal amostrado pode-se representar como
(k)
mathend000#, que pode ser estimado considerando que, se o número de níveis N = 2R
mathend000# é suficientemente elevado, o sinal amostrado pode-se representar como
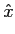 (k) = x(k) + q(k), (k) = x(k) + q(k), |
(4-2.06) |
onde q(k)
mathend000# representa o ruído de quantificação, suposto uniforme no intervalo
[- 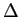 /2,
/2,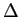 /2]
mathend000#. Ora é sabido que a potência do ruído pode ser expressa pela sua variância, o que para uma v.a. uniforme é
/2]
mathend000#. Ora é sabido que a potência do ruído pode ser expressa pela sua variância, o que para uma v.a. uniforme é
de onde podemos calcular a relação sinal-ruído de quantificação (SQNR) em dB, como sendo
| SQNRdB |
= |
10 log10[3 x 4R![$\displaystyle {{E[X^2]} \over {x_{\rm max}^2}}$](img218.png) ] ] |
|
| |
= |
10 log10[3 x 4RE[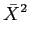 ]] ]] |
|
| |
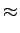 |
4.8 + 6R + 10 log10E[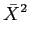 ], ], |
(4-2.08) |
onde
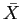 = X/xmax
mathend000# é o valor normalizado do sinal x(k)
mathend000#. A taxa de transmissão do sinal codificado é (no mínimo) fsR
mathend000#, o que significa que na prática é quase sempre superior a 1.5fsR
mathend000#.
= X/xmax
mathend000# é o valor normalizado do sinal x(k)
mathend000#. A taxa de transmissão do sinal codificado é (no mínimo) fsR
mathend000#, o que significa que na prática é quase sempre superior a 1.5fsR
mathend000#.
Neste caso o intervalo de quantificação não é constante. É óbvio que uma zona de valores onde o sinal é mais provável deverá ter mais níveis do que uma região onde o sinal é pouco provável. Assim, este método de quantificação permite normalmente obter um maior desempenho que o caso uniforme. Prova-se com efeito que os intervalos e níveis de quantificação são dados de forma óptima através das condições de Lloyd-Max que se escrevem
de onde podemos concluir que os níveis de quantificação óptimos são dados pelas centroides e os limites de quantificação de cada região são dados pelos pontos médios entre cada par de centroides. A resolução do sistema de equações (4-2.10) faz-se de modo iterativo partindo de um conjunto inicial de centroides e calculando iterativamente o ruído de distorção, até que não haja uma diminuição significativa dessa distorção entre um ponto e o seguinte.
Já vimos como colocar uma mensagem sob a forma de uma sequência de valores ou símbolos que forma uma representação discreta da informação emitida pela fonte. Vamos agora tratar do problema de como codificar de forma óptima esta sequência de símbolos numa sequência de digitos binários. Tendo em conta que o alfabeto utilizado pela fonte é geralmente finito, o problema da codificação torna-se um problema relativamente fácil. No entanto isto só é verdade quando os símbolos são estatisticamente independentes entre si, i.e., quando o sistema não tem memória - diz-se nesse caso que temos uma fonte discreta sem memória. Infelizmente, na prática, poucas fontes de mensagens podem ser consideradas como sendo fontes discretas sem memória.
O exemplo clássico consiste em considerar uma fonte discreta sem memória que produz um símbolo cada 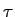 mathend000# segundos. Cada um dos símbolos é selecionado de um alfabeto finito com L
mathend000# símbolos
xn;n = 1,..., L
mathend000#, com a probabilidade p(xn)
mathend000#. Assim a entropia da fonte, de acordo com (4-1.1), é dada por
mathend000# segundos. Cada um dos símbolos é selecionado de um alfabeto finito com L
mathend000# símbolos
xn;n = 1,..., L
mathend000#, com a probabilidade p(xn)
mathend000#. Assim a entropia da fonte, de acordo com (4-1.1), é dada por
H(x) = - 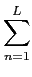 p(xn)log2p(xn). p(xn)log2p(xn). |
(4-3.01) |
Se os símbolos forem igualmente prováveis temos que
p(xn) = 1/L
mathend000# e então
| H(x) |
= |
- 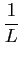 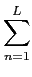 log2 log2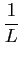 |
|
| |
= |
log2L, |
(4-3.02) |
o que representa o valor máximo que pode tomar H(x)
mathend000# em (4-3.1), e que é o número de bits médio necessário para representar cada símbolo do alfabeto. A taxa de transmissão é então de H(x)/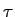 mathend000# bits/s. Existem essencialmente dois grandes grupos de métodos de codificação para fontes discretas sem memória, que são: codificação com palavras de comprimento fixo e codificação com palavras de comprimento variável.
mathend000# bits/s. Existem essencialmente dois grandes grupos de métodos de codificação para fontes discretas sem memória, que são: codificação com palavras de comprimento fixo e codificação com palavras de comprimento variável.
Neste caso utiliza-se um número de bits R
mathend000# fixo para cada símbolo. De acordo com este esquema de codificação, a cada símbolo corresponderá um único conjunto de R
mathend000# bits. Dado que temos L
mathend000# símbolos e, admitindo que L
mathend000# é uma potência de 2, o número de bits necessário é dado por
R = log2L
mathend000#. Se L
mathend000# não for uma potência de 2 então o número de bits necessário será
R = int[log2L] + 1
mathend000#, onde int
mathend000# significa ``o maior inteiro inferior a''. É óbvio que se
H(x)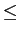 log2L
mathend000# teremos que
R
log2L
mathend000# teremos que
R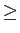 H(x)
mathend000#. Na prática um bom esquema de codificação é aquele que se aproxima o mais possível da entropia, e portanto H(x)/R
mathend000# é uma medida da eficiência do esquema de codificação. Existem métodos alternativos que consistem em codificar não cada símbolo individualmente mas sim sequências de símbolos (um exemplo típico é um código fonte no qual as palavras while do, etc se encontram frequentemente repetidas). Assim pode-se melhorar a eficiência do esquema de codificação aumentando o número de símbolos por grupo tanto quanto se pretender.
H(x)
mathend000#. Na prática um bom esquema de codificação é aquele que se aproxima o mais possível da entropia, e portanto H(x)/R
mathend000# é uma medida da eficiência do esquema de codificação. Existem métodos alternativos que consistem em codificar não cada símbolo individualmente mas sim sequências de símbolos (um exemplo típico é um código fonte no qual as palavras while do, etc se encontram frequentemente repetidas). Assim pode-se melhorar a eficiência do esquema de codificação aumentando o número de símbolos por grupo tanto quanto se pretender.
Alternativamente, existem esquemas nos quais a relação entre a representação em bits de cada símbolo não é única. Isto significa que no alfabeto podem coexistir um conjunto de símbolos cuja representação é única (os mais frequentes) e um outro conjunto de símbolos representados pelo mesmo conjunto de bits (os muito pouco frequentes). É claro que este esquema de codificação não permite a recuperação de toda a informação emitida pela fonte no momento de descodificação. Trata-se aqui de uma codificação que introduz ruído de codificação e portanto perda de informação. O problema na prática é de controlar o ruído de quantificação dentro de níveis aceitáveis obtendo em troca um forte aumento da compactação da informação que se traduz numa eficiência alta e portanto uma alta taxa de transmissão efectiva.
Quando os símbolos emitidos pela fonte não são equiprováveis torna-se óbvio que o esquema de codificação mais apropriado deverá ter códigos de comprimento variável: os símbolos mais frequentes deverão ter códigos com menos bits e vice-versa. O exemplo mais conhecido é o código Morse que já na época utilizava códigos mais curtos para as letras mais frequentes do alfabeto. Um problema óbvio desde logo é que as letras mais frequentes por exemplo em inglês não serão sempre as mais frequentes em português o que leva inevitavelmente a perdas de eficiência quando de mudanças de língua. Um problema que se coloca na prática quando da codificação com palavras de comprimento variável é que por vezes não podemos saber imediatamente no receptor se uma dada sequência de bits forma vários símbolos codificados com códigos curtos ou símbolos codificados com códigos longos, dado que utilizando digitos binários, utilizar o `1' para o A, `00' para o B, `01' para o C e `10' para o D, a sequência `001001' não nos permite determinar unicamente quais os símbolos emitidos. Claramente temos B como primeiro símbolo mas em seguida não sabemos se é ABA ou CB. Na prática temos que ter a certeza que o código escolhido não contém ambiguidades e pode ser unicamente e instantanemante descodificado. Desde já podemos notar que existe uma condição de base que é chamada a Condição do prefixo: e que consiste em afirmar que nenhum código deverá ser o prefixo de um outro código. Pode-se efectivamente demonstrar que códigos com palavras de comprimento variável que satisfazem a condição do prefixo são eficientes para qualquer fonte discreta sem memória com símbolos não equiprováveis. O algoritmo de Huffman permite construir tais códigos e é muito importante na prática.
Algoritmo de codificação de Huffman
O método proposto por Huffman em 1952 baseia-se no princípio de atribuir de forma progressiva os códigos mais longos aos símbolos menos prováveis até aos símbolos mais prováveis, evitando os prefixos. Desde logo se pode constatar que para construir um esquema de codificação com o algoritmo de Huffman é necessário dispôr das probabilidades de cada símbolo. O procedimento inicia-se concatenando os dois símbolos menos prováveis construindo um novo símbolo cuja probabilidade é igual à soma das probabilidades dos dois símbolos iniciais. Este processo prossegue até ficarmos com um único símbolo de probabilidade 1. Obtem-se assim uma árvore contendo todas as combinações dos símbolos existentes. Começa-se depois pela raíz da árvore alocando os digitos `0' e `1' aos dois símbolos mais prováveis (e que assim terão o código mais curto); em seguida os dois símbolos que formam, por exemplo o símbolo codificado com o `0' serão codificados com `00' e `01', da mesma forma para o outro ramo com `10' e `11' e assim sucessivamente aumentando o número de digitos do código à medida que se diminui a probabilidade do símbolo e garantido que a condição do prefixo é satisfeita. Talvez a forma mais simples seja, neste caso, a de aplicar o algoritmo de codificação de Huffman num exemplo.
Exemplos: consideremos um alfabeto de L = 7
mathend000# símbolos
{x1,..., x7}
mathend000# que ocorrem com as probabilidades indicadas na tabela 4.1.
Tabela 4.1:
exemplo de aplicação do algoritmo de codificação de Huffman (exemplo 3.3.1 de [2]).
| símbolos |
probabilidade |
informação |
Código |
| x1
mathend000# |
0.35 |
0.5301 |
00 |
| x2
mathend000# |
0.30 |
0.5211 |
01 |
| x3
mathend000# |
0.20 |
0.4644 |
10 |
| x4
mathend000# |
0.10 |
0.3322 |
110 |
| x5
mathend000# |
0.04 |
0.1858 |
1110 |
| x6
mathend000# |
0.005 |
0.03882 |
11110 |
| x7
mathend000# |
0.005 |
0.03882 |
11111 |
| Total |
1 |
2.11 |
- |
|
A aplicação do algoritmo faz-se através da árvore da figura 4.2 da qual podemos extrair os códigos indicados na última coluna da tabela 4.1. Podemos verificar que estes códigos efectivamente asseguram a condição do prefixo. Podemos ainda notar que a codificação de Huffman não é única pois a atribuição do bit `0' ao ramo superior e `1' ao ramo inferior é puramente arbitrária, assim como a junção de x1
mathend000# e x2
mathend000# e o resultado com x3'
mathend000# de probabilidade 0.35 ou alternativamente x2
mathend000# com x3'
mathend000# e o resultado com x1
mathend000#. Deixamos ao cuidado do leitor a verificação de que a nova codificação assim obtida atinge o mesmo factor de qualidade. A informação contida em cada símbolo i
mathend000# é dada por
pilog2pi
mathend000# e encontra-se calculada na terceira coluna da tabela 4.1 e de onde podemos deduzir a quantidade de informação total
H(x) = 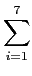 pilog2pi = 2.11. pilog2pi = 2.11. |
(4-3.03) |
Para ter uma ideia do grau de eficiência deste código devemos comparar este número com aquele dado pelo número de bits médio
R = 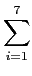 piNi = 2.21, piNi = 2.21, |
(4-3.04) |
onde Ni
mathend000# é um número de bits utilizado para codificar o símbolo xi
mathend000#. Chegamos assim ao factor de qualidade
Q = H(x)/R = 0.954
mathend000#, ou seja, uma eficiência de 95.4%. Em termos de comparação, se tivessemos utilizado um algoritmo com palavras de comprimento fixo, teriam sido necessários 3 bits por símbolo e por isso teriamos R = 3
mathend000#, o que daria um factor de eficiência
Q = 2.11/3 = 0.7
mathend000# ou 70%.
Figura 4.2:
árvore de aplicação do algoritmo de Huffman no exemplo da tabela 4.1.
|
|
Voltamos agora ao caso geral no qual a fonte não é sem memória, i.e., o caso em que os símbolos emitidos não são estatisticamente independentes uns dos outros, porém consideraremos sempre o caso em que a sequência de símbolos será considerada estacionária. Ou seja, o processo aleatório discreto associado à fonte não é branco mas é estacionário. Aqui o problema é singularmente mais complicado dada a dependência estatística entre símbolos, que não nos permite determinar a entropia (e portanto o número mínimo de bits necessário), de forma directa. Felizmente pode-se definir a entropia de um alfabeto de uma fonte estacionária através da definição da entropia de um bloco de símbolos. Assim, seja a entropia do bloco de símbolos
{X1, X2,..., Xk}
mathend000#,
H(X1, X2,..., Xk) = 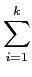 H(Xi|X1, X2,..., Xi-1), H(Xi|X1, X2,..., Xi-1), |
(4-3.05) |
onde
H(Xi|X1, X2,..., Xk)
mathend000# é a entropia condicional do símbolo Xi
mathend000# dados os símbolos anteriores
Xn;n = 1,..., i - 1
mathend000#. A entropia por símbolo dentro do conjunto de k
mathend000# símbolos, define-se como sendo
Hk(X) = 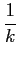 H(X1, X2,..., Xk). H(X1, X2,..., Xk). |
(4-3.06) |
Finalmente a entropia do alfabeto escreve-se como sendo a entropia do bloco k
mathend000# quando
k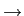
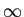 mathend000#,
mathend000#,
H(X) = 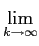 Hk(X) = Hk(X) = 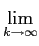 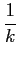 H(X1, X2,..., Xk). H(X1, X2,..., Xk). |
(4-3.07) |
O papel da definição da noção de entropia no caso estacionário é essencial pois permite estabelecer uma métrica da eficiência da codificação. A partir daqui prova-se que uma codificação eficiente de uma fonte discreta estacionária com memória é possível através da representação de largos blocos de símbolos por códigos. Para cada um dos blocos pode (e deve) ser utilizado o algoritmo de Huffman com código de palavras de comprimento variável. De notar no entanto que para que isso seja possível será necessário conhecer as densidades de probabilidade conjuntas dos símbolos contidos no mesmo bloco, o que nem sempre acontece de forma directa e requere frequentemente na prática uma fase de amostragem para obter uma estimação empírica dessas probabilidades. Para obviar este problema da necessidade da estimação das probabilidades a priori foi proposto o algoritmo de Lempel-Ziv.
Algoritmo de Lempel-Ziv
Este algoritmo é independente das propriedades estatísticas dos dados e por isso tem um carácter universal. Este algoritmo procede separando a sequência emitida pela fonte em blocos de comprimento variável, chamadas frases. Uma nova frase é criada cada vez que ela difere no seu último símbolo de uma outra frase formada anteriormente. As frases são colocadas num dicionário juntamente com o respectivo índice de início de frase na mensagem. Quando toda a mensagem foi lida, atribui-se sequencialmente um código a cada uma das frases formado pela localização da frase na mensagem acrescentada da última letra em que cada mensagem difere das outras já classificadas no dicionário. Esta etapa de codificação é inicializada começando com o código `0000' (no número de bits necessário para o comprimento do dicionário). No descodificador constrói-se a tabela a partir dos códigos recebidos procedendo ao contrário, separando o código em localização e última letra de forma ordenada. A partir da tabela reconstrói-se a mensagem. Trata-se de um processo não linear cuja análise ultrapassa largamente o objectivo deste capítulo introdutivo à codificação.
Mencione-se no entanto que este algoritmo é hoje em dia o mais utilizado em aplicativos de compressão e descompressão de dados tais como os programas zip e unzip tanto em Unix como em DOS/Windows.
De acordo com o que foi dito anteriormente em relação aos dois tipos de quantificação também aqui podemos distinguir dois tipos de PCM: PCM uniforme e PCM não uniforme. Na PCM uniforme o sinal analógico é primeiramente amostrado a uma taxa superior a Nyquist, i.e., se W
mathend000# for a banda (em Hz) do sinal analógico, a taxa de amostragem deverá ser
fs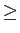 2W
mathend000#. Em seguida o sinal já discreto no tempo é quantificado utilizando 2R
mathend000# níveis discretos entre o valor mínimo e máximo do sinal de entrada
x(t)
2W
mathend000#. Em seguida o sinal já discreto no tempo é quantificado utilizando 2R
mathend000# níveis discretos entre o valor mínimo e máximo do sinal de entrada
x(t) 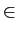 [- xmax, xmax]
mathend000#. Assim o intervalo de quantificação será
[- xmax, xmax]
mathend000#. Assim o intervalo de quantificação será
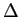 = 2xmax/2R
mathend000#. Aplica-se aqui o que foi dito no caítulo 4.2.1 acerca do ruído de quantificação no caso uniforme.
= 2xmax/2R
mathend000#. Aplica-se aqui o que foi dito no caítulo 4.2.1 acerca do ruído de quantificação no caso uniforme.
A PCM não uniforme difere apenas pelo facto de que antes de ser quantificado, o sinal é filtrado por um elemento não linear destinado a reduzir a sua gama de valores. Na prática isto corresponde a ter mais níveis nos valores em torno a 0 e menos níveis nos valores extremos. Depois desta filtragem em amplitude não linear é aplicada um PCM uniforme. Na recepção, depois de uma descodificação PCM uniforme o sinal deve ser filtrado com um filtro inverso daquele utilizado na transmissão de forma a colocar o sinal na sua gama de valores original. Nas aulas práticas veremos alguns exemplos de filtragem não linear para PCM não uniforme.
Em PCM cada uma das amostras é quantificada e codificada nos 2R
mathend000# bits independentemente das outras amostras anteriores do sinal. Ora na prática, se a taxa de amostragem fs
mathend000# é suficientemente alta, a amplitude do sinal de entrada é suposta não variar muita duma amostra para a seguinte, o que pressupõe a ideia de que em vez de codificar o valor absoluto do sinal a codificação do seu valor em relação à amostra anterior permitiria utilizar muito menos bits e portanto uma menor taxa de transmissão para enviar a mesma quantidade de informação. Esta é a ideia de base do PCM diferencial (DPCM): trata-se de codificar não o valor absoluto do sinal mas apenas a sua variação em relação à amostra anterior. Um dos problemas mais óbvios com a aplicação directa desta ideia simples é de que os erros devidos ao ruído tem tendência para se adicionar ao longo do tempo. Por essa razão surge a ideia de não limitar a dependência da evolução do sinal apenas à última amostra, mas sim às, digamos, p
mathend000# últimas amostras. Assim, constrói-se um modelo de dados recursivo de forma a escrever o sinal amostrado previsto no instante k
mathend000# como
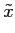 (k) = (k) = 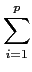 aix(k - i), aix(k - i), |
(4-3.08) |
o que é uma combinação linear ponderada das p
mathend000# amostras anteriores, e onde os coeficientes de ponderação ai
mathend000# são determinados de forma a minimizar o erro quadrático médio
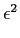 (k)
mathend000# entre o sinal previsto e o sinal real
(k)
mathend000# entre o sinal previsto e o sinal real
E[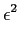 (k)] = E[(xk - (k)] = E[(xk - 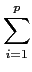 aixk-i)2]. aixk-i)2]. |
(4-3.09) |
Existem vários métodos bem conhecidos para estimar os coeficientes ai
mathend000#, entre os quais os famosos algoritmos de Levison e Durbin (1959). Na prática o que acaba por ter que ser transmitido é o erro entre o sinal predicto e o sinal real o que requer, no lado do receptor, que o mesmo conjunto de coeficientes ai
mathend000# seja utilizado para voltar a reconstruir o sinal x(k)
mathend000# a partir de
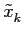 mathend000# e das amostras anteriormente estimadas do sinal. Prova-se que neste algorimo os erros não se acumulam ao longo do tempo.
mathend000# e das amostras anteriormente estimadas do sinal. Prova-se que neste algorimo os erros não se acumulam ao longo do tempo.
Uma das suposições que estão na base do DPCM é que o sinal não muda muito de uma amostra para a seguinte, o que permite obter um bom estimador do seu valor no instante k
mathend000# conhecendo as amostras nos p
mathend000# instantes anteriores. Quanto mais elevado for o valor de p
mathend000# maior é a quantidade de informação reunida no algoritmo para determinar x(k)
mathend000# e normalmente mais estável e preciso será o algoritmo, o que na prática se traduz por uma baixa taxa de erro de transmissão. Porém, não devemos esquecer que na base do método se encontra a suposição de invariabilidade (ou fraca variabilidade temporal) do sinal o que, na presença de ruído, se traduz por estacionaridade. A pergunta que se pode colocar é: então e quando o sinal não é estacionário? A resposta a esta pergunta encontra-se no DPCM adaptativo (ADPCM). Na prática a não estacionaridade é difícil de ter em conta, mas também existem poucos processos de interesse que sejam absolutamente não estacionários e portanto apenas nos interessa o caso da quasi-não estacionaridade, onde a média e a variância variam lentamente com o tempo. Uma das formas para ter em conta esta quasi-não estacionaridade é utilizar um quantificador DPCM uniforme no qual o intervalo de quantificação varia de acordo com a variância local das amostras do sinal de entrada. Por variância local entende-se a variância estimada numa janela temporal em torno à amostra actual. Assim pode-se fazer variar o intervalo de amostragem e portanto a dinâmica do sinal à entrada do quantificador de acordo com as variações lentas do sinal de entrada.
Figura 4.3:
codificação por modulação delta (DM): sistema codificador (a) e sistema descodificador (b).
|
|
A modulação delta (DM) é uma variante simplificada do DPCM e que se encontra representada na figura 4.3. Neste codificador simplificado, o sinal é modelado utilizando um predictor fixo de ordem um (p = 1
mathend000#) do tipo (4-3.8) com a1 = 1
mathend000# e quantificado apenas com um bit (2 níveis). Na prática isto é equivalente a dizer que o valor predicto do sinal é apenas o valor no instante anterior mais o ruído de quantificação. O resultado é que o sinal se encontra aproximado por uma função em escada com um determinado intervalo de quantificação 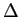 mathend000#. Para ser efectiva, a DM geralmente requere uma taxa de amostragem bem superior a Nyquist, da ordem de 5 vezes a taxa mínima, e que o sinal a emitir evolua lentamente. Mesmo assim existem dois tipos de distorção frequentes no receptor, que são: o erro de ``slope-overload'' e o erro de ruído granular. Estes dois tipos de distorção encontram-se exemplificados na figura 4.4 e resultam, como se pode verificar, de uma demasiado rápida variação da entrada para o intervalo de quantificação, que não consegue acompanhar o sinal, e de uma variação demasiado lenta da entrada que resulta numa constante oscilação em torno a um valor que varia demasiado lentamente.
mathend000#. Para ser efectiva, a DM geralmente requere uma taxa de amostragem bem superior a Nyquist, da ordem de 5 vezes a taxa mínima, e que o sinal a emitir evolua lentamente. Mesmo assim existem dois tipos de distorção frequentes no receptor, que são: o erro de ``slope-overload'' e o erro de ruído granular. Estes dois tipos de distorção encontram-se exemplificados na figura 4.4 e resultam, como se pode verificar, de uma demasiado rápida variação da entrada para o intervalo de quantificação, que não consegue acompanhar o sinal, e de uma variação demasiado lenta da entrada que resulta numa constante oscilação em torno a um valor que varia demasiado lentamente.
Figura 4.4:
distorção de slope overload e ruído granular, devida ao desajuste do intervalo de quantificação.
|
|
Estes dois erros impõem restrições contraditórias no intervalo de quantificação 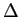 mathend000# que num caso deverá ser maior e no outro caso menor. Existe uma DM com intervalo de quantificação a intervalo variável, na qual
mathend000# que num caso deverá ser maior e no outro caso menor. Existe uma DM com intervalo de quantificação a intervalo variável, na qual 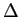 mathend000# é fixado de forma adaptativa de acordo com a maior ou menor taxa de variação do sinal de entrada de forma minimizar simultaneamente os dois tipos de distorção.
mathend000# é fixado de forma adaptativa de acordo com a maior ou menor taxa de variação do sinal de entrada de forma minimizar simultaneamente os dois tipos de distorção.
Devido a estes problemas de sinais com requisitos contraditórios, uns que variam rápido demais e outros lentos demais, colocou-se a ideia de filtrar o sinal a emitir em várias sub-bandas de frequência, podendo assim, eventualmente separar componentes do sinal com maior dinâmica de outros com menor dinâmica, e utilizando mais bits para um e menos para outro. Isto implica uma recombinação do sinal à chegada ao receptor. Demonstrou-se na prática que a codificação em sub-bandas é muito efectiva para a codificação da voz. Assumindo que a voz se encontra entre 0 e 3200 Hz, é frequente definir 4 sub-bandas 0-400, 400-800, 800-1600 e 1600-3200 Hz. Note-se que cada filtro tem uma banda que é o dobro do anterior e são por isso chamados filtros em oitavos de banda. A voz tem geralmente uma dinâmica mais elevada e os erros de quantificação são mais perceptíveis ao ouvido também nessa banda, o que implica que mais bits deverão ser usados para codificar o sinal nas primeiras bandas e progressivamente menos nas seguintes. Geralmente utiliza-se ADPCM em cada sub-banda.
Convém ainda referir, para completar este capítulo, que existe uma outra classe de métodos que tenta resolver o problema da condificação através de um método completamente diferente que é utilizando modelos do sinal. Neste tipo de métodos o que é transmitido deixa de ser o sinal propriamente dito (ou suas componentes) mas sim os coeficientes de um modelo ajustado no sinal. Para certos tipos de sinais, que podem ser correctamente representados pelo modelo utilizado, o ganho em termos de taxa de transmissão e número de bits utilizado pode ser muito superior a qualquer um dos outros métodos de codificação utilizados anteriormente. Um erro de quantificação mínimo é obtido através de um maior ou menor ajuste do modelo e que se traduz por um maior ou menor número de coeficientes. Obviamente que, se o sinal for dificilmente representado pelo modelo, o número de coeficientes necessários para uma representação correcta torna-se muito elevado e devido a limitações práticas no número máximo de coeficientes, a distorção tende a aumentar. Não nos vamos alongar aqui neste tipo de métodos, basta dizer que o mais utilizado se chama codificação de predicção linear (Linear Prediction Coding - LPC), e que passa pela utilização de um modelo auto-regressivo (AR) semelhante ao representado na equação (4-3.8).
Resumo do capítulo 4:
Este capítulo trata dos vários processos por que passa o sinal emitido pela fonte quando da sua entrada no bloco emissor, nomeadamente:
- começa-se por definir uma das grandezas fundamentais em teoria da informação que é precisamente a noção de quantidade de informação. Em particular, diz-se que a quantidade de informação se encontra ligada à entropia e é portanto uma medida do grau de imprevisibilidade da mensagem transmitida;
- estabelece-se a necessidade de quantificar o sinal analógico real num número finito de valores e define-se o ruído de quantificação em função dos vários tipos de quantificadores;
- a codificação da mensagem emitida pela fonte num alfabeto eficiente de transmissão da informação seja com palavras de comprimento fixo seja com palavras de comprimento variável; introduz-se o conceito de eficiência de codificação em relação à entropia teórica. São dados como exemplos o algoritmo de Huffman e o de Lempel-Ziv.
- a codificação de sinais analógicos e o PCM, DPCM, ADPCM e modulação delta são apresentados e caracterizados.
Sergio Jesus
2008-12-30
![]()
![]()
![]()
![]() -
- ![]() =
= ![]()
![]() n
n
![]() = a + (n - 2)
= a + (n - 2)![]() +
+ ![]() ,
,![]() = E[X|X
= E[X|X ![]() Rn]
Rn]
![]() , n
, n ![]() [1, N]
[1, N]
![]()
![]() (k)
(k)
![]() /2,
/2,![]() /2]
/2]
![]() = X/xmax
= X/xmax
![]()
![]()
![]() log2L
log2L
![]() H(x)
H(x)
![]() piNi = 2.21,
piNi = 2.21,![]() H(Xi|X1, X2,..., Xi-1),
H(Xi|X1, X2,..., Xi-1),![]() H(X1, X2,..., Xk).
H(X1, X2,..., Xk).![]()
![]()
![]() Hk(X) =
Hk(X) = ![]()
![]() H(X1, X2,..., Xk).
H(X1, X2,..., Xk).![]() 2W
2W
![]() [- xmax, xmax]
[- xmax, xmax]
![]() = 2xmax/2R
= 2xmax/2R
![]() (k)
(k)
![]()
![\includegraphics[width=12cm]{figs/delta_m.eps}](img238.png)
![]()
![\includegraphics[width=10cm]{figs/erros_DM.eps}](img239.png)
![]()
![]()
![\includegraphics[width=8cm]{figs/entropia_hbp.eps}](img204.png)
![$\displaystyle {{E[X^2]}\over {\epsilon}}$](img208.png) ,
,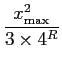 ,
,![$\displaystyle {{E[X^2]} \over {x_{\rm max}^2}}$](img218.png) ]
]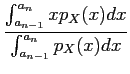
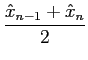 ,
,![\includegraphics[width=10cm]{figs/huffman.eps}](img228.png)