Subsections
Exame de Fundamentos de Telecomunicações - Junho 2004
Problema 1: considere o sinal aleatório
x(t) = A cos(2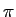 fct +
fct + 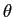 )
mathend000# onde A
mathend000# e fc
mathend000# são duas constantes reais representando respectivamente a amplitude e a frequência do sinal enquanto a fase
)
mathend000# onde A
mathend000# e fc
mathend000# são duas constantes reais representando respectivamente a amplitude e a frequência do sinal enquanto a fase 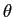 mathend000# é uma variável aleatória, distribuída uniformemente no interval [0, 2
mathend000# é uma variável aleatória, distribuída uniformemente no interval [0, 2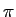 ]
mathend000#.
]
mathend000#.
- a)
- calcule a função de autocorrelação
rxx(t +
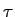 , t)
mathend000# de x(t)
mathend000#
, t)
mathend000# de x(t)
mathend000#
- b)
- determine se x(t)
mathend000# é um processo estacionário. Justifique a sua resposta.
- c)
- calcule a sua densidade espectral de potência
Pxx(f )
mathend000#.
Problema 2: considerando os sinais
{si(t);i = 1,..., 4}
mathend000# da figura F.1, determine
Figura F.1:
sinais
{si(t);i = 1,..., 4}
mathend000#
|
![\includegraphics[width=10cm]{figs/f1_exjun04.eps}](img749.png) |
- a)
- os coeficientes de correlação
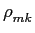 mathend000# entre eles e
mathend000# entre eles e
- b)
- as distâncias euclidianas dmk
mathend000# entre eles.
Problema 3: considere uma sequência discreta sem memória que utiliza um alfabeto de L = 7
mathend000# símbolos
{x1, x2,..., xL}
mathend000# emitidos um em cada milisegundo.
Tabela 6.4:
probabilidade empírica de cada símbolo.
|
| Símbolo |
probabilidade |
| x1
mathend000# |
0.35 |
| x2
mathend000# |
0.30 |
| x3
mathend000# |
0.20 |
| x4
mathend000# |
0.10 |
| x5
mathend000# |
0.04 |
| x6
mathend000# |
0.005 |
| x7
mathend000# |
0.005 |
|
truemm
- a)
- numa primeira transmissão de dados assumiu-se que os símbolos eram equiprováveis. Calcule a entropia da fonte e deduza o número médio de bits necessário para representar cada símbolo do alfabeto durante essa transmissão. Qual a taxa de transmissão em bits/s.
- b)
- utilizando uma codificação com palavras de comprimento fixo, qual o número de bits necessário para representar este alfabeto e qual a taxa de transmissão necessária para transmitir uma mensagem utilizando este tipo de codificação.
- c)
- durante a primeira transmissão fez-se uma estatística da probabilidade de cada símbolo tendo obtido os resultados indicados na tabela 6.4. Qual a entropia efectiva deste alfabeto ?
- d)
- numa segunda transmissão de dados utilizou-se uma codificação com palavras de comprimento variável. Servindo-se do algoritmo de Hauffman determine o código de cada um dos sete símbolos da tabela 6.4.
Exame de Fundamentos de Telecomunicações - Julho 2004
Problema 1: considere um sinal s(t)
mathend000# representado como uma combinação linear de K
mathend000# funções ortonormais fk(t)
mathend000# tal que
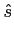
(
t) =
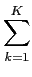 skfk
skfk(
t)
mathend000#
onde
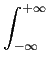 fn
fn(
t)
fm * (
t)
dt =
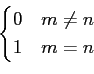
mathend000#
Determine a expressão dos coeficientes
{sk;k = 1,..., K}
mathend000# na expansão
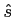 (t)
mathend000# que minimizam a energia
(t)
mathend000# que minimizam a energia
mathend000#
Problema 2: considere uma sequência binária formada por variáveis aleatórias descorrelacionadas de média nula e variância unidade, bn
mathend000#, a partir da qual se formam os símbolos
In = bn + bn-1
mathend000#.
- a)
- demonstre que a função de autocorrelação da sequência de símbolos se escreve
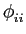
(
m) =
E[
InIn-m] =
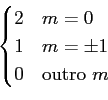
mathend000#
- b)
- calcule a densidade espectral de potência da sequência de símbolos Pii(f )
mathend000#, com uma duração de símbolo de T
mathend000# segundos.
- c)
- se a sequência de símbolos In
mathend000# for transmitida utilizando uma modulação digital com uma forma do pulso
g(t) = u(t) - u(t - T)
mathend000#, onde T
mathend000# é uma constante que representa a duração do pulso e u(t)
mathend000# é a função degrau unidade, calcule a densidade espectral Pss(f )
mathend000# do sinal modulador em banda base slm(t)
mathend000#.
Problema 2: considere uma sequência discreta sem memória que utiliza um alfabeto de L = 6
mathend000# símbolos
{x1, x2,..., xL}
mathend000# emitidos um em cada 3 milisegundos.
Tabela 6.5:
probabilidade empírica de cada símbolo.
|
| Símbolo |
probabilidade |
| x1
mathend000# |
0.30 |
| x2
mathend000# |
0.20 |
| x3
mathend000# |
0.20 |
| x4
mathend000# |
0.20 |
| x5
mathend000# |
0.05 |
| x6
mathend000# |
0.05 |
|
truemm
- a)
- utilizando os resultados indicados na tabela 6.5 calcule a entropia efectiva deste alfabeto ?
- b)
- calcule qual o número de bits mínimo necessário para emitir uma mensagem utilizando este alfabeto codificado utilizando palavras de comprimento fixo. Qual a velocidade de transmissão nesse caso ? Justifique.
- d)
- utilizando uma codificação com palavras de comprimento variável com algoritmo de Hauffman determine o código de cada um dos seis símbolos da tabela 6.5.
Exame de Fundamentos de Telecomunicações I - 2007/08 (normal)
Problema 1 [5 val]: considere o impulso de rádio frequência da figura F.2 na qual uma sinusóide de amplitude A = 2
mathend000# e de frequência fc = 4
mathend000# kHz se encontra modulada por uma função porta simétrica de amplitude unitária e de duração T = 1
mathend000# ms.
Figura F.2:
impulso de rádio frequência.
|
![\includegraphics[width=10cm]{figs/f1_exfdt0708.eps}](img754.png) |
- a)
- [1v] escreva a expressão do sinal s(t)
mathend000# para qualquer t
mathend000#,
- b)
- [1v] calcule a sua Transformada de Fourier S(f )
mathend000#,
- c)
- [2v] represente o espectro de amplitude e o espectro de fase do sinal s(t)
mathend000#.
- d)
- [1v] calcule o valor aproximado da largura de banda a -3 dB do espectro de potência deste impulso ?
Problema 2 [8 val]: um canal de transmissão tem uma resposta y(t)
mathend000# a um sinal de entrada x(t)
mathend000#, tal que
y(
t) =
k1x(
t -
t1) +
k2x(
t -
t2)

(1)
mathend000#
onde k1, k2
mathend000# são constantes < 1
mathend000# e t2 > t1
mathend000#.
- a)
- [1v] escreva a resposta impulsiva hc(t)
mathend000# do canal de transmissão.
- b)
- [1v] calcule a sua resposta em frequência
Hc(f )= Y(f )/X(f )
mathend000#.
- c)
- [1v] sabendo que um sinal é dito sem distorção se
z(t) = k0x(t - t0)
mathend000#, onde k0
mathend000# e t0
mathend000# são constantes, determine
H(f )= Z(f )/X(f )
mathend000#.
- d)
- [3v] com o objectivo de igualizar o canal de transmissão coloca-se um igualizador de função de transferência Heq(f )
mathend000# em cascata com o canal Hc(f )
mathend000#, tal que a função de transferência total se escreve
H(f )= Hc(f )Heq(f )
mathend000#. Fazendo k0 = k1
mathend000#, t0 = t1
mathend000# e aproximando
mathend000#
calcule a expressão aproximada do igualizador Heq(f )
mathend000# que permite obter à saída do conjunto canal-igualizador um sinal z(t)
mathend000# sem distorção.
- e)
- [2v] determine a resposta impulsiva do igualizador heq(t)
mathend000#.
Problema 3 [7 val]: considere o seguinte sinal
s(
t) =
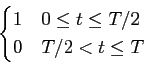
mathend000#
- a)
- [1v] escreva a resposta impulsiva h(t)
mathend000# do filtro adaptado ao sinal s(t)
mathend000#.
- b)
- [2v] sabendo que o receptor óptimo se obtem como a saída do filtro adaptado deslocado da duração T
mathend000# do sinal, calcule e represente a resposta r(t)
mathend000# do filtro adaptado ao sinal s(t)
mathend000#. Determine o valor máximo da saída r(t)
mathend000# e para que instante esse valor é obtido.
- c)
- [3v] se o sinal y(t)
mathend000# à entrada do filtro adaptado tiver ruído,
y(t) = s(t) + n(t)
mathend000#, onde n(t)
mathend000# é um ruído branco, gaussiano de média nula e de variância
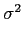 mathend000#, calcule E[r(T)]
mathend000# e V[r(T)]
mathend000#.
mathend000#, calcule E[r(T)]
mathend000# e V[r(T)]
mathend000#.
- d)
- [1v] escreva a expressão da densidade de probabilidade de r(T)
mathend000#.
Exame de Fundamentos de Telecomunicações I - 2007/08 (recurso)
Problema 1 [7 val]: considere um canal de transmissão com a seguinte resposta em frequência (amplitude)
|
B(
f )|=
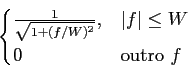
mathend000#
onde W = 4800
mathend000# Hz é a sua largura de banda e com ruído aditivo, Gaussiano de média nula e de densidade espectral N0/2
mathend000#. Este canal é utilizado para transmitir dados binários a uma taxa de 4800 bits/s.
- a)
- [3v] determine uma forma de pulso g(t)
mathend000# que permita obter ISI nulo.
- b)
- [4v] determine o espectro de amplitude do filtro emissor e do filtro receptor de forma a obter uma transmissão de dados óptima neste canal.
Problema 2 [10 val]: a resposta em frequência de um canal passa baixo é dada por
H(
f )=
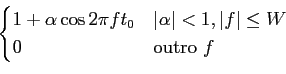
mathend000#
onde W
mathend000# é a largura de banda do canal. Um sinal s(t)
mathend000# de banda inferior a W
mathend000# é passado através do canal.
- a)
- [3v] demonstre que o sinal de saída se escreve
y(t) = s(t) + (
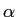 /2)[s(t - t0) + s(t + t0)]
mathend000#
/2)[s(t - t0) + s(t + t0)]
mathend000#
- b)
- [3v] sabendo que o sinal y(t)
mathend000# é passado através de um filtro adaptado ao sinal s(t)
mathend000#, determine a resposta r(t)
mathend000# do filtro nos instantes t = kT
mathend000#, para
k = 0,
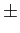 1,
1,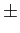 2
mathend000#, onde T
mathend000# é o intervalo do símbolo.
2
mathend000#, onde T
mathend000# é o intervalo do símbolo.
- c)
- [4v] defina o valor da interferência intersimbólica quando t0 = T
mathend000# ?
Problema 3 [3 val]: demonstre que
x(t) = (- 1/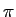 t) *
t) * 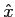 (t)
mathend000#, onde
(t)
mathend000#, onde 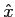 (t)
mathend000# é a Transformada de Hilbert de x(t)
mathend000#.
(t)
mathend000# é a Transformada de Hilbert de x(t)
mathend000#.
Exame de Fundamentos de Telecomunicações I - 2008/09 (normal)
Problema 1 [6 val]: considere o sinal modulado por impulsos de amplitude (ASK)
s(
t) =
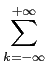 Akg
Akg(
t -
kTs)
mathend000#
onde g(t)
mathend000# é a forma de pulso e onde o intervalo de símbolo Ts = 1
mathend000# ms.
- a)
- [1v] qual a taxa de transmissão de símbolo Rs
mathend000# ? E a taxa de transmissão de bit Rb
mathend000# com M=2 ? E para M=16 ? Justifique as suas respostas.
- b)
- [2v] para uma forma de pulso rectangular de amplitude unidade determine a densidade espectral de potência Ps(f )
mathend000# de s(t)
mathend000# quando a sequência aleatória Ak
mathend000# é estacionária, sem memória, de média nula e de variância
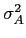 mathend000#.
mathend000#.
- c)
- [2v] represente Ps(f )
mathend000# calculado em b) e calcule o valor aproximado da largura de banda a -3 dB.
- d)
- [1v] assumindo que o sinal s(t)
mathend000# é enviado através de um canal de transmissão cuja resposta em frequência em banda base é constante numa banda [- W, W]
mathend000#, determinar a condição em T
mathend000# para que o sinal recebido tenha ISI nula (``zero forcing''), desprezando a energia fora da banda a -3 dB da densidade espectral de s(t)
mathend000#.
Problem 2 [7 val]: consider the set of signals
{si(t);i = 1,..., 4;0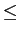 t
t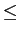 3}
mathend000# of figure F.3.
3}
mathend000# of figure F.3.
Figura F.3:
signals
{si(t);i = 1,..., 4}
mathend000#
|
![\includegraphics[width=10cm]{figs/f1_exdec08.eps}](img759.png) |
- a)
- [1v] calculate the energy
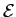 i
mathend000# of each one of the signals si(t)
mathend000#
i
mathend000# of each one of the signals si(t)
mathend000#
- b)
- [1v] determine and represent the energy normalized set of signals
{
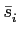 (t)}
mathend000#.
(t)}
mathend000#.
- c)
- [2v] calculate the correlation coefficients between signals,
{
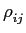 ;i, j = 1,..., 4, i
;i, j = 1,..., 4, i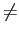 j}
mathend000#. The proposed set of signals may form an orthogonal/orthonormal basis functions? Justify your answer.
j}
mathend000#. The proposed set of signals may form an orthogonal/orthonormal basis functions? Justify your answer.
- d)
- [2v] from the same set of signals form an orthonormal basis of functions. What's the dimension of that basis ? Justify.
- e)
- [1v] let us assume that we want to transmit the following signal s(t)
mathend000#
s(
t) =
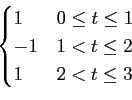
mathend000#
Determine the coefficients sk
mathend000# of the expansion of s(t)
mathend000# in the orthonormal basis determined in d) such that
mathend000#
where K
mathend000# is the dimension of the basis also determined in d). Is this basis of signals complete ? Justify.
Problema 3 [7 val]: considere o seguinte sinal
s(
t) =
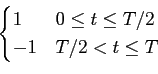
mathend000#
- a)
- [1v] escreva a resposta impulsiva h(t)
mathend000# do filtro adaptado ao sinal s(t)
mathend000#.
- b)
- [2v] sabendo que o receptor óptimo se obtém como a saída do filtro adaptado deslocado da duração T
mathend000# do sinal, calcule e represente a resposta r(t)
mathend000# do filtro adaptado ao sinal s(t)
mathend000#.
- c)
- [1v] determine o valor máximo da saída r(t)
mathend000# e para que instante esse valor é obtido.
- d)
- [2v] se o sinal y(t)
mathend000# à entrada do filtro adaptado tiver ruído,
y(t) = s(t) + n(t)
mathend000#, onde n(t)
mathend000# é um ruído branco, gaussiano de média nula e de variância
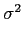 mathend000#, calcule E[r(t)]
mathend000# e V[r(t)]
mathend000#, respectivamente valor esperado e variância da resposta do filtro adaptado.
mathend000#, calcule E[r(t)]
mathend000# e V[r(t)]
mathend000#, respectivamente valor esperado e variância da resposta do filtro adaptado.
- e)
- [1v] no caso do sinal de entrada do filtro adaptado com ruído, escreva a expressão da densidade de probabilidade de r(T)
mathend000#.
Sergio Jesus
2008-12-30
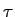 , t)
, t)
![]()
![]() (t) =
(t) = ![]() skfk(t)
skfk(t)
![]() fn(t)fm * (t)dt =
fn(t)fm * (t)dt = 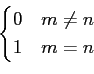
![]() (t)
(t)
![]() =
= ![]() |s(t) -
|s(t) - ![]() (t)
(t)![]() dt
dt
![]() (m) = E[InIn-m] =
(m) = E[InIn-m] = 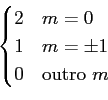
![]() (1)
(1)
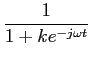
![]() 1 - ke-j
1 - ke-j![]() t
t
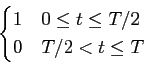
![]()
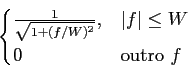
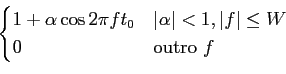
![]() /2)[s(t - t0) + s(t + t0)]
/2)[s(t - t0) + s(t + t0)]
![]() 1,
1,![]() 2
2
![]() t) *
t) * ![]() (t)
(t)
![]() (t)
(t)
![]() Akg(t - kTs)
Akg(t - kTs)
![]()
![]() t
t![]() 3}
3}
![]() i
i
![]() (t)}
(t)}
![]() ;i, j = 1,..., 4, i
;i, j = 1,..., 4, i![]() j}
j}
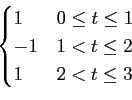
![]() sk
sk![]() (t), 0
(t), 0![]() t
t![]() 3
3
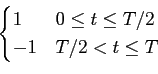
![]()
![\includegraphics[width=10cm]{figs/f1_exjun04.eps}](img749.png)
![\includegraphics[width=10cm]{figs/f1_exfdt0708.eps}](img754.png)
![\includegraphics[width=10cm]{figs/f1_exdec08.eps}](img759.png)