| pX(x) | = | 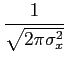 e e |
|
| pY(y) | = | 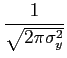 e e |
podemos então obter a densidade de proabilidade de Z
No caso em que mx = my = 0
e dado que
| E[Z] | = | E[X] + jE[Y] | |
| V[Z] | = | E[|Z - E[Z] |
|
| = | E[|Z |
||
| = | V[X] + V[Y] | ||
| = | 2 |
e assim
truemm
Sergio Jesus 2008-12-30
Considere-se uma varável aleatória Gaussiana complexa Z = X + jY
truemm
![]()
![]()
pX(x)
=
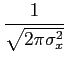 e
e![]()
pY(y)
=
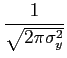 e
e![]()
podemos então obter a densidade de proabilidade de Z
No caso em que mx = my = 0
![]() =
= ![]() =
= ![]()
e dado que
E[Z]
=
E[X] + jE[Y]
V[Z]
=
E[|Z - E[Z]
![]() ]
]
=
E[|Z
![]() ] -|E[Z]
] -|E[Z]![]()
=
V[X] + V[Y]
=
2
![]()
e assim
![]() = 2
= 2![]()
Sergio Jesus
2008-12-30