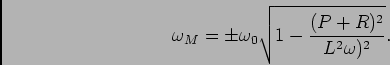Next: Trabalho prático
Up: Filtro RLC em regime
Previous: Filtro RLC em regime
Contents
- a)
- b)
- c)
- derivando
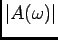 temos que
temos que
Igualando a zero temos que
ou ainda que a frequência do máximo da curva de amplitude é
O valor limite do potenciómetro 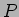 deduz-se do radicando da expressão acima assumindo que quando este se torna negativo deixa de haver sobretensão.
deduz-se do radicando da expressão acima assumindo que quando este se torna negativo deixa de haver sobretensão.
o que nos permite calcular
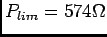 .
.
- d)
- com
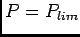 temos o caso ao limite da sobretensão. Na prática a caurva admite uma assímptota para 0 dB quando
temos o caso ao limite da sobretensão. Na prática a caurva admite uma assímptota para 0 dB quando 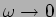 e uma assímptota de -20 dB por decada quando
e uma assímptota de -20 dB por decada quando
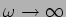 .
.
Sergio Jesus
2003-12-07
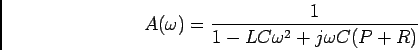
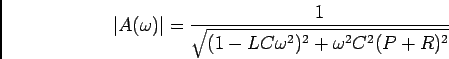
![\begin{displaymath}{{d \vert A(\omega)\vert}\over {d\omega}} =
{{-1/2[2(1-LC\ome...
...2(P+R)^2}\over
{[(1-LC\omega^2)^2+\omega^2 C^2(P+R)^2]^{-3/2}}}\end{displaymath}](img1672.png)
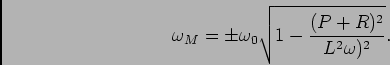

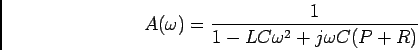
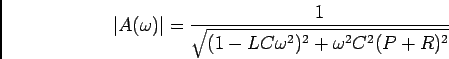
![\begin{displaymath}{{d \vert A(\omega)\vert}\over {d\omega}} =
{{-1/2[2(1-LC\ome...
...2(P+R)^2}\over
{[(1-LC\omega^2)^2+\omega^2 C^2(P+R)^2]^{-3/2}}}\end{displaymath}](img1672.png)